码农场
“一切只贴公式不写代码的博客都是在耍流氓”——图灵·佳德。本文对应《统计学习方法》第3章，用数十行代码实现KNN的kd树构建与搜索算法，并用matplotlib可视化了动画观赏。
k近邻算法
给定一个训练数据集，对新的输入实例，在训练数据集中找到跟它最近的k个实例，根据这k个实例的类判断它自己的类（一般采用多数表决的方法）。
k近邻模型
模型有3个要素——距离度量方法、k值的选择和分类决策规则。
模型
当3要素确定的时候，对任何实例（训练或输入），它所属的类都是确定的，相当于将特征空间分为一些子空间。
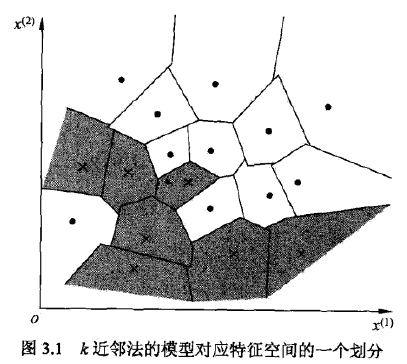
距离度量
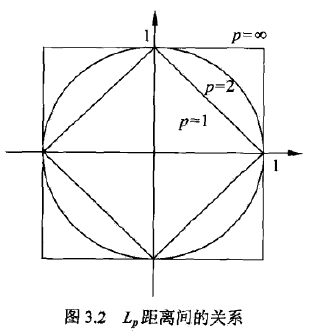
对n维实数向量空间Rn，经常用Lp距离或曼哈顿Minkowski距离。
Lp距离定义如下：
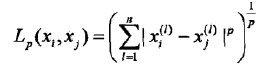
当p=2时，称为欧氏距离：
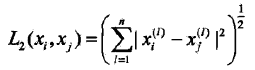
当p=1时，称为曼哈顿距离：
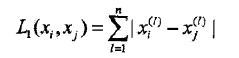
当p=∞，它是各个坐标距离的最大值，即：
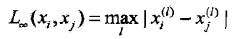
用图表示如下：
k值的选择
k较小，容易被噪声影响，发生过拟合。
k较大，较远的训练实例也会对预测起作用，容易发生错误。
分类决策规则
使用0-1损失函数衡量，那么误分类率是：
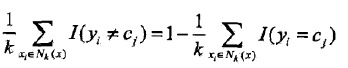
Nk是近邻集合，要使左边最小，右边的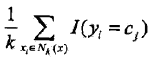
必须最大，所以多数表决=经验最小化。
k近邻法的实现：kd树
算法核心在于怎么快速搜索k个近邻出来，朴素做法是线性扫描，不可取，这里介绍的方法是kd树。
构造kd树
对数据集T中的子集S初始化S=T，取当前节点node=root取维数的序数i=0，对S递归执行：
找出S的第i维的中位数对应的点，通过该点，且垂直于第i维坐标轴做一个超平面。该点加入node的子节点。该超平面将空间分为两个部分，对这两个部分分别重复此操作（S=S'，++i，node=current），直到不可再分。
例子
Python代码
短短几行即可搞定：
T = [[2, 3], [5, 4], [9, 6], [4, 7], [8, 1], [7, 2]] class node: def __init__(self, point): self.left = None self.right = None self.point = point pass def median(lst): m = len(lst) / 2 return lst[m], m def build_kdtree(data, d): data = sorted(data, key=lambda x: x[d]) p, m = median(data) tree = node(p) del data[m] print data, p if m > 0: tree.left = build_kdtree(data[:m], not d) if len(data) > 1: tree.right = build_kdtree(data[m:], not d) return tree kd_tree = build_kdtree(T, 0) print kd_tree
可视化
可视化的话则要费点功夫保存中间结果，并恰当地展示出来
# -*- coding:utf-8 -*-
# Filename: kdtree.py
# Author：hankcs
# Date: 2015/2/4 15:01
import copy
import itertools
from matplotlib import pyplot as plt
from matplotlib.patches import Rectangle
from matplotlib import animation
T = [[2, 3], [5, 4], [9, 6], [4, 7], [8, 1], [7, 2]]
def draw_point(data):
X, Y = [], []
for p in data:
X.append(p[0])
Y.append(p[1])
plt.plot(X, Y, 'bo')
def draw_line(xy_list):
for xy in xy_list:
x, y = xy
plt.plot(x, y, 'g', lw=2)
def draw_square(square_list):
currentAxis = plt.gca()
colors = itertools.cycle(["r", "b", "g", "c", "m", "y", '#EB70AA', '#0099FF'])
for square in square_list:
currentAxis.add_patch(
Rectangle((square[0][0], square[0][1]), square[1][0] - square[0][0], square[1][1] - square[0][1],
color=next(colors)))
def median(lst):
m = len(lst) / 2
return lst[m], m
history_quare = []
def build_kdtree(data, d, square):
history_quare.append(square)
data = sorted(data, key=lambda x: x[d])
p, m = median(data)
del data[m]
print data, p
if m >= 0:
sub_square = copy.deepcopy(square)
if d == 0:
sub_square[1][0] = p[0]
else:
sub_square[1][1] = p[1]
history_quare.append(sub_square)
if m > 0: build_kdtree(data[:m], not d, sub_square)
if len(data) > 1:
sub_square = copy.deepcopy(square)
if d == 0:
sub_square[0][0] = p[0]
else:
sub_square[0][1] = p[1]
build_kdtree(data[m:], not d, sub_square)
build_kdtree(T, 0, [[0, 0], [10, 10]])
print history_quare
# draw an animation to show how it works, the data comes from history
# first set up the figure, the axis, and the plot element we want to animate
fig = plt.figure()
ax = plt.axes(xlim=(0, 2), ylim=(-2, 2))
line, = ax.plot([], [], 'g', lw=2)
label = ax.text([], [], '')
# initialization function: plot the background of each frame
def init():
plt.axis([0, 10, 0, 10])
plt.grid(True)
plt.xlabel('x_1')
plt.ylabel('x_2')
plt.title('build kd tree (www.hankcs.com)')
draw_point(T)
currentAxis = plt.gca()
colors = itertools.cycle(["#FF6633", "g", "#3366FF", "c", "m", "y", '#EB70AA', '#0099FF', '#66FFFF'])
# animation function. this is called sequentially
def animate(i):
square = history_quare[i]
currentAxis.add_patch(
Rectangle((square[0][0], square[0][1]), square[1][0] - square[0][0], square[1][1] - square[0][1],
color=next(colors)))
return
# call the animator. blit=true means only re-draw the parts that have changed.
anim = animation.FuncAnimation(fig, animate, init_func=init, frames=len(history_quare), interval=1000, repeat=False,
blit=False)
plt.show()
anim.save('kdtree_build.gif', fps=2, writer='imagemagick')
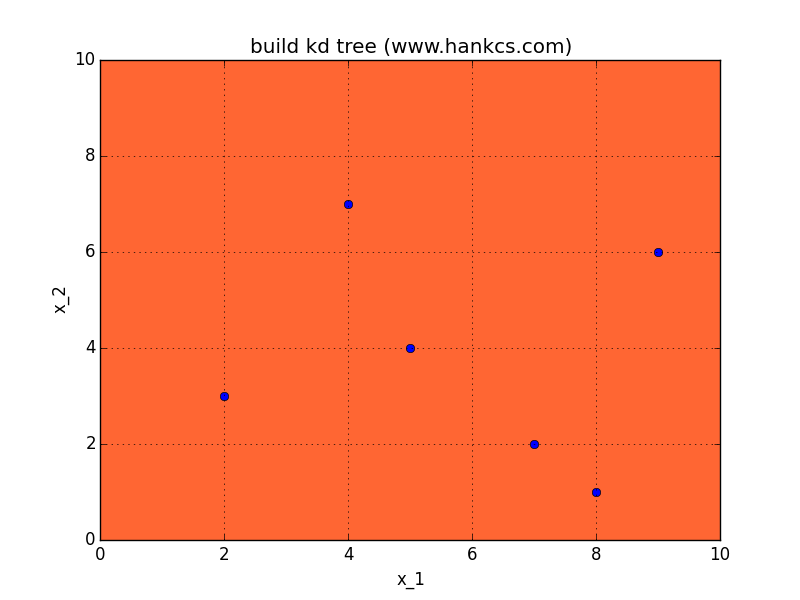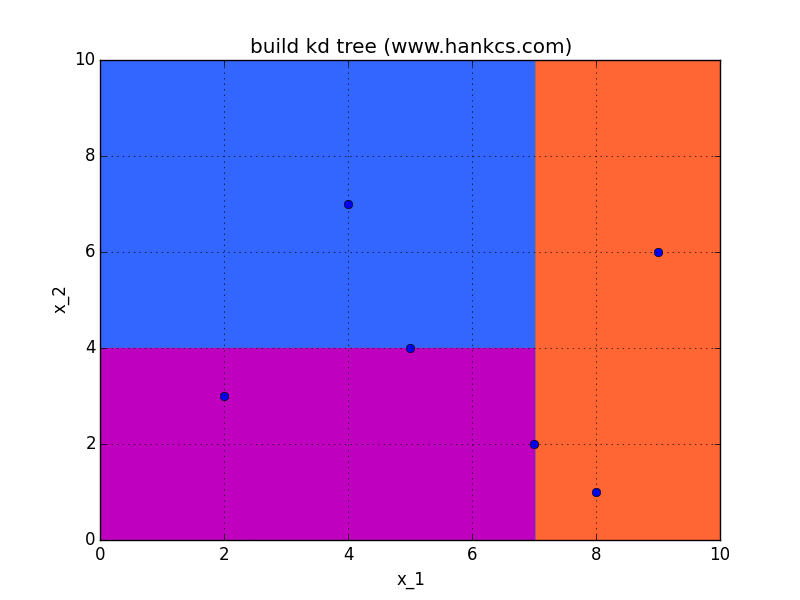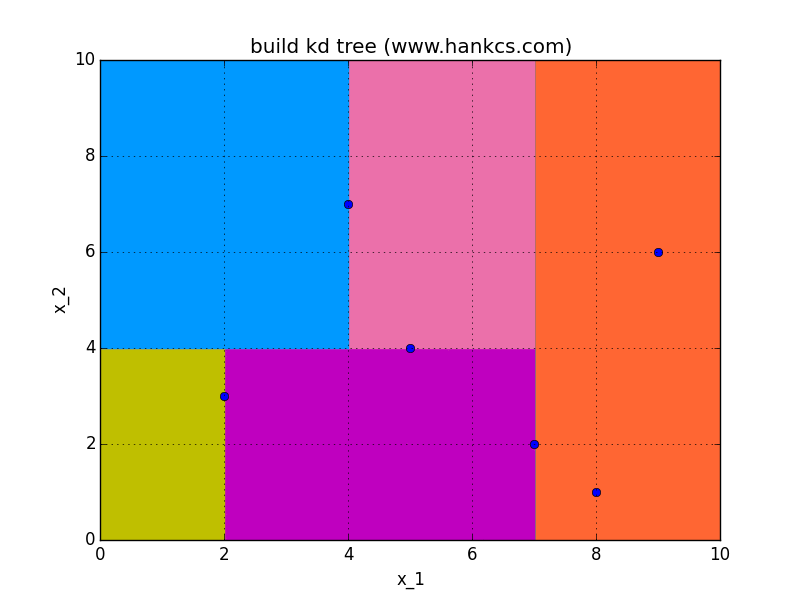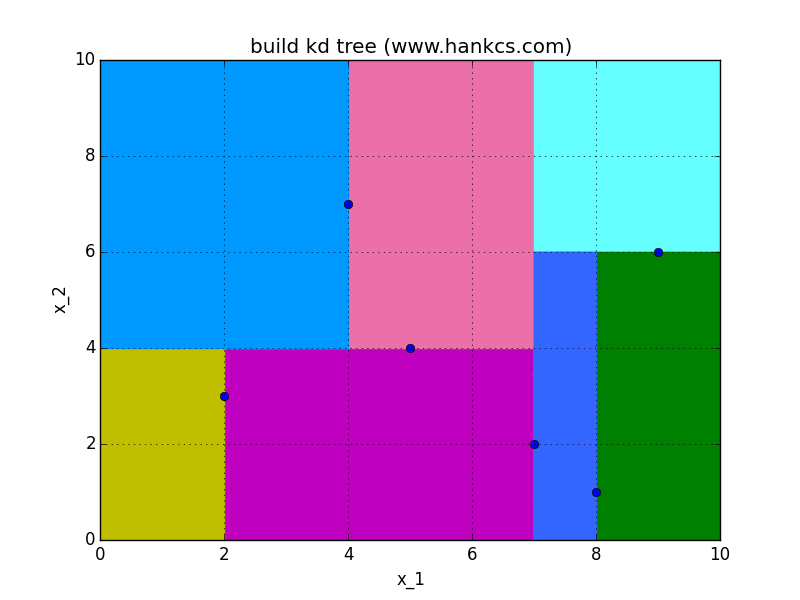
搜索kd树
上面的代码其实并没有搜索kd树，现在来实现搜索。
搜索跟二叉树一样来，是一个递归的过程。先找到目标点的插入位置，然后往上走，逐步用自己到目标点的距离画个超球体，用超球体圈住的点来更新最近邻（或k最近邻）。以最近邻为例，实现如下（本实现由于测试数据简单，没有做超球体与超立体相交的逻辑）：
# -*- coding:utf-8 -*- # Filename: search_kdtree.py # Author：hankcs # Date: 2015/2/4 15:01 T = [[2, 3], [5, 4], [9, 6], [4, 7], [8, 1], [7, 2]] class node: def __init__(self, point): self.left = None self.right = None self.point = point self.parent = None pass def set_left(self, left): if left == None: pass left.parent = self self.left = left def set_right(self, right): if right == None: pass right.parent = self self.right = right def median(lst): m = len(lst) / 2 return lst[m], m def build_kdtree(data, d): data = sorted(data, key=lambda x: x[d]) p, m = median(data) tree = node(p) del data[m] if m > 0: tree.set_left(build_kdtree(data[:m], not d)) if len(data) > 1: tree.set_right(build_kdtree(data[m:], not d)) return tree def distance(a, b): print a, b return ((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2) ** 0.5 def search_kdtree(tree, d, target): if target[d] < tree.point[d]: if tree.left != None: return search_kdtree(tree.left, not d, target) else: if tree.right != None: return search_kdtree(tree.right, not d, target) def update_best(t, best): if t == None: return t = t.point d = distance(t, target) if d < best[1]: best[1] = d best[0] = t best = [tree.point, 100000.0] while (tree.parent != None): update_best(tree.parent.left, best) update_best(tree.parent.right, best) tree = tree.parent return best[0] kd_tree = build_kdtree(T, 0) print search_kdtree(kd_tree, 0, [9, 4])
去掉注释和空白，大概数十行，Python真不愧是可运行的伪码。
输出：
[8, 1] [9, 4] [5, 4] [9, 4] [9, 6] [9, 4] [9, 6]
可见对于点[9, 4]，在n=6的数据集中，kdtree算法一共只进行了3次计算。
算法的回溯过程应该有问题， 我在该代码基础上做了一定的修改：http://blog.csdn.net/castle_cc/article/details/78851154
search_kdtree的实现有问题，仅仅对每个父节点的左右子节点比较并不能完全确定最近临的节点
我自己用500行C代码实现了k-d tree，特点是可以指定任意样本维度以及K数值：https://github.com/begeekmyfriend/kdtree
build_kdtree的第22行，"not d"，我的输出是False or True，我的python版本是2.7.6。
改成
dim = len(data[0])
if m > 0: tree.left = build_kdtree(data[:m], (d+1)%dim)，
是不是更好一些呀？
楼主，我觉得在搜索kd树那块代码中，build_kdtree函数中不需要del date[m]，比如当你目标点是[7,2]的时候就会有不一样的结果
没有做超球体与超立体相交的逻辑，这样岂不是就跟线性扫描是一个复杂度了
效果很棒，哈哈~
上外的妹子麽？
高校学生一枚，个人主页，http://simbazz.info
看了你的部分博文，对机器学习啥的挺感兴趣，
微信 Q289192220，求交流~
贴公式还写代码的博客
写的很好，赞一个
这个多说老是挂掉，他们的服务器太不稳定，太影响我表达对楼主的敬仰之情了！
过奖了，多说的确不稳定。