![]()

细菌繁殖:x个细菌一小时后繁殖为xx个,求A个细菌B小时后的数量模C的余?
输入格式:第一行为整数T,代表T个测试用例。接着是T行,每行3个整数,代表A B C。其中数据范围如下——
1 ≤ T ≤ 500
1 ≤ A ≤ 1000
1 ≤ C ≤ 1000
Small
1 ≤ B ≤ 2
Large
1 ≤ B ≤ 1000
输出格式:Case #X: N,X为用例ID,N为答案。示例如下——
输入
输出 5
1 10 997
2 2 997
2 2 6
461 1 709
461 1000 709Case #1: 1
Case #2: 256
Case #3: 4
Case #4: 674
Case #5: 461
4.1更加复杂的数学问题
模运算的世界
有两个月没刷题了,智商完全下线了。这是Google Code Jam Japan 2011决赛的题目B,一开始想当然地以为可以先求余再迭代,大错特错。无奈看了官方的解说,才明白是怎么回事。
定义n小时后细菌的数量为an,记bn,m=an % m。那么题目就是求 bB,C 。
根据细菌的性质,有

虽然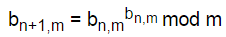 并不成立,但是如下关系是成立的:
并不成立,但是如下关系是成立的:

因为等式右边残留着an 所以无法递推 bn,m 。与其直接考虑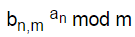 ,不如将指数 an 换为0、1、2……来观察有没有规律。取 bn,m = 14, m = 24 ,计算 bn,m0 mod m , bn,m1 mod m , … 有:
,不如将指数 an 换为0、1、2……来观察有没有规律。取 bn,m = 14, m = 24 ,计算 bn,m0 mod m , bn,m1 mod m , … 有:

除了开头三个数之外,接下来都是8和16的循环节。记循环节「 8, 16, … 」周期为p,开头不规则的部分「 1, 14, 4 」长度为q,给定 bn,m 和 m 就能将p和q算出来,因为m最大1000,顶多循环1000次。
那么接下来在考虑an,an也是个大数,无法直接计算。既然一个数的幂乘的余后半部分一定是循环的,那么只要知道an是否位于循环节中,以及an % p就行了。前者很简单,而后者就是bn,p。
到此为止,就可以用 bn,m , bn,p 将 bn+1,m 表示出来了,这是一个递归的求法。由于n和p的取值在1000*1000之内,所以可以将其枚举出来,之后直接从dp cache里取答案的话就能在有限时间内算完large了。
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAX_N = 1000;
const LL INF = 10000;
// 二维数组[i][j]表示组合i^n % j (n=0,1,2...)
int q[MAX_N + 1][MAX_N + 1]; // 组合对应的非循环节的长度
int p[MAX_N + 1][MAX_N + 1]; // 组合对应的循环节的长度
int dp[MAX_N + 1][MAX_N + 1]; // dp[b][c] := A固定、B为b、C为c时的答案
int an[MAX_N + 1]; // an[i] = A^A迭代i次
// 初始化组合的循环节软cache
void init()
{
int used[MAX_N + 1]; // 记录当前值是否出现过,对应其在第几次计算时出现
for (int i = 1; i <= MAX_N; ++i) // 计算bn,m^[0,1,2...]对应的p、q
{
for (int j = 1; j <= MAX_N; ++j)
{
memset(used, -1, sizeof(used));
int step = 0;
int x = 1;
while (1)
{
x = x * i % j;
if (used[x] >= 0)
{
q[i][j] = used[x];
p[i][j] = step - used[x];
break;
}
used[x] = step++;
}
}
}
}
// return (a ^ b) % mod
LL power(LL x, LL b, LL mod)
{
LL ret = 1LL;
while (b > 0)
{
if (b & 1)
ret = ret * x % mod;
x = x * x % mod;
b >>= 1;
}
return ret;
}
// return min(INF, x^b)
LL power(LL x, LL b)
{
LL ret = 1LL;
while (b > 0)
{
if (b & 1)
ret = min(INF, ret * x);
x = min(INF, x * x);
b >>= 1;
}
return ret;
}
// return x^x迭代b次后除以mod的余数
int rec(int x, int b, int mod)
{
if (!b) return x % mod; // 不繁殖
if (mod == 1) return 0;
if (dp[b][mod] >= 0) return dp[b][mod]; // 在递归过程中已经计算过
int y = rec(x, b - 1, mod); // 往前递归,求出b[n-1][m]
if (!y)
return dp[b][mod] = 0; // i^n % j,当i=0的时候,当然为0
int head = q[y][mod];
int loop = p[y][mod];
int ret;
if (an[b - 1] <= head) // 循环节之外
ret = power(y, an[b - 1], mod);
else // 循环节之内
{
int z = rec(x, b - 1, loop); // a[n-1]%p
z = ((z - (head + 1)) % loop + loop) % loop + 1 + head; // 由于循环节是从head开始的,需要减掉这个head求余之后加回来
ret = power(y, z, mod); // b[n-1][m]^(a[n-1]) % m
}
return dp[b][mod] = ret;
}
void solve()
{
int T;
cin >> T;
for (int i = 0; i < T; ++i)
{
int A, B, C;
cin >> A >> B >> C;
an[0] = A;
for (int j = 1; j <= MAX_N; ++j)
{
an[j] = power(an[j - 1], an[j - 1]);
}
memset(dp, -1, sizeof(dp));
int ret = rec(A, B, C);
cout << "Case #" << i + 1 << ": " << ret << endl;
}
}
///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
freopen("B-large-practice.in", "r", stdin);
freopen("out.txt", "w", stdout);
init();
solve();
fclose(stdin);
fclose(stdout);
system("out.txt");
return 0;
}
///////////////////////////End Sub//////////////////////////////////
Reference
https://code.google.com/codejam/contest/dashboard?c=1363489#s=a&a=1
http://techtipshoge.blogspot.com/2012/04/google-code-jam-japan-2011.html
 码农场
码农场