
递归函数:定义函数
其中 {ai} = {1, 2, …, d-1} and {bi} = {0, 1, …, d-1}
定义递归形式
现给出方程
求最小非负解x。
4.1更加复杂的数学问题
模运算的世界
没有数论的背景知识真的做不来这题。查了书,查了wiki,从倒闭的百度空间的Google cache里抢救了一篇题解回来(真讽刺),加入了自己的注释,这才弄明白是怎么回事。
首先,如果将m写成d进制:
(rk, r(k – 1), r(k – 2), …, r3, r2, r1, r0)
ri代表从低位到高位的第i位,那么有
f(m) = (a(rk), b(r(k – 1)), b(r(k – 2)), …, b(r3), b(r2), b(r1), b(r0))
具体证明见《具体数学》P16:
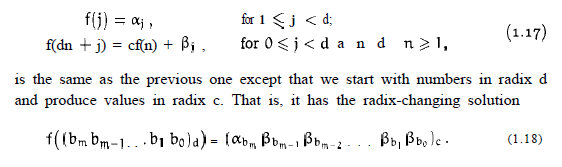
也就是说,除了最高位之外,其余各位都是用数组b置换,而最高位是用数组a置换的。所谓置换,就是从第一次开始,直接拿第i位去数组a或b中去取出相应下标的值作为第i位,下一次迭代也是如此。
所以,如果m和k在d进制下的位数不相等,那么肯定无解,因为m无论怎么变,位数是不会改变的。
然后问题就转化成了变化多少次能够让m的每一位都变成k。现在各位之间是没有什么关系的,我们干脆一位一位地考虑。
对于d进制数字m和k中的任意同一位的两个数,我们得想办法让它们置换到相等。
由于a和b是置换,如果两个数在一个圈里,就一定能在有限步内由一个数变成另外一个数,反之就永远变不成。并且如果圈的大小为R,第一次能变成的步数为C,必然有0≤C<R,并且能够变成的步数集合就是模R的剩余类C。
依次处理每一位,就能列出一系列的线性同余方程。这个线性同余方程组的最小解就是原问题的答案。然而,每个方程取模的底数不一定是互素的,所以我们不能简单套用中国剩余定理。
为了简化起见考虑只有两个方程的情况:
x ≡ c1 (mod r1)
x ≡ c2 (mod r2)
c为第一次能变成的步数,r为圈的大小。
不妨设x = k1 * r1 + c1 = k2 * r2 + c2。变形之后有
c1 – c2 = k2 * r2 – k1 * r1
由裴蜀定理,这个方程有解的充要条件是(c1 – c2)是r1, r2最大公约数d的倍数。求解的话用扩展欧几里得算法即可。
那么原来的那一大堆方程又怎么办呢?我们可以把两个方程化成一个方程,对于上面的两个方程,如果一个可行解是x0,那么它的解集与下面的方程是相同的:
x ≡ x0 (mod [r1, r2])
其中[r1, r2] = lcm(r1, r2),也就是r1与r2的最小公倍数。这样联立方程组的时候,只要从第二个开始,合并前一个得到一个新方程,然后不断地加入新方程即可。这样一个循环就能将所有的方程联立起来。
#include <iostream>
using namespace std;
typedef long long LL;
// 大数类
class bign
{
#define base 1000
#define digit 3
private:
int _arr[110];
int _m;
void bign::_simplify(void)
{
for (int i = 0; i <= _m; i++)
{
if (i == _m && _arr[i] >= base) _m++;
_arr[i + 1] += _arr[i] / base;
_arr[i] %= base;
}
}
public:
bign::bign(void) : _m(0) { memset(_arr, 0, sizeof(_arr)); }
bign::bign(int init) : _m(0)
{
memset(_arr, 0, sizeof(_arr));
_arr[0] = init;
_simplify();
}
friend istream& operator >> (istream& fin, bign& a)
{
char init[10010]; int len, b, t;
fin >> init;
len = strlen(init); a._m = -1;
for (int i = len - 1; i >= 0;)
{
t = 0, b = 1;
for (int j = 0; j < digit && i >= 0; j++, i--)
{
t += (init[i] - '0') * b;
b *= 10;
}
a._arr[++a._m] = t;
}
return fin;
}
friend bign operator / (bign a, int b)
{
for (int i = a._m; i >= 0; i--)
{
if (a._arr[i] < b && i == a._m && i != 0) a._m--;
if (i > 0) a._arr[i - 1] += (a._arr[i] % b) * base;
a._arr[i] /= b;
} return a;
}
friend int operator % (bign a, int b)
{
for (int i = a._m; i >= 0; i--)
{
if (i == 0) return a._arr[i] % b;
else a._arr[i - 1] += (a._arr[i] % b) * base;
}
}
friend bool operator == (bign a, bign b)
{
if (a._m != b._m) return false;
for (int i = 0; i <= a._m; i++)
if (a._arr[i] != b._arr[i]) return false;
return true;
}
};
int cha_a[110], cha_b[110];
int hm[510], hk[510], rm, rk, rs[510], cs[510];
struct rec
{
LL gcd, crdx, crdy;
rec(void) {}
rec(LL g0, LL cx0, LL cy0) : gcd(g0), crdx(cx0), crdy(cy0) {}
};
// return {d, x, y} : d = gcd(a, b) = ax + by
rec euclid(LL a, LL b)
{
if (b == 0) return rec(a, 1, 0);
else
{
rec ans = euclid(b, a % b);
return rec(ans.gcd, ans.crdy, ans.crdx - (a / b) * ans.crdy);
}
}
// [hhm转移到hhk需要的步数]和[cha以hhk为基准的圈的大小]
pair<int, int> trans(int *cha, int hhm, int hhk)
{
int round = 0, cnt = 0, p = hhm;
while (1)
{
if (p == hhk) break;
else if (cnt && p == hhm) { cnt = -1; break; } // 转了一圈都没有,无解
p = cha[p], ++cnt;
}
if (cnt == -1) return make_pair(-1, 0);
while (1)
{
if (round && p == hhk) break;
p = cha[p], ++round;
} return make_pair(cnt, round); // 圈的大小
}
///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
bign m, k; int d; LL lm, lb, z;
while (1)
{
restart: cin >> d;
if (d == -1) break;
for (int i = 1; i < d; i++) cin >> cha_a[i];
for (int i = 0; i < d; i++) cin >> cha_b[i];
cin >> m >> k;
for (rm = 0; !(m == 0); rm++) // 转为d进制,由低到高位
{
hm[rm] = m % d;
m = m / d;
}
for (rk = 0; !(k == 0); rk++)
{
hk[rk] = k % d;
k = k / d;
}
if (rm != rk) { printf("NO\n"); goto restart; } // 位数不等,无解
for (int i = 0; i < rm - 1; i++) // 除最高位外,用b置换
{
pair<int, int> adp = trans(cha_b, hm[i], hk[i]);
if (adp.first == -1) { printf("NO\n"); goto restart; }
else cs[i] = adp.first, rs[i] = adp.second; // cs第一次能变成的步数,rs圈的大小
}
pair<int, int> adp = trans(cha_a, hm[rm - 1], hk[rm - 1]); // 最高位,用a置换
if (adp.first == -1) { printf("NO\n"); goto restart; }
else cs[rm - 1] = adp.first, rs[rm - 1] = adp.second;
lm = 0, lb = 1;
for (int i = 0; i < rm; i++)
{
rec adp = euclid(lb, rs[i]); // x=c1(mod r1)
if ((lm - cs[i]) % adp.gcd) { printf("NO\n"); goto restart; } // 联立x=c2(mod r2),(c1-c2)=0(mod gcd)才有解
lb = lb / adp.gcd * rs[i]; // lcm
z = adp.crdy * ((lm - cs[i]) / adp.gcd); // 求出k2
lm = z * rs[i] + cs[i]; // 得到方程组的一个最小解
lm = ((lm % lb) + lb) % lb; // 保证最小解大于0
}
printf("%lld\n", lm);
}
#ifndef ONLINE_JUDGE
fclose(stdin);
fclose(stdout);
system("out.txt");
#endif
return 0;
}
///////////////////////////End Sub//////////////////////////////////
| 14183588 | hankcs | 3708 | Accepted | 228K | 0MS | C++ | 4047B | 2015-05-11 17:15:22 |
Reference
![]() 知识共享署名-非商业性使用-相同方式共享:码农场 » POJ 3708 Recurrent Function 题解《挑战程序设计竞赛》
知识共享署名-非商业性使用-相同方式共享:码农场 » POJ 3708 Recurrent Function 题解《挑战程序设计竞赛》
 码农场
码农场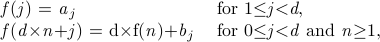
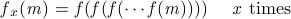
<abbr title=’We