CS224n Assignment 2

3 RNN和语言模型

给定一个词语的序列：

$$\boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}, \dots, \boldsymbol{x}^{(t)}$$

语言模型的任务就是通过建模

$$\begin{align}
P(\boldsymbol{x}^{(t+1)} &= \boldsymbol{v}_{j} \vert \boldsymbol{x}^{(t)}, \dots, \boldsymbol{x}^{(1)})
\end{align}$$

来预测下一个单词$\boldsymbol{x}^{(t+1)}$，其中$\boldsymbol{v}_{j}$是词表中的一个单词。

对RNN来讲，有：

$$\begin{align}
\boldsymbol{e}^{(t)} &= \boldsymbol{x}^{(t)}\boldsymbol{L} \\
%
\boldsymbol{h}^{(t)} &= \text{sigmoid} \left( \boldsymbol{h}^{(t-1)}\boldsymbol{H} + \boldsymbol{e}^{(t)}\boldsymbol{I} + \boldsymbol{b}_{1} \right)\\
%
\hat{\boldsymbol{y}}^{(t)} &= \text{softmax}  \left( \boldsymbol{h}^{(t)}\boldsymbol{U} + \boldsymbol{b}_{2} \right) \\
%
\bar{P}\left( \boldsymbol{x}^{(t+1)} = \boldsymbol{v}_{j} \vert \boldsymbol{x}^{(t)}, \dots, \boldsymbol{x}^{(1)} \right) &= \hat{\boldsymbol{y}}_{j}^{(t)}
\end{align}$$

其中$\boldsymbol{h}^{(0)} = \boldsymbol{h}_{0} \in \mathbb{R}^{D_{k}}$ 是隐藏层的初始状态， $\boldsymbol{L}$ 是lookup-table。参数维度如下：

$$\begin{align}
&\boldsymbol{L} \in \mathbb{R}^{\vert V \vert \times d}
%
&\boldsymbol{H} \in \mathbb{R}^{D_{h} \times D_{h}} \\
%
%
&\boldsymbol{I} \in \mathbb{R}^{d \times D_{h}}
%
&\boldsymbol{b}_{1} \in \mathbb{R}^{D_{h}} \\
%
%
& \boldsymbol{U} \in \mathbb{R}^{D_{h} \times \vert V \vert}
%
& \boldsymbol{b}_{2} \in \mathbb{R}^{\vert V \vert}
\end{align}$$

$d$是嵌入维度，$\vert V \vert$是词表大小，$D_{h}$是隐藏单元数。

输出向量$\hat{\boldsymbol{y}}^{(t)} \in \mathbb{R}^{\vert V \vert}$是词表上的概率分布。模型通过最小化交叉熵损失训练：

$$\begin{align}
J^{(t)}(\theta) = CE(\boldsymbol{y}^{(t)} , \hat{\boldsymbol{y}}^{(t)}) &= - \sum_{j=1}^{\vert V \vert} y_{j}^{(t)} log(\hat{y}_{j}^{(t)})
\end{align}$$

$\boldsymbol{y}^{(t)}$是正确答案的one-hot向量（等于$\boldsymbol{x}^{(t+1)}$）。对单个序列来讲，在所有实例（单词）上取平均。

a 困惑度和交叉熵损失

按惯例，语言模型的效果用困惑度衡量，其定义如下：

$$\begin{align}
\label{eq:perplexity}
PP^{(t)} \left( \boldsymbol{y}^{(t)}, \hat{\boldsymbol{y}}^{(t)} \right) &= \frac{ 1 }{ \bar{P} \left( \boldsymbol{x}_{pred}^{(t+1)} = \boldsymbol{x}^{(t+1)} \vert \boldsymbol{x}^{(t)}, \dots, \boldsymbol{x }^{(1)} \right)} = \frac{ 1 }{ \sum_{j=1}^{\vert V \vert} y_{j}^{(t)} \cdot \hat{y}_{j}^{(t)} }
\end{align}$$

也就是模型分布$\bar{P}$下输出正确答案的概率的倒数。

请从交叉熵推导困惑度。

由于正确答案是one-hot的，所以交叉熵中只有一项不为0：

$$CE(y^{(t)},\hat{y}^{t})=-\log \hat{y}_i^{(t)}=\log \frac{1}{\hat{y}^{t}}$$

$$PP^{(t)}(y^{(t)},\hat{y}^{(t)})=\frac{1}{\hat{y}^{(t)}}$$

$$CE(y^{(t)},\hat{y}^{t})=\log PP^{(t)}(y^{(t)},\hat{y}^{(t)})$$

可见最小化交叉熵的算术平均就相当于最小化困惑度的几何平均。如果模型随机预测，则期望$E[\hat{y}^{(t)}]=\frac{1}{|V|}$，困惑度为其倒数$|V|$，交叉熵为困惑度的对数$\log |V|$。

b 推导梯度

推导损失函数关于下列参数的梯度：

$$\begin{align}
\frac{ \partial J^{(t)} }{ \partial \boldsymbol{b}_{2} }
\quad
\frac{ \partial J^{(t)} }{ \partial \boldsymbol{L}_{x^{(t)}} }
\quad
\frac{ \partial J^{(t)} }{ \partial \boldsymbol{I} } \bigg\rvert_{(t)}
\quad
\frac{ \partial J^{(t)} }{ \partial \boldsymbol{H} } \bigg\rvert_{(t)}
\quad
\frac{\partial J^{(t)}}{\partial \boldsymbol{h}^{(t-1)}}
\end{align}$$

其中， $\boldsymbol{L}_{x^{(t)}}$ 是矩阵 $\boldsymbol{L}$ 对应当前词语 $\boldsymbol{x}^{(t)}$ 的那一行词向量。$\bigg\rvert_{(t)}$代表某个参数在$t$时的取值，而将之前的时刻视作固定值。

把big picture放在眼前

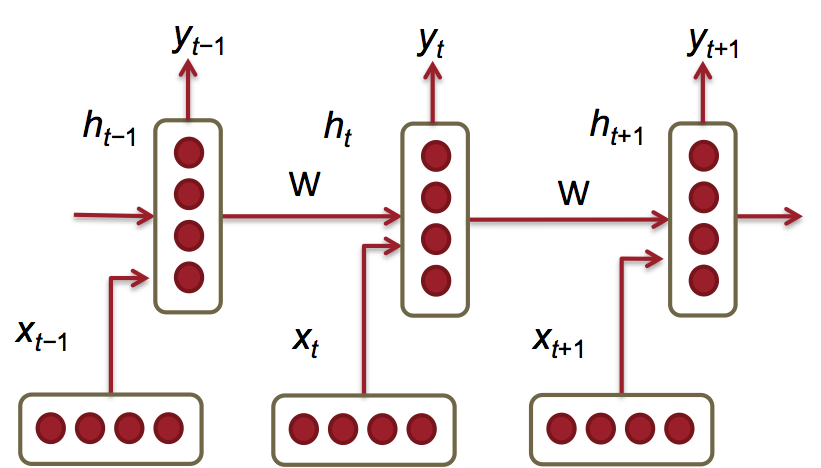
记$\boldsymbol{f}_{1}^{(t)} = \boldsymbol{h}^{(t-1)}\boldsymbol{H} + e^{(t)}\boldsymbol{I} + \boldsymbol{b}_{1}$ 、 $\boldsymbol{f}_{2}^{(t)} = \boldsymbol{h}^{(t)}\boldsymbol{U} + \boldsymbol{b}_{2}$，计算残差：

$$
\begin{align}
\boldsymbol{\delta}_{2}^{(t)} &= \frac{\partial J^{(t)}}{\partial \boldsymbol{f}_{2}^{(t)}} %
    = \hat{\boldsymbol{y}}^{(t)} - \boldsymbol{y}^{(t)} \nonumber \\
%
%
\boldsymbol{\delta}_{1}^{(t)}
&= \frac{\partial J^{(t)}}{\partial \boldsymbol{f}_{1}^{(t)}} \\
&=\frac{\partial \boldsymbol{J}^{(t)}}{\partial \boldsymbol{f}_2^{(t)}} \cdot \frac{\partial \boldsymbol{f}_{2}^{(t)}}{\partial \boldsymbol{h}^{(t)}} \cdot \frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{f}_{1}^{(t)}} \\
    &= \boldsymbol{\delta}_{2}^{(t)} \cdot \frac{\partial \boldsymbol{f}_{2}^{(t)}}{\partial \boldsymbol{h}^{(t)}} \cdot \frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{f}_{1}^{(t)}} \nonumber \\
   &= \boldsymbol{\delta}_{2}^{(t)} \cdot \boldsymbol{U}^{T} \circ \boldsymbol{h}^{(t)} \circ (1 - \boldsymbol{h}^{(t)}) \nonumber
\end{align}
$$

利用这些残差迅速得到结果：

$$\begin{align}
\frac{\partial J^{(t)}}{\partial \boldsymbol{b}_{2}} &= %
\frac{\partial J^{(t)}}{\partial \boldsymbol{f}_{2}^{(t)}} \frac{\partial \boldsymbol{f}_{2}^{(t)}}{\partial \boldsymbol{b}_{2}} \nonumber \\
%
%
  &= \boldsymbol{\delta}_{2}^{(t)} = \hat{\boldsymbol{y}}^{(t)} - \boldsymbol{y}^{(t)} \nonumber
\end{align}$$

$$\begin{align}
\frac{\partial J^{(t)}}{\partial \boldsymbol{L}_{x^{(t)}}} &= %
\frac{\partial J^{(t)}}{\partial \boldsymbol{f}_{1}^{(t)}} \frac{\partial \boldsymbol{f}_{1}^{(t)}}{\partial \boldsymbol{e}^{(t)}} %
\frac{\partial \boldsymbol{e}^{(t)}}{\partial \boldsymbol{L}_{x^{(t)}}} \nonumber \\
%
%
&= \boldsymbol{\delta}_{1}^{(t)} \boldsymbol{I}^{T} \nonumber
\end{align}$$

这里利用到了one-hot向量时$\boldsymbol{e}^{(t)}= \boldsymbol{L}_{x^{(t)}}$。

$$\begin{align}
\frac{\partial J^{(t)}}{\partial \boldsymbol{I}} &= %
\frac{\partial J^{(t)}}{\partial \boldsymbol{f}_{1}^{(t)}} \frac{\partial \boldsymbol{f}_{1}^{(t)}}{\partial \boldsymbol{I}} \nonumber \\
%
%
  &=  (\boldsymbol{e}^{(t)})^{T} \boldsymbol{\delta}_{1}^{(t)}  \nonumber
\end{align}$$

$$\begin{align}
\frac{\partial J^{(t)}}{\partial \boldsymbol{H}} &= %
\frac{\partial J^{(t)}}{\partial \boldsymbol{f}_{1}^{(t)}} \frac{\partial \boldsymbol{f}_{1}^{(t)}}{\partial \boldsymbol{H}} \nonumber \\
%
%
  &= (\boldsymbol{h}^{(t-1)})^{T} \boldsymbol{\delta}_{1}^{(t)} \nonumber
\end{align}$$

$$\begin{align}
\frac{\partial J}{\partial \boldsymbol{h}^{(t-1)}} &= %
\frac{\partial J^{(t)}}{\partial \boldsymbol{f}_{1}^{(t)}} \frac{\partial \boldsymbol{f}_{1}^{(t)}}{\partial \boldsymbol{h}^{(t-1)}} \nonumber \\
%
%
  &=  \boldsymbol{\delta}_{1}^{(t)} \boldsymbol{H}^{T} \nonumber
\end{align}$$

c Backpropagation Through Time

unroll反向传播并计算下列梯度：

$$
\begin{align}
\frac{ \partial J^{(t)} }{ \partial \boldsymbol{L}_{x^{(t-1)}} }
\quad
\frac{ \partial J^{(t)} }{ \partial \boldsymbol{I} } \bigg\rvert_{(t-1)}
\quad
\frac{ \partial J^{(t)} }{ \partial \boldsymbol{H} } \bigg\rvert_{(t-1)}
\end{align}
$$

利用$\boldsymbol{\delta}^{(t-1)} = \frac{\partial J^{(t)}}{\partial \boldsymbol{h}^{(t-1)}}$来简化结果。

真实梯度需要运用反向传播到$t=0$，而实践中经常只运行固定的$\tau \approx 5-10$步。

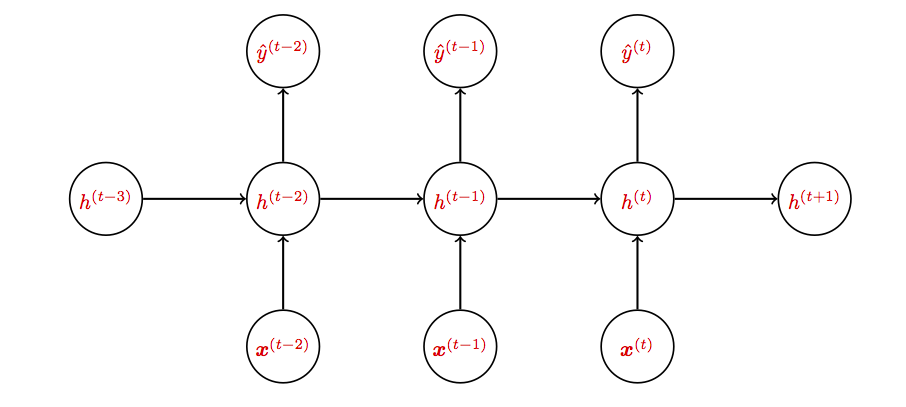
引入新记号$\sigma'(\boldsymbol{f}_{1}^{(t-1)}) = \frac{\partial \boldsymbol{h}^{(t-1)}}{\partial \boldsymbol{f}_{1}^{(t-1)}} = diag\left(\boldsymbol{h}^{(t-1)} \circ (1 - \boldsymbol{h}^{(t-1)}) \right)$

对$\frac{\partial J ^{(t)}}{\partial \boldsymbol{L}_{x^{(t-1)}}}$有

$$\begin{align}
\frac{\partial J ^{(t)}}{\partial \boldsymbol{L}_{x^{(t-1)}}} &= %
\frac{\partial J ^{(t)}}{\partial \boldsymbol{h}^{(t-1)}} %
\frac{\partial \boldsymbol{h}^{(t-1)}}{\partial \boldsymbol{f}_{1}^{(t-1)}} %
\frac{\partial \boldsymbol{f}_{1}^{(t-1)}}{\partial \boldsymbol{L}_{x^{(t-1)}}} \nonumber \\
%
&= \boldsymbol{\delta}^{(t-1)} \sigma'(\boldsymbol{f}_{1}^{(t-1)}) \boldsymbol{I}^{T} \nonumber
\end{align}$$

对$\boldsymbol{I}$有

$$
\begin{align}
\frac{\partial J ^{(t)}}{\partial \boldsymbol{I}} &= %
\frac{\partial J ^{(t)}}{\partial \boldsymbol{h}^{(t-1)}} %
\frac{\partial \boldsymbol{h}^{(t-1)}}{\partial \boldsymbol{v}^{(t-1)}} %
\frac{\partial \boldsymbol{v}^{(t-1)}}{\partial \boldsymbol{I}} \nonumber \\
%
&=  (\boldsymbol{e}^{(t-1)})^{T} \boldsymbol{\delta}_{1}^{(t-1)} \sigma'(\boldsymbol{v}^{(t-1)}) \nonumber
\end{align}
$$

对$H$有

$$
\begin{align}
\frac{\partial J ^{(t)}}{\partial \boldsymbol{H}} &= %
\frac{\partial J ^{(t)}}{\partial \boldsymbol{h}^{(t-1)}} %
\frac{\partial \boldsymbol{h}^{(t-1)}}{\partial \boldsymbol{v}^{(t-1)}} %
\frac{\partial \boldsymbol{v}^{(t-1)}}{\partial \boldsymbol{H}} \nonumber \\
%
&= (\boldsymbol{h}^{(t-2)})^{T} \boldsymbol{\delta}^{(t-1)} \sigma'(\boldsymbol{v}^{(t-1)}) \nonumber
\end{align}
$$

d 计算复杂度

给定$\boldsymbol{h}^{(t-1)}$，前向传播计算$J^{(t)}(\theta)$的复杂度是多少？反向传播$\tau$步呢？

把矩阵运算中涉及到元素数量（维度）估计一下即可。

前向传播：

$$\begin{align}
O\left( (d \times D_{h}) + D_{h}^{2} + (D_{h} \times |V|) \right) \nonumber
\end{align}$$

从左到右3项分别来自输入词向量到隐藏层的权值矩阵、隐藏层到隐藏层的权值矩阵、隐藏层到输出的权值矩阵。

反向传播：

如果对所有单词计算梯度：

$$\begin{align} O\left( \tau \left((d \times D_{h}) + D_{h}^{2} +  D_{h} \times |V| \right)\right) \nonumber
\end{align}$$

这是因为反向传播$\tau$次的路径上，残差来自$\tau$个输出单词。

如果对单个单词计算梯度：

$$\begin{align} O\left( \tau \left((d \times D_{h}) + D_{h}^{2}  \right) +  D_{h} \times |V| \right) \nonumber \end{align}$$

此时反向传播$\tau$次的路径上，来自$\tau$个输出单词的残差中对该单词之外的导数为0。

由于词表远远大于隐藏层节点数$|V|>>D_h$，所以softmax层的$O(D_{h} \times |V|)$是瓶颈。一个解决办法是用NCE代替昂贵的交叉熵损失函数。

References

https://github.com/hankcs/CS224n

https://github.com/rymc9384/DeepNLP_CS224N.git

 知识共享署名-非商业性使用-相同方式共享：码农场 » CS224n Assignment 2