码农场目录
说是机器翻译，其实只涉及最最简单的两个模型：IBM1和2以及启发式改进，用来做文本对齐。代码见文末，包括附加题在内全部达到了预期目标。
文本对齐
文本对齐是这么一个问题，将母语翻译为外语时，给定一个长l的母语句子
和长度m，估计一个长m的外语句子
及后者到前者的对齐方式
的概率
。
无论哪种模型，通用的抽象框架都是一样的。分为两步，先根据e和m得到某个对齐方式a的概率
，然后根据这个a计算对应外语句子f的概率
。
第一步中所谓的对齐方式，其实只是将外语中的每个单词映射到母语的某个单词（多对一），却并不要求母语的每个单词都有对应的外语映射。举个例子：
其中，
。
若
则表示如下对齐方式
英语第一个and就没有对应的法语单词。
甚至可以举个极端的例子：
对应着一个很糟糕的对齐方式：
你也许会很好奇，凭什么多个外语单词能映射到同一个母语单词，反过来却不行呢？对，这的确是个不合实际的约束。加了这个约束后，IBM模型变得简单可实现了，但也带来了失真的问题。接下来的课程Phrase-based_Translation_Models会详细讲这个问题。
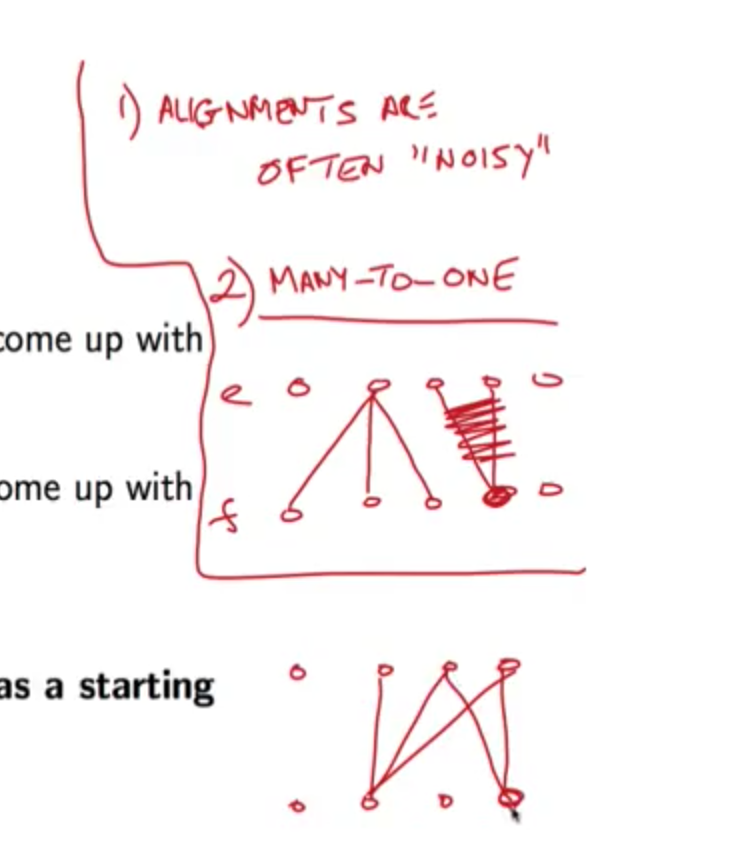
无论如何，要点是第一步不要纠结双方的单词，只得出一个抽象的下标数组。
第二步就要考虑双方单词的这种对应方式存在的概率了。为了表述方便，定义此概率为
，表示已知母语单词e，对应到外语单词f的条件概率。
把两步的概率乘起来，就得到最终的文本对齐概率。
IBM1
第一步，简单地认为所有对齐方式都是等可能的：
=
第二步，简单地认为所有映射关系都是独立的：
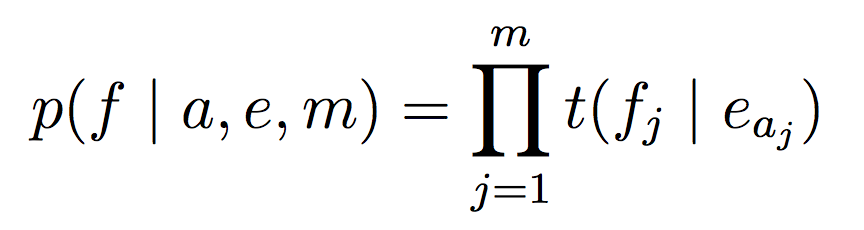
最终得到：
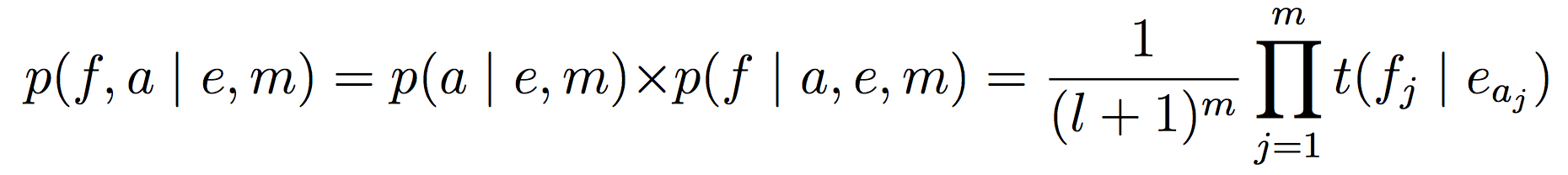
接连做了两个简单粗暴的假设，可以预见这不是个好模型。
IBM2
第一步，对对齐方式的估计，IBM2做了改进：
定义
为给定母语长度l外语长度m，第j个外语单词映射到第i个母语单词的概率，于是有：
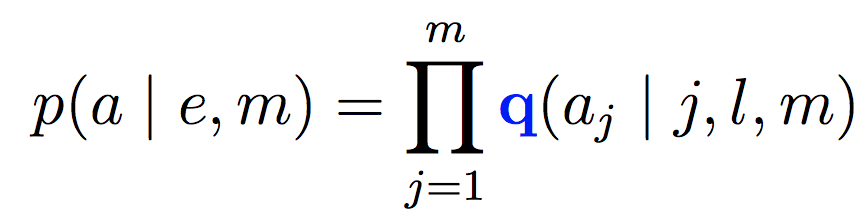
第二步，与IBM1一样：
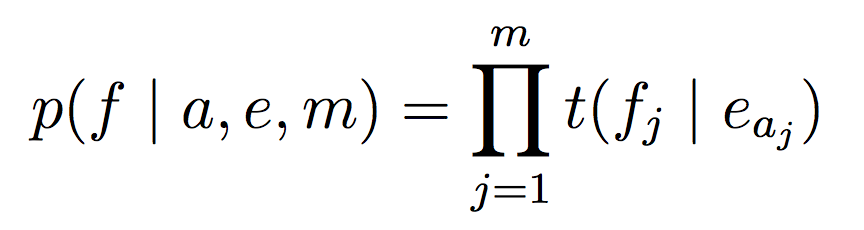
最终得到：
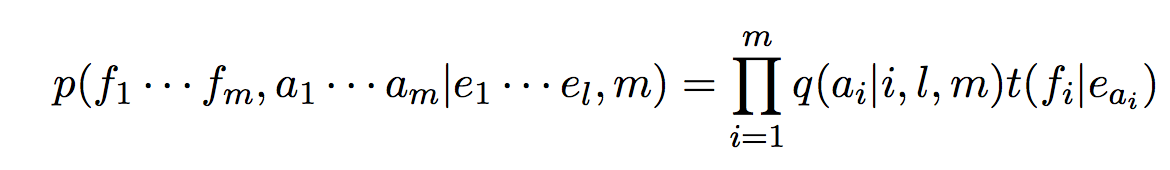
模型大致的框架就是这样了。
参数估计问题
输入训练语料——n个双语句子
，其中
。
输出模型参数——参数
和
，复习一下Micheal Collins在讲义中给出的两者定义：
具体估计时用EM算法，到时候再说。
由于IBM1中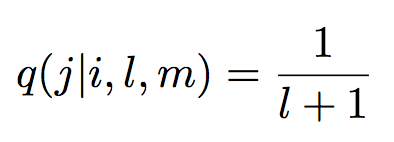
，所以实际上只有一个参数。用Python描述如下：
class IBM1: def __init__(self): self.t = defaultdict(float) # t[(fword, eword)] := t(f|e)
而IBM2就是完整的t和q了：
class IBM2: def __init__(self): self.t = defaultdict(float) # t[(fword, eword)] := t(f|e) self.q = defaultdict(float) # q[(j, i, l, m)] := q(j|i,l,m)
训练数据
训练数据是来自Europarl corpus的英语-西班牙语双语语料：
> head -n 3 corpus.en resumption of the session i declare resumed the session of the european parliament adjourned on ... Although , as you will have seen , the dreaded ’ millennium bug ’ failed ... > head -n 3 corpus.es reanudaci ́on del per ́ıodo de sesiones declaro reanudado el per ́ıodo de sesiones del parlamento europeo ... como todos han podido comprobar , el gran " efecto del a ̃no 2000 " no se ...
评估
如何评估对齐的效果呢？
除了训练数据之外，assignment中还给出了人工标注的对齐数据h3/dev.key：
6 7 3 6 7 4 6 8 5
每行数据的意思是：
SentenceIndex EnglishIndex ForeignIndex
6 7 3代表第6个句子对中，第7个英语词语对应第3个西班牙词语。
• e=Do we want to make it happen?
• f = ¿ Deseamos hacerla realidad ?
整个句子的对齐方式是
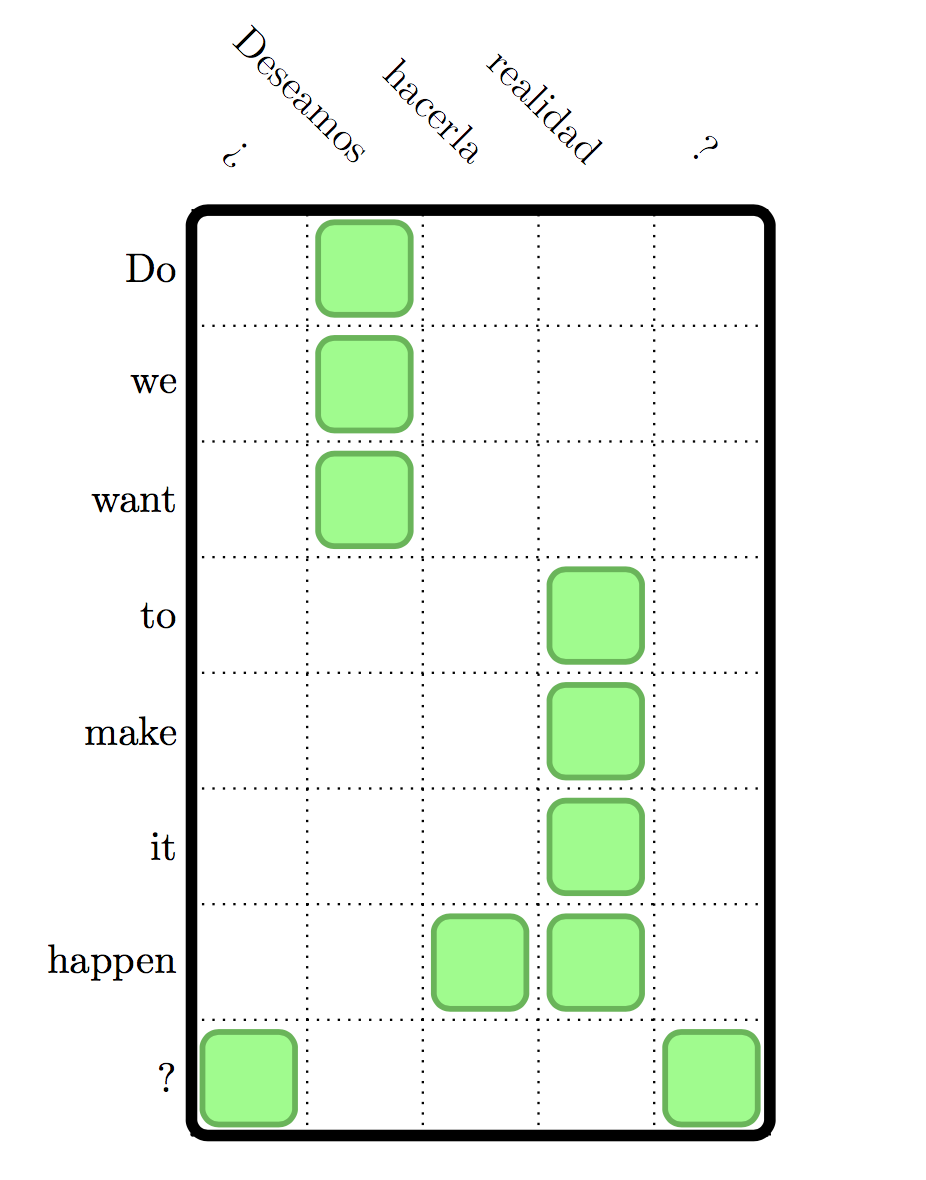
评估脚本h3/eval_alignment.py已经给出，其工作原理很简单，将每行数据读入，做交并集得到各个指标
self.gold += len(gold_set) self.test += len(test_set) self.correct += len(gold_set & test_set)
问题1 IBM Model 1
由于没有标注好的对齐数据，“对齐数据”实际上是个隐变量。此时应该使用含有隐变量的概率模型参数的极大似然估计法，也即EM算法。
定义k为第k个句子，定义
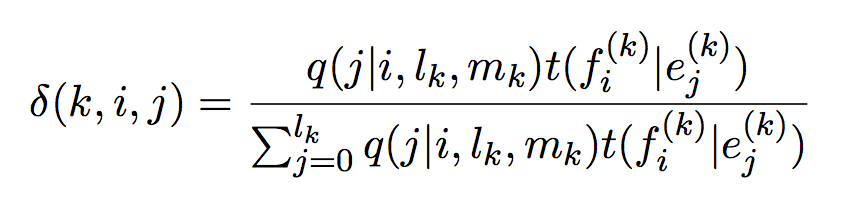
其实是在当前模型参数下
的概率。
在IBM1模型中，简单地认为所有对齐方式都是等可能的
=
所以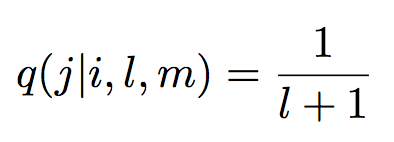，代入上上式有
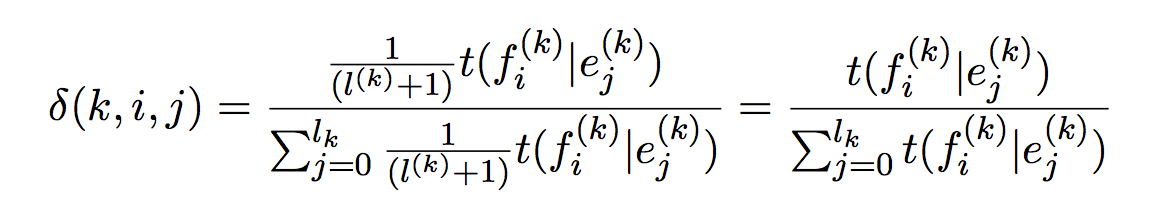
于是得到IBM1的EM算法伪码
初始化的时候可以取随机数，也可以取c(e,f)/c(e)，虽然两者差别并不大。
def initialize(self, corpus): words = defaultdict(float) pairs = defaultdict(float) for e, f in corpus: for eword in e: for fword in f: if (fword, eword) not in pairs: words[eword] += 1.0 pairs[(fword, eword)] = 1.0 for (fword, eword) in pairs: self.t[(fword, eword)] = pairs[(fword, eword)] / words[eword]
其实是的求和，前面说过其实是在当前模型参数下的概率。概率求和得到期望，所以其实是e_j与f_j对齐的期望（可以理解为估计频次）。同理理解
为e_j在母语中的估计词频，同理理解剩下的两个c。
其中每个迭代t和q的更新都用到了最大似然估计：
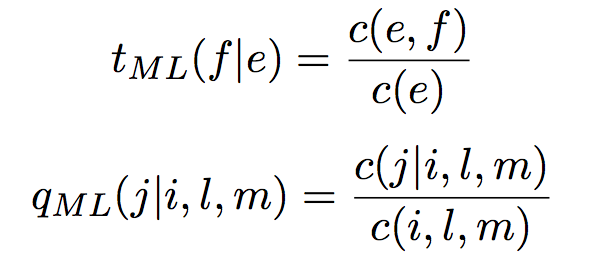
下标ML是maximum-likelihood的缩写。
由于IBM1和IBM2有许多通用的方法，不如写一个wrapper，把model包装起来统一训练，这部分代码
def EM(self, iterations=5): c_fe = defaultdict(int) c_e = defaultdict(int) c_jilm = defaultdict(int) c_ilm = defaultdict(int) t = defaultdict(float) q = defaultdict(float) for s in range(iterations): c_fe.clear() c_e.clear() c_jilm.clear() c_ilm.clear() t.clear() q.clear() for fe, (e, f) in enumerate(self.text): l = len(e) m = len(f) for i, fword in enumerate(f): total, vals = self.model.prob_list(fword, e, i, l, m) for j, eword in enumerate(e): delta = vals[j] / total c_fe[fword, eword] += delta c_e[eword] += delta c_jilm[j, i, l, m] += delta c_ilm[i, l, m] += delta for fe in c_fe: t[fe] = c_fe[fe] / c_e[fe[1]] for j, i, l, m in c_jilm: q[j, i, l, m] = c_jilm[j, i, l, m] / c_ilm[i, l, m] self.model.set_t(t) self.model.set_q(q)
Micheal Collins的讲义（上图伪码）有一处笔误，set了t之后，不需要再set q，保持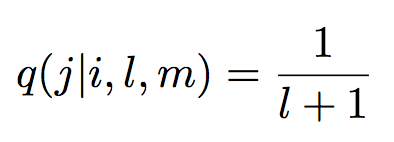即可。
在实现中，IBM1的set_q其实是个空白的方法：
def set_q(self, qvals): pass
IBM1模型测试
既然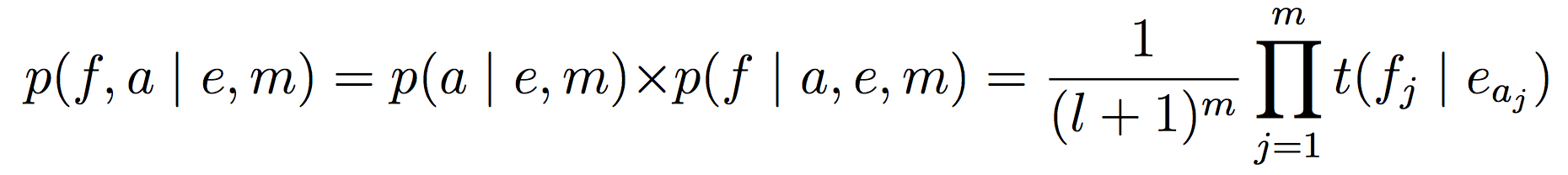，且上下文无联系。那么每一个连乘子项都取最大就行了：
def prob_list(self, fword, e, i, l, m):
a = defaultdict(float)
total = 0.0
for j, eword in enumerate(e):
val = self.t[fword, eword]
total += val
a[j] = val
return total, a
...
for i, fword in enumerate(f):
total, vals = self.model.prob_list(fword, e, i, l, m)
d1 = max(vals, key=(lambda x: vals[x]))
output.write("%s %s %s\n" % (s + 1, i + 1, d1))
调用方法
先执行
model = IBM1()
mt = IBM(model)
mt.read_file("corpus.en", "corpus.es")
mt.EM()
mt.read_dev_file("dev.en", "dev.es", "dev.ibm1.out")
评测
然后跑一跑评测脚本
#!/usr/bin/env bash python eval_alignment.py dev.key dev.out
得到
Type Total Precision Recall F1-Score =============================================================== total 5920 0.413 0.427 0.420
这次assignment的三道题对应的三个预期分值如下：
The expected development F-Scores are 0.420, 0.449, and a basic intersection alignment should give 0.485 for the last part.
问题2 IBM Model 2
理解了IBM1之后，IBM2的训练也没什么复杂的。
比较一下两者，发现唯一的核心不同点在于q的引入，IBM2中的q不再是定值，而是一个可变的参数。为此，引入了另外两个计数器c来统计期望。的概率delta的计算方式也有所不同：
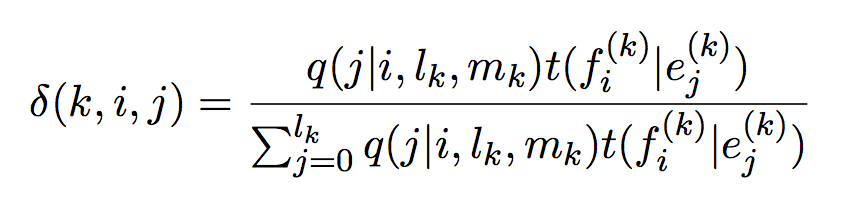
反映在代码上，算法主框架EM不变，但delta计算方法不同。
IBM2模型测试
利用到了q：
def prob_list(self, fword, e, i, l, m):
a = {}
total = 0.0
for j, eword in enumerate(e):
val = self.t[fword, eword] * self.q[j, i, l, m]
total += val
a[j] = val
return total, a
c1和c2的计算与IBM1一致，后面追加了c3和c4。
于是测试的时候也要利用参数q
另外，算法初始化的时候可以直接利用IBM1模型的t作为初值，效果比随机数要好。
调用方法
类似地
model = IBM2()
mt = IBM(model)
mt.read_file("corpus.en", "corpus.es")
mt.EM()
mt.read_dev_file("dev.en", "dev.es", "dev.ibm2.out")
评测
跑跑评估
#!/usr/bin/env bash python eval_alignment.py dev.key dev.ibm2.out
得到
Type Total Precision Recall F1-Score =============================================================== total 5920 0.442 0.456 0.449
效果的确好了一些。
附加问题3：Growing Alignments
上面提到过，答案中允许一个母语单词对齐到多个外语单词（这才是正常的，答案是人工标注的），而IBM模型却不允许。
这道题目探索如何通过IBM模型生成多对多的对齐。事实上，phrase-based translation里面的提取短语就要利用这道题目的思路。
其做法是
1、与问题2相同，估计IBM2的分布
2、将母语视作外语，外语视作母语，送入IBM2估计分布
3、根据和计算各自的最佳对齐
4、计算这两个对齐方式的交集
5、从交集开始，启发式地对齐，启发规则如下：
-
先把交集都采用
-
一次只加一个点
-
只给那些还未对齐的单词添加点
-
优先考虑相邻的点
-
然后考虑其他点
最终效果如下：
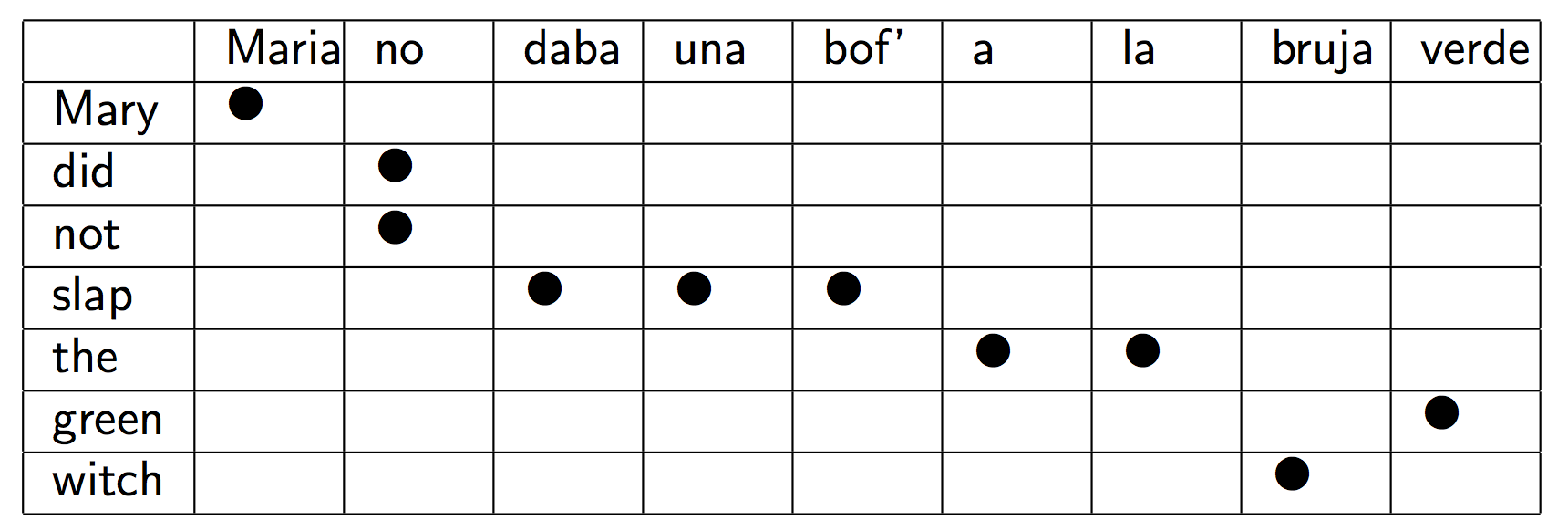
可见最终效果达到了多对多。
实现的时候倒是怪无聊的，无非是一些杂七杂八的规则。
首先直接读入IBM2的输出，免得再去训练啊对齐之类。
def read_alignments(self):
a1 = file("dev.ibm2.out", "r")
a2 = file("dev.ibm2r.out", "r")
for line in a1:
line = line.split(" ")
line[-1] = line[-1].strip()
self.all_f[int(line[0])].append((int(line[1]), int(line[2])))
for line in a2:
line = line.split(" ")
line[-1] = line[-1].strip()
self.all_e[int(line[0])].append((int(line[1]), int(line[2])))
然后取交集和并集，交集全部应用。对并集中的pair，将其视作二维点。对并集的每个点找寻离已应用的pair最近的距离，若最近距离足够小，则认为相邻，也加进去。
既然是规则，必然是丑陋的，什么是足够小？为什么足够小的就是好的？只能说经验证明如此，无法深究。
这些规则如下：
def growing(self): self.uni() self.intersection() self.grow = self.insec.copy() for sent in self.grow: u = self.union[sent] for ef in u: fdone = set([k[1] for k in self.grow[sent]]) edone = set([k[0] for k in self.grow[sent]]) if ef[1] not in fdone or ef[0] not in edone: if self.distance(ef, self.grow[sent]) <= 9: self.grow[sent].append(ef) d1 = [k[0] for k in self.all_e[sent]] d2 = [k[1] for k in self.all_f[sent]] d = math.fabs(max(d1) - max(d2)) + 3 self.grow[sent] = [v for v in self.grow[sent] if math.fabs(v[0] - v[1]) < (d + v[1] / 4)]
距离小于3，然后根据ef最大下标差值过滤一遍，没什么好说的。
调用方法
调用方法如下
model = IBM1()
mt = IBM(model)
mt.read_file("corpus.es", "corpus.en")
mt.EM()
model = IBM2()
mt = IBM(model)
mt.read_file("corpus.es", "corpus.en")
mt.EM()
mt.read_dev_file("dev.es", "dev.en", "dev.ibm2r.out", invert=True)
p = Phrase()
p.read_alignments()
p.growing()
output_dev_file(p.grow, "dev.phase.out")
注意IBM1和2的代码与问题1和2不同，es在前en在后，相当于掉转了母语和外语，得到的是分布。将该分布在dev文件上的输出与问题2合在一起送入Phrase做启发式的growing，得到最终答案。
评测
调用评测脚本
#!/usr/bin/env bash python eval_alignment.py dev.key dev.phase.out
这部分得到
Type Total Precision Recall F1-Score =============================================================== total 5920 0.587 0.457 0.514
超过预期了。
Reference
https://github.com/hankcs/Coursera_NLP_MC
