![]()

求婚:有个贵族向一个贫穷的公主求婚,公主提出条件,需要一种“永生宝石”做嫁妆。这种宝石极其稀有,而且极易损毁,所以开采时需要特别小心。如图:
矿工需要使用一种特殊的金属棒开采,宝石呈圆形,矿床是二维平面,每颗宝石坐标为x,y,半径为r,能够吸附在距离m内的金属棒上。一旦金属棒穿过某个宝石,该宝石就被破坏了。
金属棒非常昂贵,只有一根,作为贵族雇佣的程序员,请你帮他算出能开采到的最大宝石数?
数据格式如下:
N
x1 y1 r1 m1
x2 y2 r2 m2
…
xN yN rN mN
由多个用例组成,输出答案并换行。
3.6与平面和空间打交道的计算几何
极限情况
既然金属棒这么稀有,公主为什么不干脆要金属棒算了。
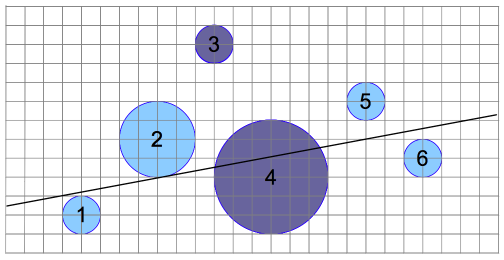
对每个宝石圆,都添加半径扩大m_i的磁力范围圆,将两个圆同时纳入考虑,移动直线的过程中,如果能取到的宝石个数发生变化,那么直线肯定与所有圆中的两个相切,这就是极限情况。所以枚举两个圆的组合确定一条直线,取最大值就行了。
说说很简单,写起来可麻烦了。如果有模板就轻松了,抱着这样的想法我又拿来了osak的模板:
/**
* 对每个宝石圆,都添加半径扩大m_i的磁力范围圆,将两个圆同时纳入考虑
* 移动直线的过程中,如果能取到的宝石个数发生变化,那么直线肯定与所有圆中的两个相切。
* 所以枚举两个圆的组合确定一条直线,取最大值就行了。
*
* 复杂度是O(N^3)。
*/
#include <iostream>
#include <vector>
#include <complex>
#include <cmath>
#include <algorithm>
#include <cassert>
using namespace std;
typedef complex<double> P;
const double PI = acos(-1);
const double EPS = 1e-12;
int cmp(double a, double b)
{
const double diff = a - b;
if (fabs(diff) < EPS)
return 0;
else if (diff < 0)
return -1;
else
return 1;
}
// 向量点乘
inline double dot(const P &a, const P &b)
{
return a.real() * b.real() + a.imag() * b.imag();
}
// 向量叉乘
inline double cross(const P &a, const P &b)
{
return a.real() * b.imag() - b.real() * a.imag();
}
struct line/*{{{*/
{
P a, b;
line()
{}
line(const P &p, const P &q) : a(p), b(q)
{}
// 是否平行
inline bool parallel(const line &ln) const
{
return abs(cross(ln.b - ln.a, b - a)) < EPS; // 平行叉乘得到向量的模是0,也就是sin(theta)=0 <-> theta=0
}
// 是否相交
inline bool intersects(const line &ln) const
{
return !parallel(ln);
}
// 求交点
inline P intersection(const line &ln) const
{
const P x = b - a;
const P y = ln.b - ln.a;
return a + x * (cross(y, ln.a - a)) / cross(y, x);
}
// 点到直线的距离
inline double distance(const P &p) const
{
return abs(cross(p - a, b - a)) / abs(b - a);
}
// 求垂足坐标
inline P perpendicular(const P &p) const
{
const double t = dot(p - a, a - b) / dot(b - a, b - a);
return a + t * (a - b);
}
};
/*}}}*/
struct circle/*{{{*/
{
P o;
double r;
circle()
{}
circle(const P &p, double x) : o(p), r(x)
{}
// 通过点 p 的两条切线
pair<P, P> tangent(const P &p) const
{
const double L = abs(o - p);
const double M = sqrt(L * L - r * r);
const double theta = asin(r / L);
const P v = (o - p) / L;
return make_pair(p + M * (v * polar(1.0, theta)), p + M * (v * polar(1.0, -theta)));
}
// 两个半径相等圆的两条平行外切线
pair<line, line> outer_tangent_parallel(const circle &c) const
{
const P d = o - c.o;
const P v = d * P(0, 1) * r / abs(d);
return make_pair(line(o + v, c.o + v), line(o - v, c.o - v));
}
// 两个圆外切线
pair<line, line> outer_tangent(const circle &c) const
{
if (cmp(r, c.r) == 0)
return outer_tangent_parallel(c);
if (r > c.r)
return c.outer_tangent(*this);
const P d = o - c.o;
const double fact = c.r / r - 1;
const P base = c.o + d + d / fact;
const pair<P, P> t = tangent(base);
return make_pair(line(base, t.first), line(base, t.second));
}
// 内切线
pair<line, line> inner_tangent(const circle &c) const
{
if (r > c.r)
return c.inner_tangent(*this);
const P d = c.o - o;
const double fact = c.r / r + 1;
const P base = o + d / fact;
const pair<P, P> t = tangent(base);
return make_pair(line(base, t.first), line(base, t.second));
}
// 是否相交
inline bool intersects(const circle &c) const
{
return !contains(c) && !c.contains(*this) && cmp(abs(o - c.o), r + c.r) <= 0;
}
// 是否相离
inline bool independent(const circle &c) const
{
return cmp(abs(o - c.o), r + c.r) > 0;
}
// 两个圆的交点
pair<P, P> intersection(const circle &c) const
{
const double d = abs(o - c.o);
const double cos_ = (d * d + r * r - c.r * c.r) / (2 * d);
const double sin_ = sqrt(r * r - cos_ * cos_);
const P e = (c.o - o) / d;
return make_pair(o + e * P(cos_, sin_), o + e * P(cos_, -sin_));
}
// 是否包含圆c
inline bool contains(const circle &c) const
{
return cmp(abs(o - c.o) + c.r, r) < 0;
}
// 是否相交
inline bool intersects(const line &ln) const
{
return cmp(abs(ln.distance(o)), r) <= 0;
}
// 圆心到直线的距离
inline double distance(const line &ln) const
{
return abs(ln.distance(o));
}
// 圆与直线的交点
pair<P, P> intersection(const line &ln) const
{
const P h = ln.perpendicular(o);
const double d = abs(h - o);
P ab = ln.b - ln.a;
ab /= abs(ab);
const double l = sqrt(r * r - d * d);
return make_pair(h + l * ab, h - l * ab);
}
};
/*}}}*/
void enum_event(const circle &c1, const circle &c2, vector<line> &lines)
{
if (c1.independent(c2)) // c1 c2相离
{
auto outer = c1.outer_tangent(c2);
lines.push_back(outer.first);
lines.push_back(outer.second);
auto inner = c1.inner_tangent(c2);
lines.push_back(inner.first);
lines.push_back(inner.second);
}
else if (c1.intersects(c2)) // 相交
{
auto outer = c1.outer_tangent(c2);
lines.push_back(outer.first);
lines.push_back(outer.second);
auto inter = c1.intersection(c2);
lines.push_back(line(inter.first, inter.second)); // 此时内切线不存在,使用交点形成的线代替
}
}
bool solve()
{
int N;
cin >> N;
if (!N)
return false;
vector<pair<circle, circle>> jewels;
vector<line> lines;
for (int i = 0; i < N; ++i)
{
double x, y, r, m;
cin >> x >> y >> r >> m;
const P center(x, y);
pair<circle, circle> jewel = make_pair(circle(center, r), circle(center, r + m));
for (const auto &other : jewels)
{
enum_event(jewel.first, other.first, lines);
enum_event(jewel.first, other.second, lines);
enum_event(jewel.second, other.first, lines);
enum_event(jewel.second, other.second, lines);
}
jewels.push_back(jewel);
}
int ans = 1;
for (auto &l : lines)
{
int cnt = count_if(jewels.begin(), jewels.end(), [&](const pair<circle, circle> &j) { // [&] 按引用捕获在lambda表达式所在函数的函数体中提及的全部自动储存持续性变量
return cmp(j.first.r, j.first.distance(l)) <= 0 && cmp(j.second.r, j.second.distance(l)) >= 0; // 在磁力圆范围内且不在本体范围内
});
ans = max(ans, cnt);
}
cout << ans << endl;
return true;
}
///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
cin.tie(0);
ios::sync_with_stdio(0);
while (solve());
#ifndef ONLINE_JUDGE
fclose(stdin);
fclose(stdout);
system("out.txt");
#endif
return 0;
}
///////////////////////////End Sub//////////////////////////////////
上面C++11估计会造成眩晕效果,关于lambda表达式请参考这里。
提交结果是:
Judge Not Available的原因据说是后台数据维护。
不过就算AC了公主也不会嫁给你这个穷码农的!
![]() 知识共享署名-非商业性使用-相同方式共享:码农场 » AOJ 2201 Immortal Jewels 题解 《挑战程序设计竞赛》
知识共享署名-非商业性使用-相同方式共享:码农场 » AOJ 2201 Immortal Jewels 题解 《挑战程序设计竞赛》
 码农场
码农场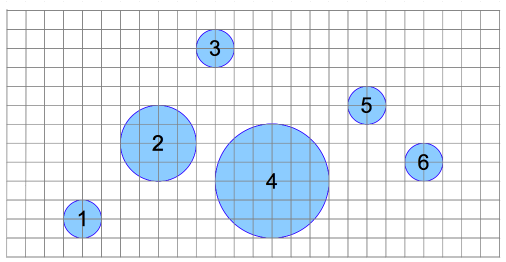
55555555,身为码农,无地自容