POJ 1418 Viva Confetti 题解 《挑战程序设计竞赛》

POJ 1418 Viva Confetti

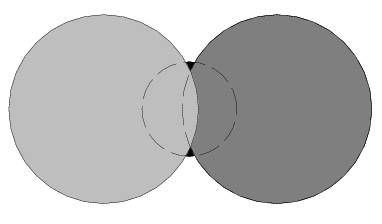
礼花：Confetti 是一些大小不一的彩色圆形纸片，人们在派对上、过节时便抛洒它们以示庆祝。落在地上的Confetti会堆叠起来，以至于一部分会被盖住而看不见。给定Confetti的尺寸和位置以及它们的叠放次序，你能计算出有多少Confetti是可以看见的吗？

3.6与平面和空间打交道的计算几何 

极限情况 

非常需要想象力，某个圆上方的所有圆构成了一个遮罩：

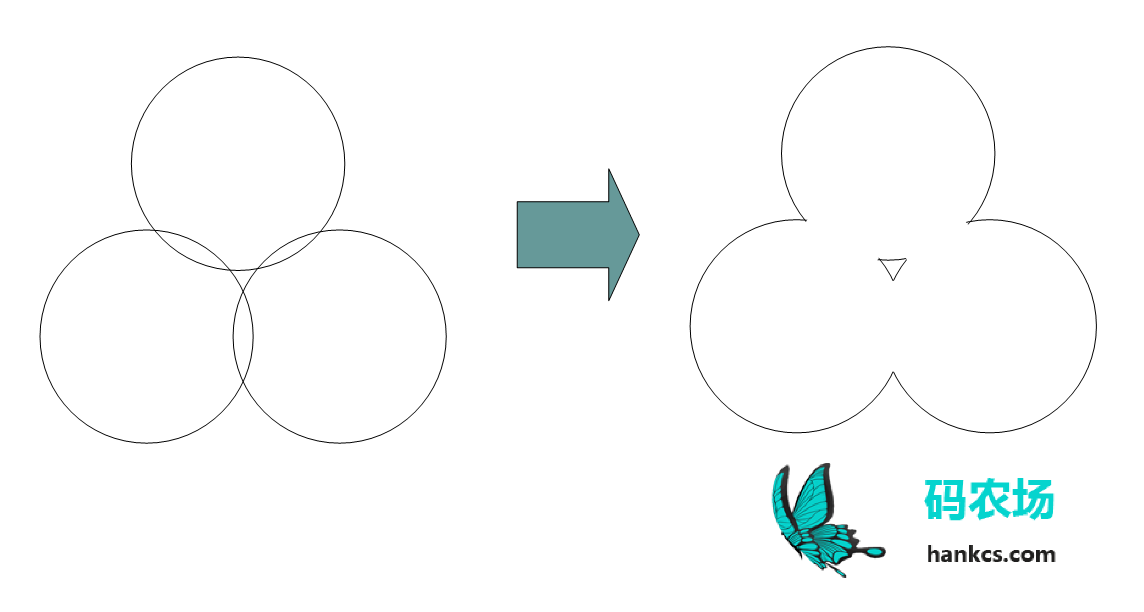
与遮罩的边界相交的圆是可见的，从上图中间的缝看到的也可见，当然也存在完全不被遮罩覆盖的特例：

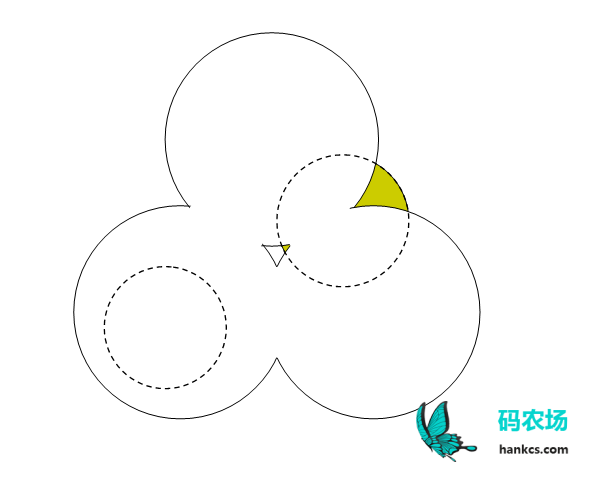
如果直接考虑下面这个圆可不可见，想想还是挺麻烦的。但是遮罩肯定可见，于是转换思路，给定一个底层圆，判断它的上层圆哪些可见（不要求确定每一个上层圆）？

对某一个圆，计算该圆与其他所有圆的交点，以极角表示。这里未必非要“上层圆”的交点，下层也无妨，因为待会儿枚举中点的时候是从上往下取第一个的，这样实际上还是取了上层遮罩。多枚举没关系，只要不少枚举就行。

对于所有例子（包含特例），都认为0和2π是两个交点（实际上是同一个点，对应一段长度为0的弧）。排序后相邻两个交点的中点取稍微靠内与靠外的两个点，这两个点从上到下落入的第一个圆（遮罩中的某个圆）一定是可见的。此时相邻两个交点构成的弧不是上图的橙色高亮部分，而是被分割的虚线部分。

至于极角的计算，依然一图流：

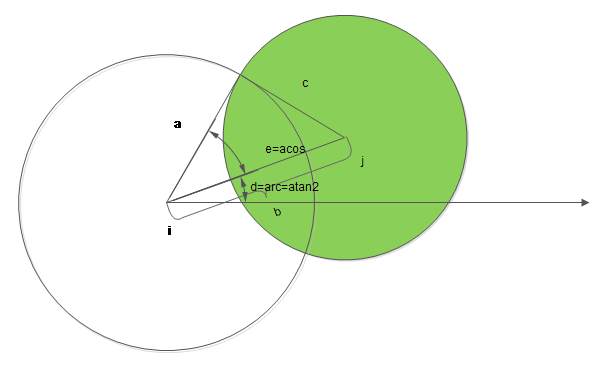
#include <iostream>
#include <algorithm>
#include <vector>
#include <complex>
#include <cmath>

using namespace std;

typedef complex<double> P;
#define M_PI 3.14159265358979323846
#define EPS 4E-13

//************************************
// Returns:   将极角转为[0, 2pi)之间
// Parameter: double r
//************************************
double normalize(double r)
{
	while (r < 0.0)
		r += 2 * M_PI;
	while (r >= 2 * M_PI)
		r -= 2 * M_PI;
	return r;
}

//************************************
// Returns:   从上到下点落入的第一个圆的下标，
// 点没被覆盖则返回-1
// Parameter: vector<P> & points
// Parameter: vector<double> & rs
//************************************
int hit_test(P p, vector<P> &points, vector<double> &rs)
{
	for (int i = rs.size() - 1; i >= 0; --i)
	if (abs(points[i] - p) < rs[i])
		return i;
	return -1;
}


///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
#endif
	int n;
	while (scanf("%d", &n), n)
	{
		vector<P> points;
		vector<double> rs;
		for (int i = 0; i < n; ++i)
		{
			double x, y, r;
			scanf("%lf%lf%lf", &x, &y, &r);
			points.push_back(P(x, y));
			rs.push_back(r);
		}
		vector<bool> visible(n, false);
		for (int i = 0; i < n; ++i) // 从最下面一个开始处理
		{
			vector<double> rads;	// 与其他圆相交的弧的极角
			rads.push_back(0.0);
			rads.push_back(2.0 * M_PI);
			for (int j = 0; j < n; j++)
			{
				double a = rs[i];
				double b = abs(points[j] - points[i]);
				double c = rs[j];
				if (a + b < c || a + c < b || b + c < a)	// 构不成三角形，两圆不相交
					continue;
				double d = arg(points[j] - points[i]);
				double e = acos((a * a + b * b - c * c) / (2 * a * b));
				rads.push_back(normalize(d + e));	// 用极角表示的圆弧的两个端点
				rads.push_back(normalize(d - e));
			}
			sort(rads.begin(), rads.end());
			for (int j = 0; j < rads.size() - 1; j++)
			{
				double rad = (rads[j + 1] + rads[j]) / 2.0;	// 中点与圆心构成的极角
				for (int k = -1; k <= 1; k += 2)			// 中点在圆弧内外的两个点
				{
					int t = hit_test(P(points[i].real() + (rs[i] + EPS * k) * cos(rad), points[i].imag() + (rs[i] + EPS * k) * sin(rad)), points, rs);
					if (t != -1)
						visible[t] = true;
				}
			}
		}
		printf("%d\n", count(visible.begin(), visible.end(), true));
	}
#ifndef ONLINE_JUDGE
	fclose(stdin);
	fclose(stdout);
	system("out.txt");
#endif
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

Reference

1418 viva confetti.ppt

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 1418 Viva Confetti 题解 《挑战程序设计竞赛》