POJ 1981 Circle and Points 题解 《挑战程序设计竞赛》

POJ 1981 Circle and Points

套圈：平面上有N个点，用单位圆去套，最多能套几个？

3.6与平面和空间打交道的计算几何 

极限情况 

所谓极限情况就是单位圆上有两个点，稍微动一下就会损失一个点，覆盖点最多的圆一定有一个是这种圆（当然当N=1的时候是个例外）。朴素想法是先固定两个点，然后枚举其他的点是否在这两个点决定的两个圆内，朴素得掉渣我就不写了。

更快的算法是，先只固定一个点i，该点的单位圆与其他点j的单位圆相交，形成i圆上的一段弧，该弧被j圆覆盖。最终圆如果在该弧上，则一定能覆盖j点。那么问题归结于找出i圆上被覆盖次数最多的一段弧。

至于弧的表示，用两个极角表示，分别为起始和终止，类似于一个区间。枚举完其他点之后，得到N-1个区间。将其排序后，从前往后扫描，碰到起始计数+1，碰到终止计数-1，同时更新答案。

至于极角的求解，三角函数我全忘光了……查了查维基才记起来，如图：

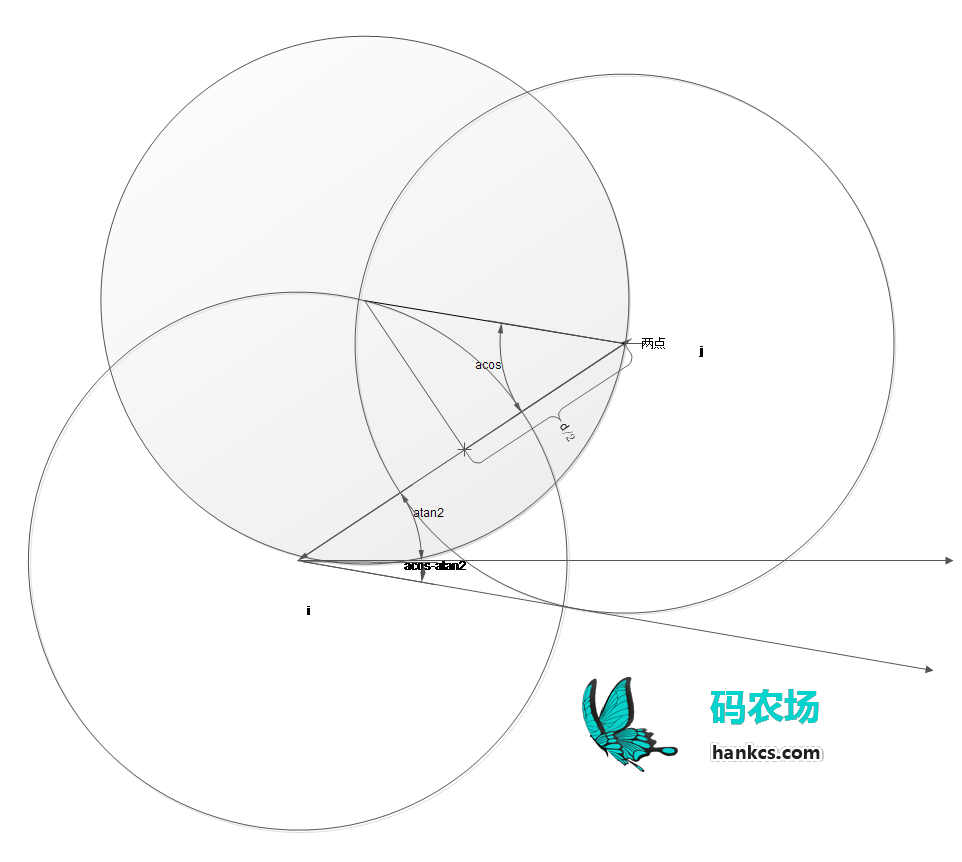
其中，acos的定义如下：

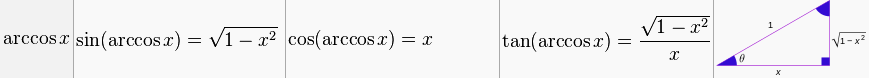
atan2的定义如下：

那么就可以愉快地写代码了：

#include<cstdio>
#include<cmath>
#include<algorithm>

using namespace std;

#define MAX_N 300 + 16

typedef double p_type;

struct Point
{
	p_type x, y;

	Point(){}

	Point(p_type x, p_type y) : x(x), y(y){}
} ps[MAX_N];

struct PolarAngle
{
	p_type angle;
	bool flag;	// 起点或终点

	const bool operator<(const PolarAngle &other)
	{
		return angle < other.angle;
	}
} as[MAX_N];

inline p_type distance_of(const Point &P, const Point &Q)
{
	return sqrt((P.x - Q.x) * (P.x - Q.x) + (P.y - Q.y) * (P.y - Q.y));
}

inline int solve(const int& n, const p_type& r)
{
	int result = 1;
	for (int i = 0; i < n; ++i)
	{
		int m = 0;
		double d;
		for (int j = 0; j < n; ++j)
		{
			if (i != j && (d = distance_of(ps[i], ps[j])) <= 2)
			{
				double phi = acos(d / 2);
				double theta = atan2(ps[j].y - ps[i].y, ps[j].x - ps[i].x);
				as[m].angle = theta - phi, as[m++].flag = 1;
				as[m].angle = theta + phi, as[m++].flag = 0;
			}
		}
		sort(as, as + m);
		for (int sum = 1, j = 0; j < m; ++j)
		{
			if (as[j].flag)
				++sum;
			else
				--sum;
			result = max(result, sum);
		}
	}
	return result;
}

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
#endif
	int N;
	while (scanf("%d", &N), N)
	{
		for (int i = 0; i < N; ++i)
		{
			scanf("%lf%lf", &ps[i].x, &ps[i].y);
		}
		printf("%d\n", solve(N, 1.0));
	}
#ifndef ONLINE_JUDGE
	fclose(stdin);
	fclose(stdout);
	system("out.txt");
#endif
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 1981 Circle and Points 题解 《挑战程序设计竞赛》