AOJ 2230 How to Create a Good Game 题解《挑战程序设计竞赛》-码农场

3.5借助水流解决问题的网络流
最小费用流

挑战程序设计竞赛

游戏设计：国际游戏公司ICPC (International Company for Playing and Competing)要加工一个游戏，该游戏的关卡是一个有向无环图，每两个关卡间都有若干任务。在通关所需最多任务不变的情况下，还能最多增添多少任务？

3.5借助水流解决问题的网络流

最小费用流

不愧是ICPC，业务广，难度大。如果将原DAG权值取反，然后从最后一关连一条正权边到第一关，权值是最短路（负权值最短路=传统意义上的最长路）的长度的话，那么那些正圈中的负权边就是应该增加权值的边，具体应该加多少，就是正圈的权值。

再看怎么用网络流计算这些正圈权值，新建源点汇点，对于所有顶点，如果入度>出度，从源点连一条边到它，否则，从它连一条边到汇点，容量都是是度数差。比如对于：

顶点编号+1，建立网络流：

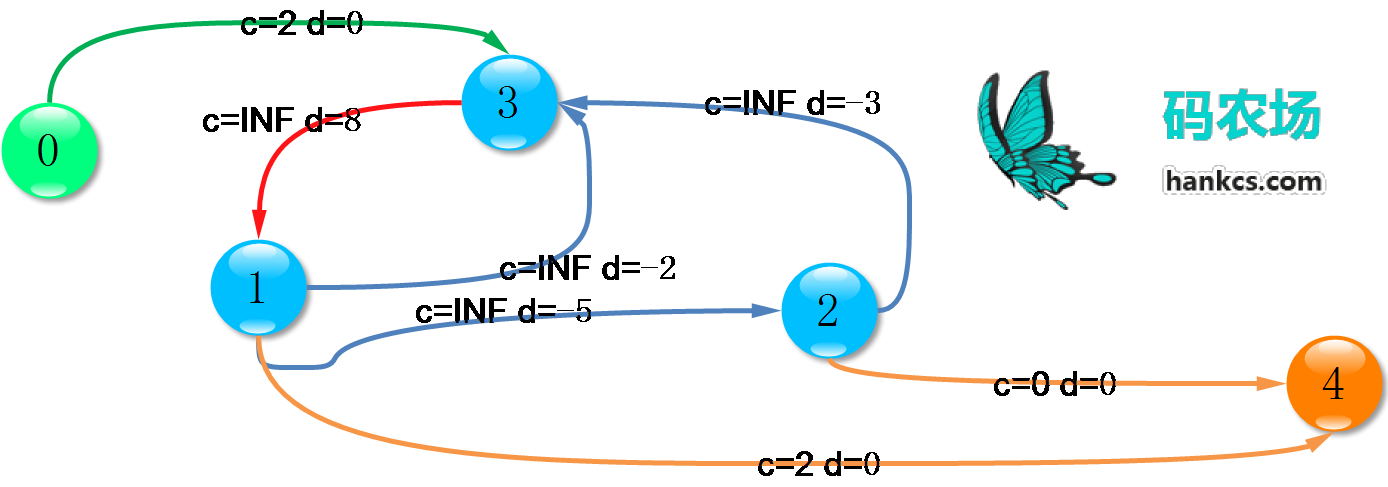
How to Create a Good Game.png

在上面跑F=源点cap总和的最小费用流，得到的就是每个圈的正边（红色）权值之和，在将其加上所有圈的负边（蓝色）之和，就是所有正圈的权值之和，也就是最终答案。给出我的代码：

#include <cstdio>
#include <vector>
#include <algorithm>
#include <queue>
#include <functional>
#include <cstring>

using namespace std;

#define MAX_V 100 + 2
int indegree[MAX_V], outdegree[MAX_V];
int n, m, s, t;

#define INF 0x3f3f3f3f
///////////////////////////////最小费用流开始///////////////////////////////////////////
typedef pair<int, int> P;  // first保存最短距离，second保存顶点编号
//用于表示边的结构体
struct edge
{
	int to;        // 终点
	int cap;   // 容量
	int cost;  // 费用
	int rev;   // 反向边
	edge(int to, int cap, int cost, int rev) :to(to), cap(cap), cost(cost), rev(rev){}
};
int V;         // 顶点数
vector<edge> G[MAX_V];   // 图的邻接表
int h[MAX_V];  // 顶点的势
int dist[MAX_V];// 最短距离
int prevv[MAX_V];  // 最短路中的前驱节点
int preve[MAX_V];  // 最短路中的前驱节点对应的边

// 向图中增加一条从from到to的容量为cap费用为cost的边
void add_edge(int from, int to, int cap, int cost)
{
	G[from].push_back(edge(to, cap, cost, G[to].size()));
	G[to].push_back(edge(from, 0, -cost, G[from].size() - 1));
}

// 求解从s到t流量为f的最小费用流，如果没有流量为f的流，则返回-1
int min_cost_flow(int s, int t, int f)
{
	int res = 0;
	memset(h, 0, sizeof(h));
	while (f > 0)
	{
		// 使用Dijkstra算法更新h
		priority_queue<P, vector<P>, greater<P> > que;
		memset(dist, INF, sizeof(dist));
		dist[s] = 0;
		que.push(P(0, s));
		while (!que.empty())
		{
			P p = que.top(); que.pop();
			int v = p.second;
			if (dist[v] < p.first) continue;
			for (int i = 0; i < G[v].size(); ++i)
			{
				edge &e = G[v][i];
				if (e.cap > 0 && dist[e.to] > dist[v] + e.cost + h[v] - h[e.to])
				{
					dist[e.to] = dist[v] + e.cost + h[v] - h[e.to];
					prevv[e.to] = v;
					preve[e.to] = i;
					que.push(P(dist[e.to], e.to));
				}
			}
		}
		if (dist[t] == INF)
		{
			// 不能再增广
			return -1;
		}
		for (int v = 0; v < V; ++v)
		{
			h[v] += dist[v];
		}

		// 沿s到t的最短路尽量增广
		int d = f;
		for (int v = t; v != s; v = prevv[v])
		{
			d = min(d, G[prevv[v]][preve[v]].cap);
		}
		f -= d;
		res += d * h[t];
		for (int v = t; v != s; v = prevv[v])
		{
			edge &e = G[prevv[v]][preve[v]];
			e.cap -= d;
			G[v][e.rev].cap += d;
		}
	}
	return res;
}
///////////////////////////////最小费用流结束///////////////////////////////////////////

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
	scanf("%d%d", &n, &m);
	V = n + 2;
	t = V - 1;

	int total = 0;
	for (int i = 1; i <= m; i++)
	{
		int x, y, z;
		scanf("%d%d%d", &x, &y, &z);
		x++, y++;
		add_edge(x, y, INF, -z);
		outdegree[x]++, indegree[y]++;
		total += z;
	}

	int max_f = 0;
	for (int i = 1; i <= n; i++)
	{
		if (indegree[i] > outdegree[i])
		{
			add_edge(s, i, indegree[i] - outdegree[i], 0);
			max_f += indegree[i] - outdegree[i];
		}
		else
		{
			add_edge(i, t, outdegree[i] - indegree[i], 0);
		}
	}

	min_cost_flow(1, n, 1);
	add_edge(n, 1, INF, -dist[n]);
	int ans = min_cost_flow(s, t, max_f);
	printf("%d\n", ans - total);
	return 0;
}
///////////////////////////End Sub//////////////////////////////////