POJ 1466 Girls and Boys 题解 《挑战程序设计竞赛》

POJ 1466 Girls and Boys

FFF团：

有V个学生，每行数据x: (n) y z … 表示学生x与另n个人：y和z……有一腿（贵圈真乱）。不知为何，你手中突然多出了火把和汽油。在放火温暖全世界之前，你想豁免尽可能多的单身狗，求最大单身狗集合大小。

3.5借助水流解决问题的网络流 

二分图匹配

赤裸裸的最大独立集，基本概念：

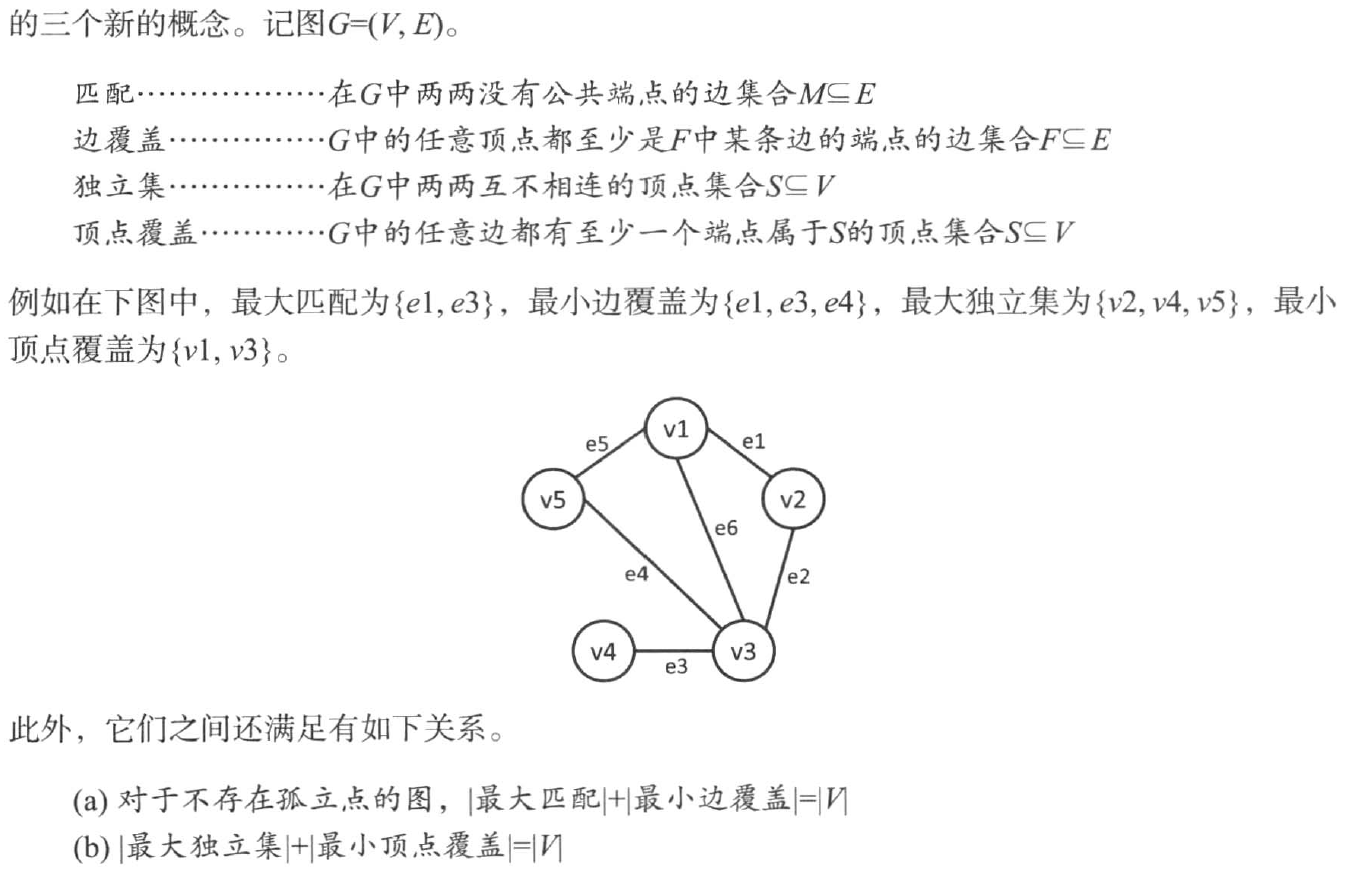
由|最大独立集|+|最小顶点覆盖|=|V| 和 |最大匹配|=|最小顶点覆盖| 得到 |最大独立集|=|V|-|最大匹配|。

#include <iostream>
#include <vector>
using namespace std;

////////////////////////最大流开始//////////////////////////////////////
#define MAX_V 500 + 16
int V;                 // 顶点数
vector<int> G[MAX_V];    // 图的邻接表
int match[MAX_V];      // 所匹配的顶点
bool used[MAX_V];      // DFS中用到的访问标记

// 向图中增加一条连接u和v的边
void add_edge(int u, int v)
{
	G[u].push_back(v);
	G[v].push_back(u);
}

// 通过DFS寻找增广路
bool dfs(int v)
{
	used[v] = true;
	for (vector<int>::iterator it = G[v].begin(); it != G[v].end(); ++it)
	{
		int u = *it, w = match[u];
		if (w < 0 || !used[w] && dfs(w))
		{
			match[v] = u;
			match[u] = v;
			return true;
		}
	}

	return false;
}

// 求解二分图的最大匹配
int bipartite_matching()
{
	int res = 0;
	memset(match, -1, sizeof(match));
	for (int v = 0; v < V; ++v)
	{
		if (match[v] < 0)
		{
			memset(used, 0, sizeof(used));
			if (dfs(v))
			{
				++res;
			}
		}
	}

	return res;
}

void clear()
{
	for (int i = 0; i < V; ++i)
	{
		G[i].clear();
	}
}

///////////////////////////////最大流结束/////////////////////////////////////

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
#endif
	while (scanf("%d", &V) != EOF)
	{
		clear();
		for (int i = 0; i < V; ++i)
		{
			int v, m, u;
			scanf("%d: (%d)", &v, &m);
			for (int j = 0; j < m; ++j)
			{
				scanf("%d", &u);
				G[v].push_back(u);
			}
		}
		printf("%d\n", V - bipartite_matching());
	}
#ifndef ONLINE_JUDGE
	fclose(stdin);
	fclose(stdout);
	system("out.txt");
#endif
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 1466 Girls and Boys 题解 《挑战程序设计竞赛》