POJ 1486 Sorting Slides 题解 《挑战程序设计竞赛》

POJ 1486 Sorting Slides

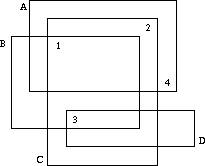
故纸堆：桌上有n张幻灯片杂乱地叠在一起，给出每张幻灯片的边界和页码坐标，求在不翻动的情况下哪些页码可以确定？

3.5借助水流解决问题的网络流 

二分图匹配

如果页码u坐标落在幻灯片v内，则建立一条边(u,v)，在完全图上跑二分图匹配必然完美，如果删掉某一条边后变不完美了，说明这条边的对应关系是确定的。

#include <iostream>
#include <vector>
#include <queue>

using namespace std;
#define MAX_N 26
////////////////////////最大流开始//////////////////////////////////////
#define MAX_V MAX_N * 2
int V;                 // 顶点数
vector<int> G[MAX_V];    // 图的邻接表
int match[MAX_V];      // 所匹配的顶点
bool used[MAX_V];      // DFS中用到的访问标记

// 向图中增加一条连接u和v的边
void add_edge(int u, int v)
{
	G[u].push_back(v);
	G[v].push_back(u);
}

// 通过DFS寻找增广路
bool dfs(int v)
{
	used[v] = true;
	for (vector<int>::iterator it = G[v].begin(); it != G[v].end(); ++it)
	{
		int u = *it, w = match[u];
		if (w < 0 || !used[w] && dfs(w))
		{
			match[v] = u;
			match[u] = v;
			return true;
		}
	}

	return false;
}

// 求解二分图的最大匹配
int bipartite_matching()
{
	int res = 0;
	memset(match, -1, sizeof(match));
	for (int v = 0; v < V; ++v)
	{
		if (match[v] < 0)
		{
			memset(used, 0, sizeof(used));
			if (dfs(v))
			{
				++res;
			}
		}
	}

	return res;
}

void clear()
{
	for (int i = 0; i < V; ++i)
	{
		G[i].clear();
	}
}

///////////////////////////////最大流结束/////////////////////////////////////
struct Point
{
	int x, y;
}P[MAX_N];
struct Slide
{
	int xmin, xmax, ymin, ymax;

	bool contain(const Point& p)
	{
		return xmin < p.x && p.x < xmax && ymin < p.y && p.y < ymax;
	}
} S[MAX_N];
///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
#endif
	int n, id = 0;
	while (scanf("%d", &n) && n)
	{
		V = 2 * n;

		for (int i = 0; i < n; ++i)
		{
			scanf("%d%d%d%d", &S[i].xmin, &S[i].xmax, &S[i].ymin, &S[i].ymax);
		}

		for (int i = 0; i < n; ++i)
		{
			scanf("%d%d", &P[i].x, &P[i].y);
		}

		int slide_id[MAX_N];
		memset(slide_id, -1, sizeof(slide_id));
		
		for (int i = 0; i < n; ++i)
		{
			int match_count = 0;
			for (int k = 0; k < n; ++k)
			{
				if (S[i].contain(P[k]))			// 删掉掉i->k这个边
				{
					clear();
					for (int j = 0; j < n; ++j)
					{
						if (i != j)
						{
							for (int l = 0; l < n; ++l)
							{
								if (k != l)
								{
									if (S[j].contain(P[l]))
									{
										add_edge(j, n + l);
									}
								}
							}
						}
					}
					if (bipartite_matching() == n - 1)	// 发现匹配变得不完美了，说明它是确定的
					{
						++match_count;
						slide_id[i] = k;
					}
				}
			}
			if (match_count != 1)
			{
				slide_id[i] = -1;
			}
		}
		
		printf("Heap %d\n", ++id);
		bool has_one = false;
		for (int i = 0; i < n; ++i)
		{
			if (slide_id[i] != -1)
			{
				printf("%s(%c,%d)", (has_one ? " " : ""), i + 'A', slide_id[i] + 1);
				has_one = true;
			}
		}
		if (has_one)
		{
			puts("");
		}
		else
		{
			puts("none");
		}
		puts("");
	}
#ifndef ONLINE_JUDGE
	fclose(stdin);
	fclose(stdout);
	system("out.txt");
#endif
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 1486 Sorting Slides 题解 《挑战程序设计竞赛》