POJ 2082 Terrible Sets​ 题解《挑战程序设计竞赛》

POJ 2082 Terrible Sets 

最大矩形：柱状图是由一些宽度相等的长方形下端对齐后横向排列得到的图形。现在有由n个宽度分别为w_i，高度分别为h_i的长方形从左到右依次排列组成的柱状图。问里面包含的长方形的最大面积是多少。

4.4常用技巧精选（二） 

栈 

讨厌中国人出的英文题，明明可以用形象的语言去描述，却非要用一堆排版粗劣的公式，还自以为很幽默。

画个图一目了然：

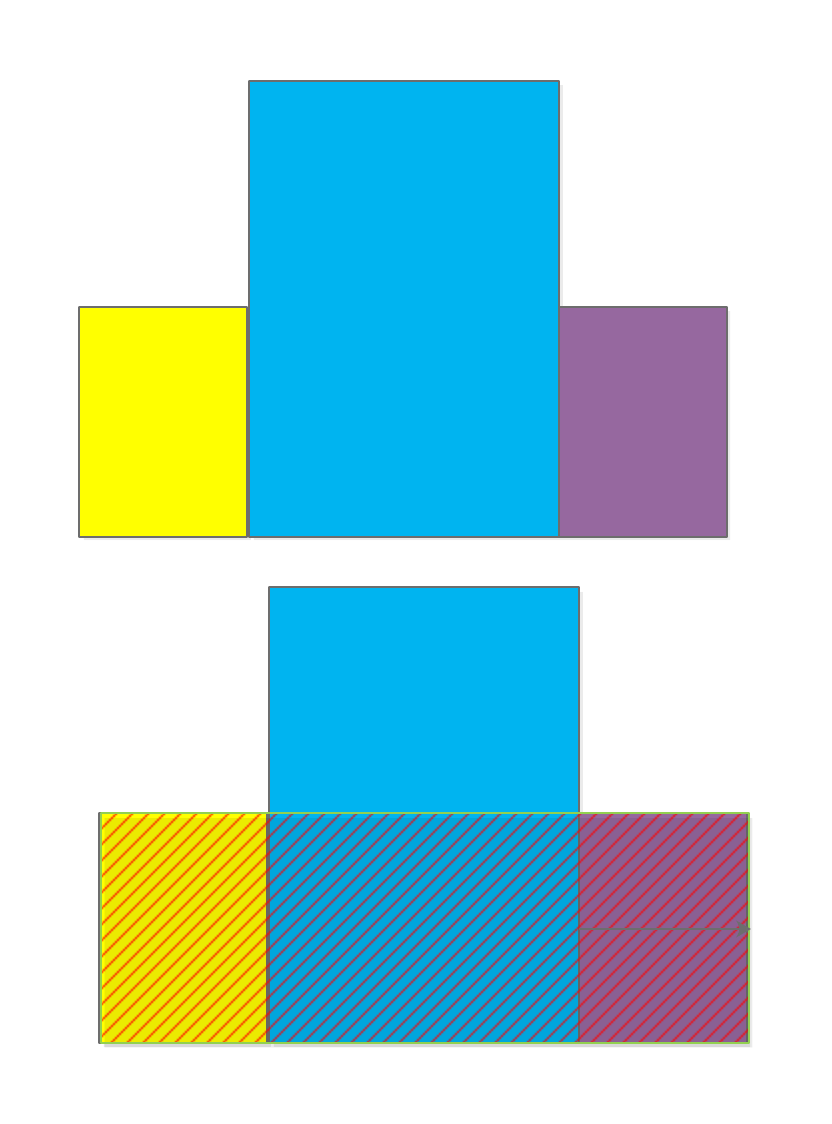
对于这三个矩形，红色阴影矩形即为最大。

不妨先跟书上的例题做个比较，例题中矩形的宽都是1:

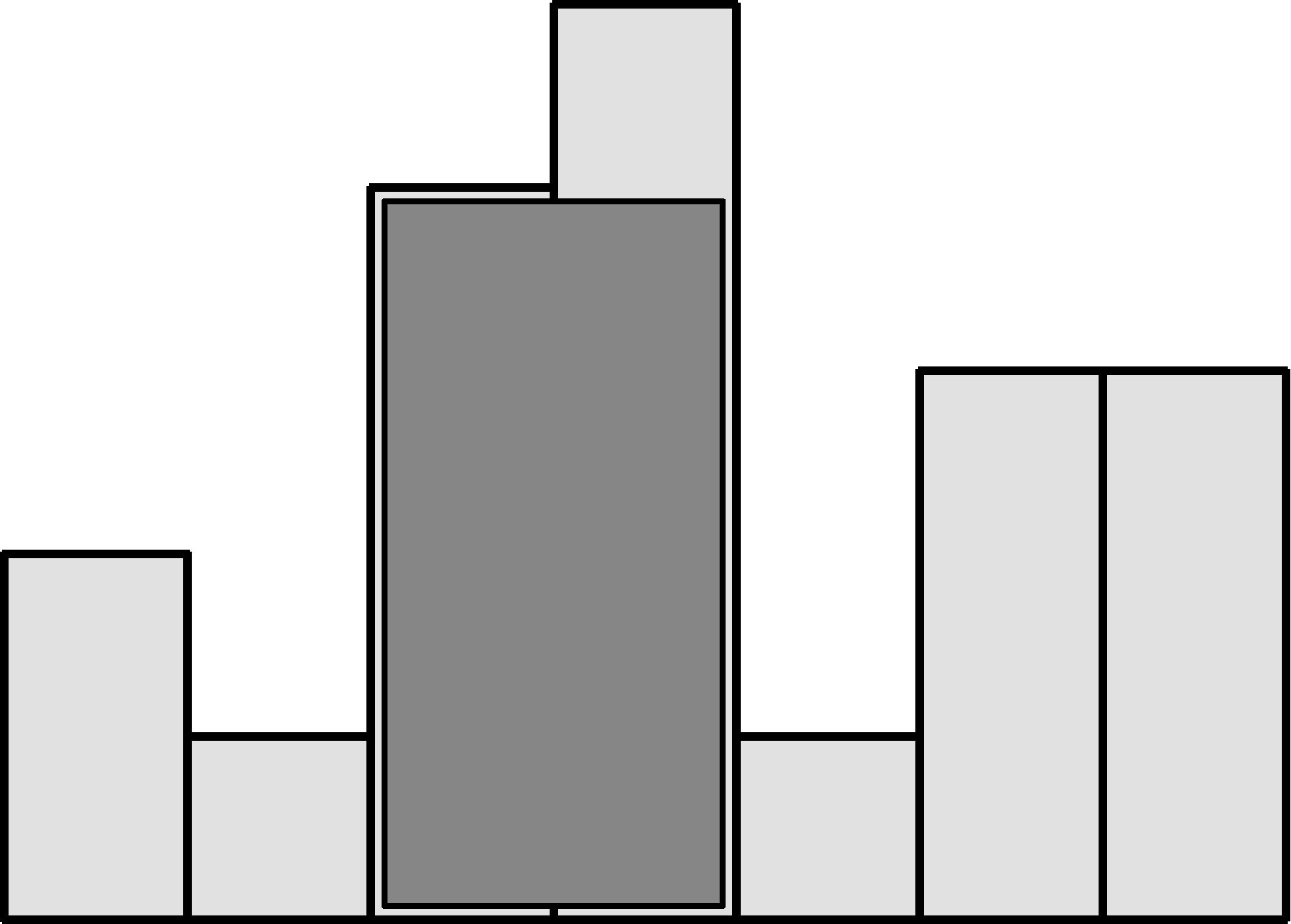
所以在出结果的时候只需

res = max(res, (long long)h[i] * (R[i] - L[i]));

R[i] – L[i]就能得到最终矩形的宽度，如果我们将题目中的宽度与R和L对应起来，比如说用宽度的累计数组代替：

res = max(res, (long long) h[i] * (w_sum[R[i]] - w_sum[L[i]]));

就能直接用书上的模板解题了。

书上例题

复习一下书上的思想：

设面积最大的长方形的左端是L，右端是R，高度是H。如果h_L-1≥H，那么左端点就可以更新为L-1，从而可以得到更大的长方形。这与假设矛盾，因此L是的最大的j，R是的最小的j(>i)。我们把这两个值分别表示为L[i]和R[i]。则

L[i]=(j≤i并且h_j-1<h_i的最大的j) 

R[i]=(j>i并且h_j>h_i的最小的j)

如果能求出L[i]和R[i]，那么最大的面积就是max{hi×(R[i]-L[i])|0≤i

设在栈里的元素从上到下的值为xi，则xi>xi+1且

在计算L[i]时，首先，当栈顶的元素j满足hj≥hi，则不断取出栈顶元素。若栈为空，则L[i]=0，若hj<hi，则L[i]=j+1。然后把i压入栈中。

重点是维护一个单调递减栈，于是改改就过了

#include <iostream>
using namespace std;

#define MAX_N 50000
// 输入
int N;
int w[MAX_N], h[MAX_N];
int w_sum[MAX_N + 1];

int L[MAX_N], R[MAX_N];
int st[MAX_N];  // 栈

void solve()
{
    // 计算L
    int t = 0;  // 栈的大小
    for (int i = 0; i < N; i++)
    {
        while (t > 0 && h[st[t - 1]] >= h[i])
            t--;
        L[i] = t == 0 ? 0 : (st[t - 1] + 1);
        st[t++] = i;
    }

    // 计算R
    t = 0;
    for (int i = N - 1; i >= 0; i--)
    {
        while (t > 0 && h[st[t - 1]] >= h[i])
            t--;
        R[i] = t == 0 ? N : st[t - 1];
        st[t++] = i;
    }

    long long res = 0;  // 注意防止溢出
    for (int i = 0; i < N; i++)
    {
        res = max(res, (long long) h[i] * (w_sum[R[i]] - w_sum[L[i]]));
    }
    printf("%lld\n", res);
}

int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    while (~scanf("%d", &N) && N >= 0)
    {
        for (int i = 0; i < N; ++i)
        {
            scanf("%d%d", w + i, h + i);
            w_sum[i + 1] = w_sum[i] + w[i];
        }
        solve();
    }

#ifndef ONLINE_JUDGE
    fclose(stdin);
#endif
    return 0;
}

一发入魂，真痛快。

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 2082 Terrible Sets​ 题解《挑战程序设计竞赛》