POJ 3494 Largest Submatrix of All 1’s​ 题解《挑战程序设计竞赛》

POJ 3494 Largest Submatrix of All 1’s 

最大子矩阵：给定M*N的01矩阵，求元素最多且都是1的子矩阵。

4.4常用技巧精选（二） 

栈 

还是先来跟书上的例题做个对比，借鉴思路。书上的矩形宽为1，底部对齐：

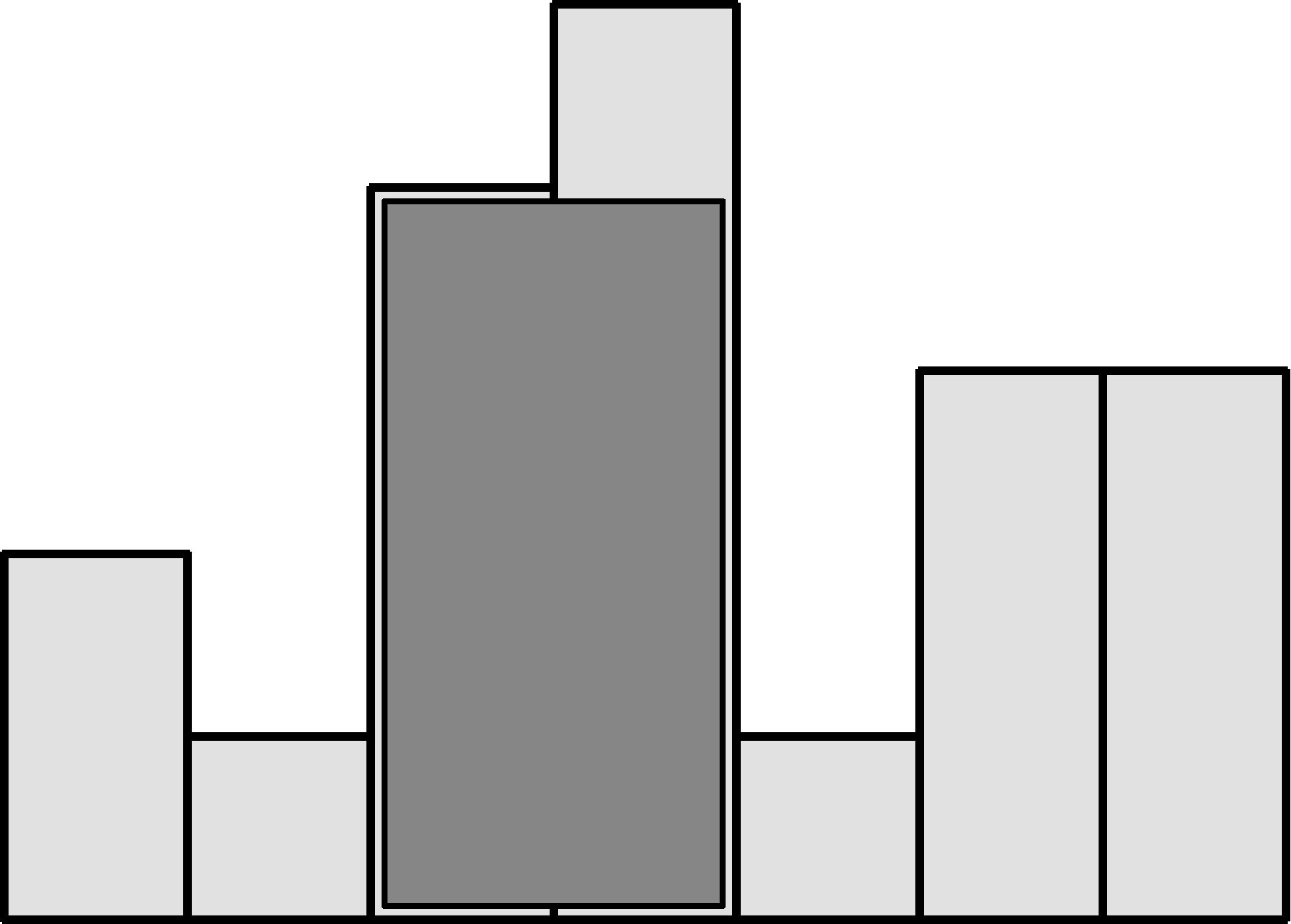
在本题中，将每列中连续的1视作一个宽为1的矩形，就跟例题很像了，只不过底部没有对齐而已。如果我们逐行截断处理，则可视作底部对齐，则每一行构成的子问题都与例题完全一致，取子问题的最大解即为本题的解。

#include <iostream>

using namespace std;

#define MAX_N 2000 + 16
// 输入
int M, N;
int h[MAX_N];

int L[MAX_N], R[MAX_N];
int st[MAX_N];  // 栈

int solve()
{
    // 计算L
    int t = 0;  // 栈的大小
    for (int i = 0; i < N; i++)
    {
        while (t > 0 && h[st[t - 1]] >= h[i])
            t--;
        L[i] = t == 0 ? 0 : (st[t - 1] + 1);
        st[t++] = i;
    }

    // 计算R
    t = 0;
    for (int i = N - 1; i >= 0; i--)
    {
        while (t > 0 && h[st[t - 1]] >= h[i])
            t--;
        R[i] = t == 0 ? N : st[t - 1];
        st[t++] = i;
    }

    int res = 0;  // 注意防止溢出
    for (int i = 0; i < N; i++)
    {
        res = max(res, h[i] * (R[i] - L[i]));
    }
    return res;
}

int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    while (~scanf("%d%d", &M, &N))
    {
        int ans = 0;
        for (int i = 0; i < N; ++i)
        {
            for (int j = 0; j < M; ++j)
            {
                int x;
                scanf("%d", &x);
                h[j] = x ? h[j] + 1 : 0;
            }
            ans = max(ans, solve());
        }
        printf("%d\n", ans);
    }

#ifndef ONLINE_JUDGE
    fclose(stdin);
#endif
    return 0;
}

又是一发入魂

例题、这题与《POJ 2082 Terrible Sets》可以构成一个系列，能够有效地训练观察力，直达不同问题的同一本质。

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 3494 Largest Submatrix of All 1’s​ 题解《挑战程序设计竞赛》