POJ 2114 Boatherds 题解《挑战程序设计竞赛》

POJ 2114 Boatherds 

漂流：给定一颗树及各边长度，请快速查询是否有距离为k的顶点对。

4.6划分、解决、合并：分治法 

树上的分治法 

与POJ1741类似

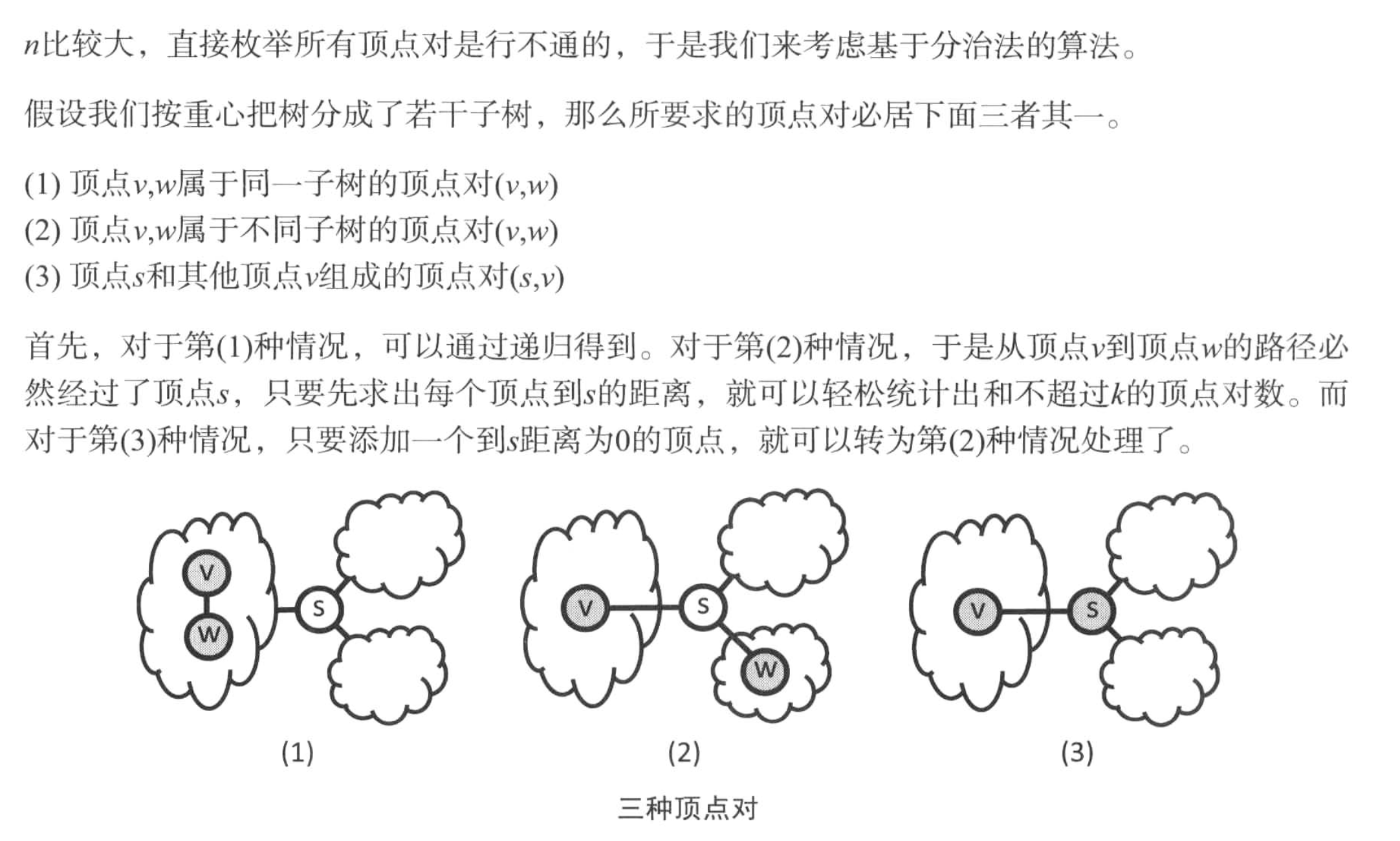
只需将“不超过k”改为“不超过k减去小于k”，就可以得到“等于k”的数量了。

int count_pairs(vector<int> &ds)
{
    int res = 0;
    sort(ds.begin(), ds.end());
    int j = ds.size();
    for (int i = 0; i < ds.size(); i++)
    {
        while (j > 0 && ds[i] + ds[j - 1] > k)
            j--;
        res += j - (j > i ? 1 : 0);//除去和本身组成的点对
    }
    j = ds.size();
    for (int i = 0; i < ds.size(); i++)
    {
        while (j > 0 && ds[i] + ds[j - 1] >= k)
            j--;
        res -= j - (j > i ? 1 : 0);//除去和本身组成的点对
    }
    return res;
}

书上的模板不太给力，能跑对CTU Open 2004，但在POJ上一直TLE。

后来给两个vector加个static就过了，依然这么洒脱

#include <iostream>
#include <vector>
#include <cstdio>
#include <utility>
#include <algorithm>
#include <cstring>

using namespace std;
const int MAX_N = 10000 + 10;
#define INF 0x3f3f3f3f

struct edge
{
    int to, length;
};
vector<edge> G[MAX_N];
int n, k;
bool centroid[MAX_N];//顶点是否已作为重心删除的标记
int subtree_size[MAX_N];//以该顶点为根的子树的大小(查找重心时用)
int ans;//答案

//计算子树大小(subtree_size)的递归函数
int compute_subtree_size(int v, int p)
{
    int c = 1;
    for (int i = 0; i < G[v].size(); i++)
    {
        int w = G[v][i].to;
        if (w == p || centroid[w])
            continue;
        c += compute_subtree_size(G[v][i].to, v);
    }
    subtree_size[v] = c;
    return c;
}

//查找重心的递归函数，t是整个连通分量的大小
//在以v为根的子树中寻找一个顶点，使得删除该顶点后最大子树的顶点数最小
//返回值为pair(最大子树的顶点数，顶点编号)
pair<int, int> search_centroid(int v, int p, int t)
{
    pair<int, int> res = make_pair(INF, -1);
    //s是以v为根的子树的大小
    //m是删除v后最大子树的顶点数
    int s = 1, m = 0;
    for (int i = 0; i < G[v].size(); i++)
    {
        int w = G[v][i].to;
        if (w == p || centroid[w])
            continue;

        res = min(res, search_centroid(w, v, t));

        m = max(m, subtree_size[w]);
        s += subtree_size[w];
    }
    m = max(m, t - s);
    res = min(res, make_pair(m, v));
    return res;
}

//计算子树中的所有顶点到重心的距离
void enumerate_paths(int v, int p, int d, vector<int> &ds)
{
    ds.push_back(d);
    for (int i = 0; i < G[v].size(); i++)
    {
        int w = G[v][i].to;
        if (w == p || centroid[w])
            continue;
        enumerate_paths(w, v, d + G[v][i].length, ds);
    }
}

//统计和不超过K的顶点对的个数
int count_pairs(vector<int> &ds)
{
    int res = 0;
    sort(ds.begin(), ds.end());
    int j = ds.size();
    for (int i = 0; i < ds.size(); i++)
    {
        while (j > 0 && ds[i] + ds[j - 1] > k)
            j--;
        res += j - (j > i ? 1 : 0);//除去和本身组成的点对
    }
    j = ds.size();
    for (int i = 0; i < ds.size(); i++)
    {
        while (j > 0 && ds[i] + ds[j - 1] >= k)
            j--;
        res -= j - (j > i ? 1 : 0);//除去和本身组成的点对
    }
    return res;
}

//对顶点v的子树，查找重心并分割求解的递归函数
void solve_subproblem(int v)
{
    //查找重心s
    compute_subtree_size(v, -1);
    int s = search_centroid(v, -1, subtree_size[v]).second;
    centroid[s] = true;

    //统计按顶点s分割后子树中的对数
    for (int i = 0; i < G[s].size(); i++)
    {
        if (centroid[G[s][i].to])
            continue;
        solve_subproblem(G[s][i].to);
    }

    //统计经过点s的对数
    static vector<int> ds;
    ds.clear();
    ds.push_back(0);
    for (int i = 0; i < G[s].size(); i++)
    {
        if (centroid[G[s][i].to])
            continue;

        static vector<int> tds;
        tds.clear();
        enumerate_paths(G[s][i].to, s, G[s][i].length, tds);

        ans -= count_pairs(tds);
        ds.insert(ds.end(), tds.begin(), tds.end());
    }
    ans += count_pairs(ds);
    centroid[s] = false;
}

void solve()
{
    ans = 0;
    solve_subproblem(0);
}

int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
#endif
    while (~scanf("%d", &n) && n)
    {
        for (int i = 0; i < n; i++)
        {
            G[i].clear();
        }
        for (int u = 0; u < n; u++)
        {
            int v, w;
            while (~scanf("%d", &v) && v)
            {
                --v;
                scanf("%d", &w);
                G[u].push_back((edge) {v, w});
                G[v].push_back((edge) {u, w});
            }
        }
        while (~scanf("%d", &k) && k)
        {
            memset(centroid, 0, sizeof(centroid));
            solve();
            puts(ans > 0 ? "AYE" : "NAY");
        }
        puts(".");
    }
#ifndef ONLINE_JUDGE
    fclose(stdin);
    fclose(stdout);
#endif
    return 0;
}

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 2114 Boatherds 题解《挑战程序设计竞赛》