UVa 12161 Ironman Race in Treeland 题解《挑战程序设计竞赛》

UVa 12161 Ironman Race in Treeland 

赛车：给定一颗树及各边长度及花费，请计算花费在m以内的最长路径。

4.6划分、解决、合并：分治法 

树上的分治法 

不断根据重心分割子树，将包含子树根节点的路径记录到path中。记已经处理过的路径集合为b，未处理的路径集合为e。那么经过子树根节点的路径一定部分来自b，另一部分来自e。

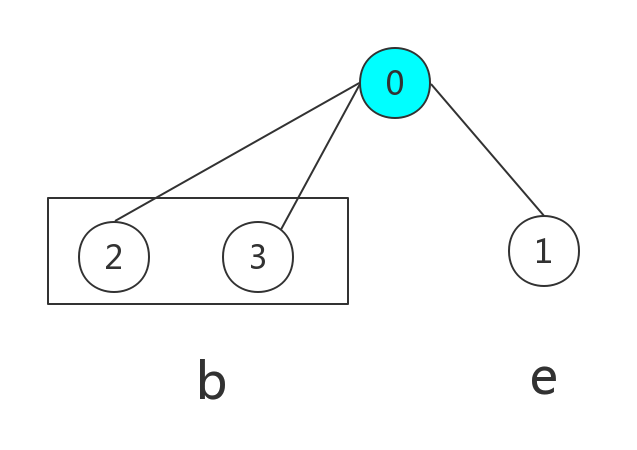
然后设法遍历组合b和e即可。直接枚举并不现实，对b和e分别按花费排序，删除那些花费大长度反而小的路径。那么固定b中的一个元素，e中倒数第一个使得b+e花费不超过m的路径组合即为子树的答案。

书上的模板太坑爹了，光重心分割别的什么都不做提交上去都TLE。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>

using namespace std;
#define MAX_N 30004

struct edge
{
    int to, damage, length, next;
};
int G[MAX_N], edge_size, n, m;
edge E[MAX_N * 2];

void add_edge(int from, int to, int damage, int length)
{
    edge e = {to, damage, length, G[from]};
    E[edge_size] = e;
    G[from] = edge_size++;
}

int ans, pre_max_subtree_size, pre_subtree_size;
int subtree_size[MAX_N];
bool V[MAX_N];

//查找重心的递归函数
//在以v为根的子树中寻找一个顶点，使得删除该顶点后最大子树的顶点数最小
void search_centroid(int v, int p, int &root)
{
    int max_subtree_size = 0;
    subtree_size[v] = 1;
    for (int j = G[v]; ~j; j = E[j].next)
    {
        int to = E[j].to;
        if (to == p || V[to])
            continue;
        search_centroid(to, v, root);
        if (subtree_size[to] > max_subtree_size)
            max_subtree_size = subtree_size[to];
        subtree_size[v] += subtree_size[to];
    }
    if (pre_subtree_size - subtree_size[v] > max_subtree_size)
        max_subtree_size = pre_subtree_size - subtree_size[v];
    if (max_subtree_size < pre_max_subtree_size)
        root = v, pre_max_subtree_size = max_subtree_size;
}

//计算子树大小(subtree_size)的递归函数
int compute_subtree_size(int v, int p)
{
    int ans = 1;
    for (int j = G[v]; ~j; j = E[j].next)
    {
        int to = E[j].to;
        if (to == p || V[to])
            continue;
        ans += compute_subtree_size(to, v);
    }
    return ans;
}

pair<int, int> path[MAX_N];
int b, e;

//计算子树中的所有顶点到重心的距离
void enumerate_paths(int v, int p, int damage, int length)
{
    path[e++] = {damage, length};
    for (int j = G[v]; ~j; j = E[j].next)
    {
        int to = E[j].to;
        if (to == p || V[to])
            continue;
        if (damage + E[j].damage <= m)
        {
            enumerate_paths(to, v, damage + E[j].damage, length + E[j].length);
        }
    }
}

// 删除长度小，花费大的路径
void remove_useless(int b, int &e)
{
    if (b == e)
        return;
    int size;
    for (int i = size = b + 1; i < e; i++)
    {
        if (path[i].first == path[size - 1].first)
            continue;
        if (path[i].second <= path[size - 1].second)
            continue;
        path[size++] = path[i];
    }
    e = size;
}

void solve_sub_problem(int v, int p)
{
    for (int j = G[v]; ~j; j = E[j].next)
    {
        int to = E[j].to;
        if (to == p || V[to])
            continue;
        pre_max_subtree_size = MAX_N;
        pre_subtree_size = compute_subtree_size(to, v);
        int root;
        search_centroid(to, v, root);
        V[root] = 1;
        solve_sub_problem(root, v);
        V[root] = 0;
    }
    b = e = 0;
    for (int j = G[v]; ~j; j = E[j].next)
    {
        int to = E[j].to;
        if (to == p || V[to])
            continue;
        if (E[j].damage <= m)
        {
            enumerate_paths(to, v, E[j].damage, E[j].length);
        }
        if (b > 0)
        {
            sort(path + b, path + e);
            remove_useless(b, e);
            for (int b_ = 0, e_ = e - 1; b_ < b; b_++)
            {
                while (e_ >= b && path[b_].first + path[e_].first > m)
                    e_--;
                if (e_ >= b)
                    ans = max(ans, path[b_].second + path[e_].second);
            }
        }
        sort(path, path + e);
        remove_useless(0, e);
        b = e;
    }
}

int solve()
{
    int root;
    pre_max_subtree_size = MAX_N, pre_subtree_size = n;
    search_centroid(1, -1, root);
    V[root] = 1;
    solve_sub_problem(root, -1);
    return ans;
}

int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
    freopen("err.txt", "w", stderr);
#endif
    int T, t = 1;
    scanf("%d", &T);
    while (T--)
    {
        ans = 0;
        edge_size = 0;
        memset(G, -1, sizeof(G));
        memset(V, 0, sizeof(V));
        scanf("%d%d", &n, &m);
        for (int i = 0; i < n - 1; i++)
        {
            int u, v, damage, length;
            scanf("%d%d%d%d", &u, &v, &damage, &length);
            --u, --v;
            add_edge(u, v, damage, length);
            add_edge(v, u, damage, length);
        }
        printf("Case %d: %d\n", t++, solve());
    }
#ifndef ONLINE_JUDGE
    fclose(stdin);
    fclose(stderr);
#endif
    return 0;
}

Reference

https://github.com/pkkj/ACM-ICPC-OJ-Code/blob/344b2c92f75b428d0241ba732c43de780d08df40/ICPC.Regional/2008.Kuala_Lumpur/2008.Kuala_Lumpur.Solution_CN.md#problem-g-ironman-race-in-treeland

 知识共享署名-非商业性使用-相同方式共享：码农场 » UVa 12161 Ironman Race in Treeland 题解《挑战程序设计竞赛》