POJ 3109 Inner Vertices 题解 《挑战程序设计竞赛》

POJ 3109 Inner Vertices

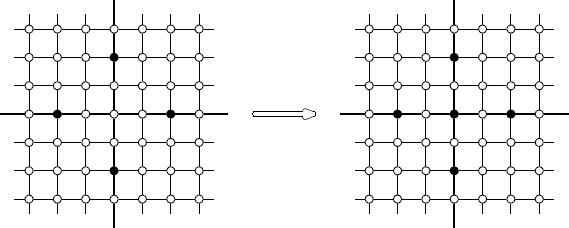
黑白棋・改：无限大的棋盘上，在横向和纵向上被包围的白子会变成黑子，求最终黑子个数？

3.3活用各种数据结构

Binary Indexed Tree

首先需要了解一下扫描线算法，扫描线算法是计算几何学上对多边形染色的算法。

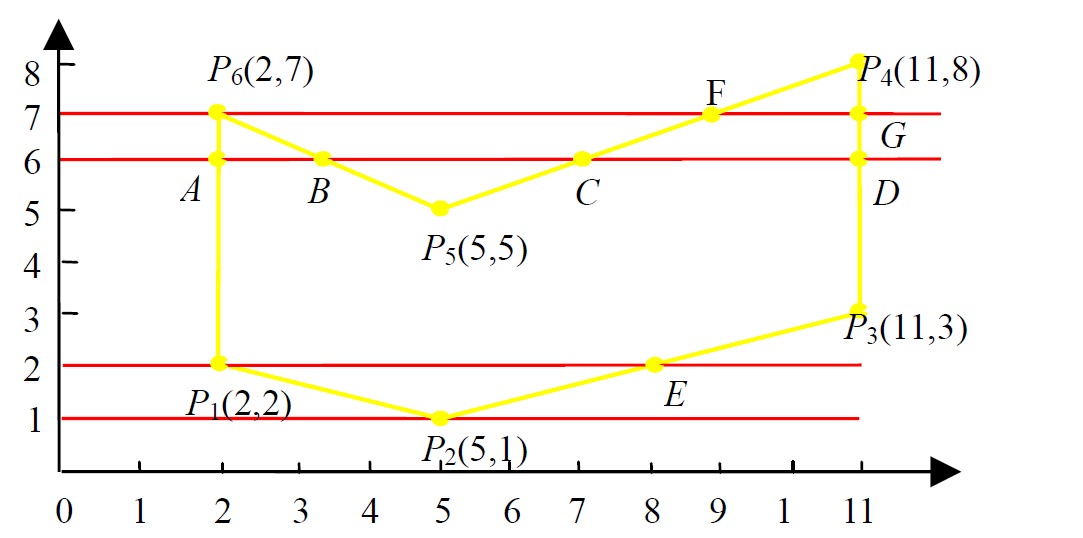
如图，扫描线算法的目标是计算黄颜色多边形内部的像素点，最终将其涂色。怎么知道哪些点在内部呢？首先从顶点中y轴最小坐标出发，到最大坐标为止，画一条条水平的扫描线，扫描线必然与多边形有多个交点。第一个与第二个，第三个与第四个……之间的点就是内部点。

用严密的语言描述如下：

基本思想

        按扫描线顺序，计算扫描线与多边形的相交区间，再用要求的颜色显示这些区间的象素，即完成填充工作。

对于一条扫描线填充过程可以分为四个步骤：

    (1)  求交：计算扫描线与多边形各边的交点

    (2)  排序：把所有交点按 x 坐标递增顺序来排序

    (3)  配对：确定扫描线与多边形的相交区间，第一个与第二个，第三个与第四个等等，每对交点代表扫描线与多边形的一个相交区间

    (4)  填充：显示相交区间的象素

回到题目，题目给的是一张无限大的棋盘，所以需要先进行坐标压缩，压缩之后采取扫描线法计算内部点数即可。

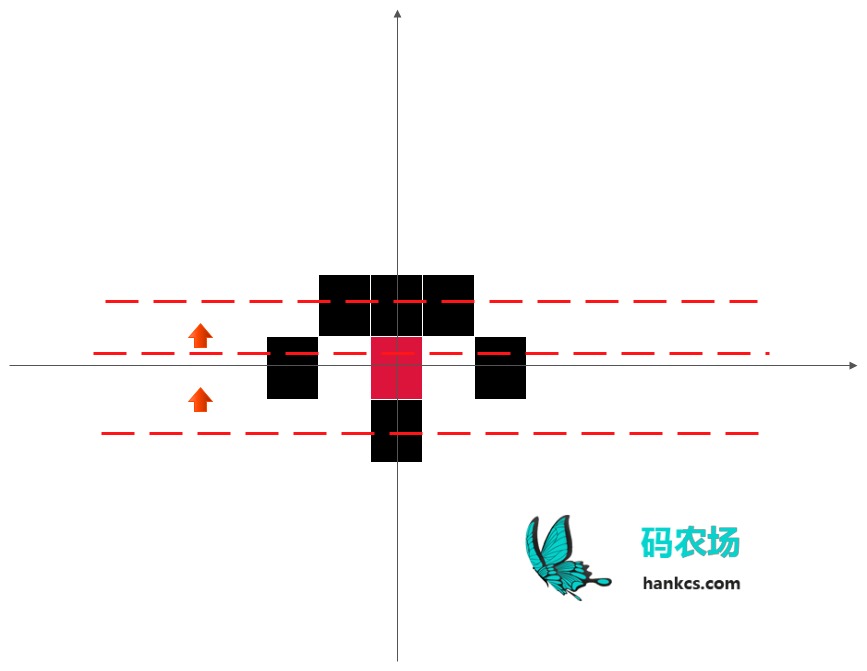
上图红色方格即为要染色的点，计算两个交点之间的空白点的数量的时候，由于它们的Y坐标肯定相等，那么问题转化为统计两个交点x坐标之间的点的个数。涉及到累积和，轮到树状数组出场了。

统计x的时候，需要将一个区间[交点n的x + 1，交点n+1的x – 1]的个数统统加一，树状数组本身做加法的话是logn，做n次的话是nlogn，太浪费了，BIT可以高效地求一段区间和，以及更新单个元素的值，但是无法高效地更新一个区间的值。

于是可以用双BIT来实现，一个维护初始个数，一个维护累加值，可以将复杂度控制在logn。

具体说来，可以用如下方式定义这两个BIT：bit0和bit1

其中bit1表示增量的累计和，如图：

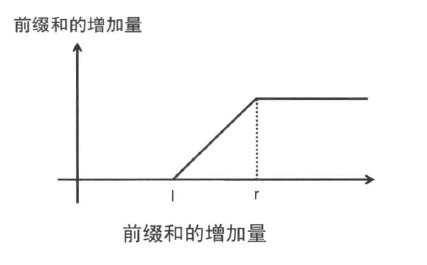
对区间[l,r]增加x之后，前缀和的增量如上图所示。我们用bit1来维护每个元素的增加量，当然，执行add(i,x)后并不是每个元素都会改变，所以还需要用sum(bit0,i)来维护初始值的修正值。准确来说，只有l和r之间的元素才会+x，所以表示增加量的bit1[l] += x，bit1[r + 1] += -x（这里的思想和imos法是一致的，记录变化量，然后累加），假设i<l，这次add不影响sum。假设i位于l和r之间，sum(bit1,i)*i = xi，xi的意思是前i个元素每个都+x，看起来比正确答案多加了(1-l)*x的样子，所以修正值bit0必须执行bit0[l]=-(l-1)*x。假设i>r，表示增加量的sum(bit1,i)根本没发生变化（因为l位置的x和r+1位置的-x抵消掉了），这时候就得依靠bit0在r+1位置的xr减去l位置的x(l-1)得出正确答案x(r-l+1)作为最终的结果了。

这样子就可以理解上面的4个操作的由来了。嘛，尽量理解吧。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
#define MAX_N 100000 + 16
typedef long long LL;

LL bit0[MAX_N], bit1[MAX_N];	// 双BIT实现O(logn)区间加法
int N, X[MAX_N], Y[MAX_N];
vector<int> line[MAX_N];	// 每个黑子构成的一条条水平线，y坐标作为下标
bool visited[MAX_N];		// 是否已经算过了


// 求和sum{a[t], 0 <= t <= i}
LL sum(LL *b, int i)
{
	int s = 0;
	while (i > 0) 
	{
		s += b[i];
		i -= (i & -i);
	}
	return s;
}

// 求和a[from, to)
LL sum(LL* bit, int from, int to)
{
	return sum(bit, to - 1) - sum(bit, from - 1);
}

// 执行 a[i] += v
void add(LL *b, int i, LL v)
{
	while (i <= MAX_N)
	{
		b[i] += v;
		i += (i & -i);
	}
}
// 基础bit结束

// 双BIT

//[0,n]
LL sum(int i)
{
	return sum(bit1, i) * i + sum(bit0, i);
}

//(from, to]
LL sum(int from, int to)
{
	return sum(to) - sum(from);
}

// [from, to]
void add(int from, int to, LL x)
{
	add(bit0, from, -x * (from - 1));
	add(bit1, from, x);
	add(bit0, to, x * to);
	add(bit1, to, -x);
}

// 压缩坐标，将坐标的值变成“这是第几种值”，返回一共有几种坐标
// x为坐标数组，长度为N
int compress(int *p)
{
	vector<int> ps(N);

	for (int i = 0; i < N; ++i)
	{
		ps[i] = p[i];
	}

	sort(ps.begin(), ps.end());
	ps.erase(unique(ps.begin(), ps.end()), ps.end());
	for (int i = 0; i < N; ++i)
	{
		p[i] = 1 + distance(ps.begin(), lower_bound(ps.begin(), ps.end(), p[i]));	// 此处加1为了防止 i += (i & -i); 永远为0
	}
	return ps.size();
}

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
#endif
	scanf("%d", &N);
	for (int i = 0; i < N; ++i)
	{
		scanf("%d%d", X + i, Y + i);
	}
	int w = compress(X);
	int h = compress(Y);

	for (int i = 0; i < N; ++i)
	{
		line[Y[i]].push_back(X[i]);	// 一条条扫描线
	}

	LL result = N;
	for (int y = 1; y <= h; ++y)
	{
		// 对每条扫描线，计算上面空白点的个数
		vector<int>& xs = line[y];	// 纵坐标为y的那些点的横坐标，一条扫描线
		sort(xs.begin(), xs.end());
		
		for (vector<int>::iterator i = xs.begin(); i != xs.end(); ++i)
		{
			int x = *i;
			LL s = sum(x - 1, x);	// 横坐标为x的空白点个数

			if (visited[x])
			{
				result += s;		// 就是要染色的像素点
			}
			else
			{
				visited[x] = true;
			}
			add(bit0, x, -s);		// 等同于add(x, x, -s);即对count[x] -= s；这是一个复位操作，为下次统计做准备
			if (i + 1 != xs.end())
			{
				// 到下一个黑点之间空白点的个数
				// 这两个分支合并起来就是 add(x + 1, next_x - 1, 1);的意思
				if (x + 1 < *(i + 1) - 1)			// 下一个黑子
				{
					add(x + 1, *(i + 1) - 1, 1);	// 遇到了空白
				}
				else if (x + 1 == *(i + 1) - 1)
				{
					add(bit0, x + 1, 1);			// 遇到了空白,此时等同于add(x + 1, x + 1, 1);
				}
			}
		}
	}
	cout << result << endl;
#ifndef ONLINE_JUDGE
	fclose(stdin);
	fclose(stdout);
	system("out.txt");
#endif
	return 0;
}
///////////////////////////End Sub//////////////////////////////////

 知识共享署名-非商业性使用-相同方式共享：码农场 » POJ 3109 Inner Vertices 题解 《挑战程序设计竞赛》