![]() 本文是《统计学习方法》第4章的笔记,用图形补充说明了条件概率分布计算时可能引发的维数灾难,在文末用Python实现了一个基于贝叶斯文本分类器的简单情感极性分析器,可以分析中文句子的情感极性。
本文是《统计学习方法》第4章的笔记,用图形补充说明了条件概率分布计算时可能引发的维数灾难,在文末用Python实现了一个基于贝叶斯文本分类器的简单情感极性分析器,可以分析中文句子的情感极性。
朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。训练的时候,学习输入输出的联合概率分布;分类的时候,利用贝叶斯定理计算后验概率最大的输出。
朴素贝叶斯法的学习与分类
基本方法
设输入空间 为n维向量的集合,输出空间为类标记集合
为n维向量的集合,输出空间为类标记集合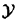 ={c1……ck}。输入特征向量x和输出类标记y分属于这两个集合。X是输入空间上的随机变量,Y是输出空间上的随机变量。P(X,Y)是X和Y的联合概率分布,训练数据集
={c1……ck}。输入特征向量x和输出类标记y分属于这两个集合。X是输入空间上的随机变量,Y是输出空间上的随机变量。P(X,Y)是X和Y的联合概率分布,训练数据集
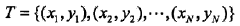
由P(X,Y)独立同分布产生。
朴素贝叶斯法通过T学习联合概率分布P(X,Y)。具体来讲,学习以下先验概率:
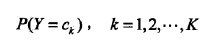
以及条件概率分布:
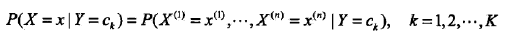
于是根据联合概率分布密度函数:
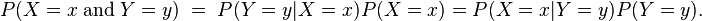
学习到联合概率分布P(X,Y)。
而条件概率分布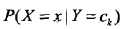 的参数数量是指数级的,也就是X和Y的组合很多,假设xj可能取值Sj个,Y可能取值有K个,那么参数的个数是
的参数数量是指数级的,也就是X和Y的组合很多,假设xj可能取值Sj个,Y可能取值有K个,那么参数的个数是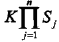 。特别地,取xj=S,那么参数个数为KSn,当维数n很大的时候,就会发生维数灾难。
。特别地,取xj=S,那么参数个数为KSn,当维数n很大的时候,就会发生维数灾难。
豆知识:维数灾难
一维空间中,把一个单位空间(退化为区间)以每个点距离不超过0.01采样,需要102个平均分布的采样点,而在10维度空间中,需要1020个点才行。计算方式用Python描述如下:
dimensionality = 10 print 1 / (0.01 ** dimensionality)
也可以如下可视化:
# -*- coding:utf-8 -*- # Filename: dimensionality.py # Author:hankcs # Date: 2015/2/6 14:40 from matplotlib import pyplot as plt import numpy as np max_dimensionality = 10 ax = plt.axes(xlim=(0, max_dimensionality), ylim=(0, 1 / (0.01 ** max_dimensionality))) x = np.linspace(0, max_dimensionality, 1000) y = 1 / (0.01 ** x) plt.plot(x, y, lw=2) plt.show()
可视化图像:
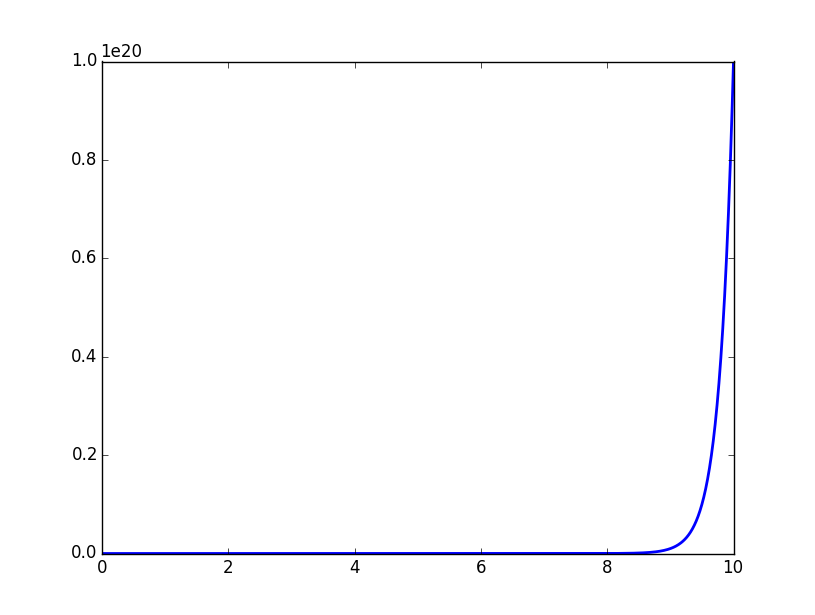
这种指数级的复杂度增长被称为维数灾难。
看完这个图大概就能理解为什么条件概率分布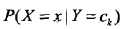 无法计算了。
无法计算了。
为了计算它,朴素贝叶斯法对它做了条件独立性的假设:
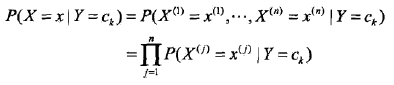
也就是各个维度的特征在类确定的情况下都是独立分布的。这一假设简化了计算,也牺牲了一定的分类准确率。
基于此假设,以及贝叶斯定理,后验概率为:
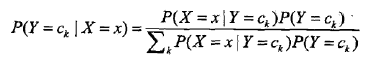
分母其实是P(X=x),等同于枚举ck求联合分布的和:∑P(X=x,Y=ck),此联合分布按公式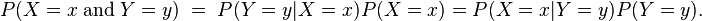 拆开,等于上式分母。
拆开,等于上式分母。
将独立性假设代入上式,得到:
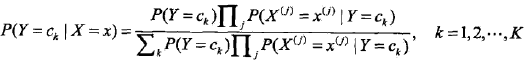
朴素贝叶斯分类器可以表示为:
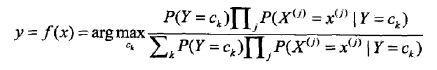
也就是给定参数,找一个概率最大的ck出来。注意到上式分母其实就是P(X=x),x给定了就固定了,跟ck一点关系都没有,所以分母可以去掉,得到:
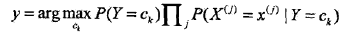
后验概率最大化的含义
选择0-1损失函数:
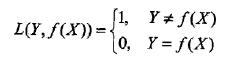
f(X)就是分类器的决策函数,损失函数的参数其实是一个联合分布。
此时期望风险函数为:
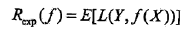
上面说过,这是一个联合分布P(X,Y),是一个and(连乘)的形式,由此取条件期望为风险函数:
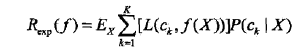
所谓条件期望,就是指X=x时,Y的期望。上式其实可以这么推回去:
Ex∑[L()]P(ck|X)=∑P(X)∑[L()]P(X,ck)/P(X)=∑[L()]P(X,ck)=E[L()]
格式比较乱,但愿意思到了。
为了最小化上式,只需对每个X=x执行最小化,那么加起来肯定是极小化的,由此有:
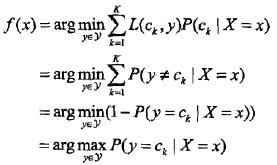
其实不用这么一堆公式,光靠感觉也很好理解,给了一些证据后,不挑后验概率最大的,还能挑啥呢?
朴素贝叶斯法的参数估计
极大似然估计
前面说过,朴素贝叶斯法要学习的东西就是P(Y=ck)和P(X=x|Y=ck),这两个概率的估计用极大似然估计法(简单讲,就是用样本猜测模型参数,或者说使得似然函数最大的参数)进行:
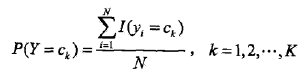
也就是用样本中ck的出现次数除以样本容量。
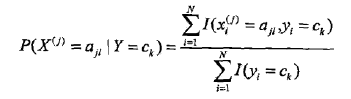
分子是样本中变量组合的出现次数,分母是上面说过的样本中ck的出现次数。
学习与分类算法
于是就有朴素贝叶斯算法,先从训练数据中计算先验概率和条件概率,然后对于给定的实例计算最大的条件概率,输出该条件对应的类别。形式化的描述如下:

例子
给定训练数据:

给x=(2,S)T分类。
这个太简单了,利用(3)中的式子就行了。
贝叶斯估计
最大似然估计有个隐患,假设训练数据中没有出现某种参数和类别的组合怎么办?此时估计的概率值为0,但是这不代表真实数据中就没有这样的组合。解决办法是采用贝叶斯估计
1、条件概率的贝叶斯估计:
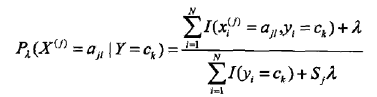
其中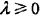 ,Sj表示xj可能取值的种数。分子和分母分别比最大似然估计多了一点东西,其意义是在随机变量每个取值的频数上加一个常量
,Sj表示xj可能取值的种数。分子和分母分别比最大似然估计多了一点东西,其意义是在随机变量每个取值的频数上加一个常量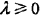 。当此常量取0时,就是最大似然估计,当此常量取1时,称为拉普拉斯平滑。
。当此常量取0时,就是最大似然估计,当此常量取1时,称为拉普拉斯平滑。
2、先验概率的贝叶斯估计:
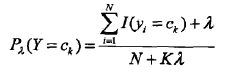
贝叶斯情感极性分析器
书中例题太简单,不过瘾。这里分析一个基于贝叶斯文本分类器实现的简单情感极性分析器。
调用实例:
# -*- coding:utf-8 -*-
# Filename: Bayes.py
# Author:hankcs
# Date: 2015/2/6 22:25
from math import log, exp
class LaplaceEstimate(object):
"""
拉普拉斯平滑处理的贝叶斯估计
"""
def __init__(self):
self.d = {} # [词-词频]的map
self.total = 0.0 # 全部词的词频
self.none = 1 # 当一个词不存在的时候,它的词频(等于0+1)
def exists(self, key):
return key in self.d
def getsum(self):
return self.total
def get(self, key):
if not self.exists(key):
return False, self.none
return True, self.d[key]
def getprob(self, key):
"""
估计先验概率
:param key: 词
:return: 概率
"""
return float(self.get(key)[1]) / self.total
def samples(self):
"""
获取全部样本
:return:
"""
return self.d.keys()
def add(self, key, value):
self.total += value
if not self.exists(key):
self.d[key] = 1
self.total += 1
self.d[key] += value
class Bayes(object):
def __init__(self):
self.d = {} # [标签, 概率] map
self.total = 0 # 全部词频
def train(self, data):
for d in data: # d是[[词链表], 标签]
c = d[1] # c是分类
if c not in self.d:
self.d[c] = LaplaceEstimate() # d[c]是概率统计工具
for word in d[0]:
self.d[c].add(word, 1) # 统计词频
self.total = sum(map(lambda x: self.d[x].getsum(), self.d.keys()))
def classify(self, x):
tmp = {}
for c in self.d: # 分类
tmp[c] = log(self.d[c].getsum()) - log(self.total) # P(Y=ck)
for word in x:
tmp[c] += log(self.d[c].getprob(word)) # P(Xj=xj | Y=ck)
ret, prob = 0, 0
for c in self.d:
now = 0
try:
for otherc in self.d:
now += exp(tmp[otherc] - tmp[c]) # 将对数还原为1/p
now = 1 / now
except OverflowError:
now = 0
if now > prob:
ret, prob = c, now
return (ret, prob)
class Sentiment(object):
def __init__(self):
self.classifier = Bayes()
def segment(self, sent):
words = sent.split(' ')
return words
def train(self, neg_docs, pos_docs):
data = []
for sent in neg_docs:
data.append([self.segment(sent), u'neg'])
for sent in pos_docs:
data.append([self.segment(sent), u'pos'])
self.classifier.train(data)
def classify(self, sent):
return self.classifier.classify(self.segment(sent))
s = Sentiment()
s.train([u'糟糕', u'好 差劲'], [u'优秀', u'很 好']) # 空格分词
print s.classify(u"好 优秀")
输出
(u'pos', 0.6666666666666665)
说明“好优秀”这句话具有正能量的概率是66%,虽然“好”这个词语也存在于负极性的语句中,但是分类器还是准确地区分了它。
上面的贝叶斯分类器使用了拉布拉斯平滑处理策略,在进行条件概率的时候,不是连乘,而是取对数相加,最后逐差取指数,这个过程会发生归一化,得出一个概率出来。
Reference
情感极性分析器主要参考了snownlp的实现。
 码农场
码农场
博主,你好,给出的样例 print s.classify(u”好 优秀”),这个结果应该错了吧,两个正负面训练集数据词频相同,“优秀”虽然不在负面训练集中,但经过拉普拉斯平滑之后,词频为1,所以最终的正负面概率应该是相等的??
45行、48行是否重复加?
def classify(self, x):
tmp = {}
for c in self.d: # 分类
tmp[c] = log(self.d[c].getsum()) – log(self.total) # P(Y=ck)
for word in x:
tmp[c] += log(self.d[c].getprob(word)) #log(关于不同的xj累乘( P(Xj=xj | Y=ck))*P(Y=ck))=log(P(X|Y=ck)*P(Y=ck))=log(P(X,Y=ck))
ret, prob = 0, 0
for c in self.d:
now = 0
try:
for otherc in self.d:
now += exp(tmp[otherc] – tmp[c]) # (关于不同的Y取值ck累加(P(x|Y=ck)*P(Y=ck)))|P(x|Y=ck)*P(Y=ck)=P(X)/P(x,Y=ck)=1/P(Y=ck|X)
now = 1 / now #将对数还原为p(Y=ck|X)
except OverflowError:
now = 0
if now > prob: #不断更新最大概率的类别
ret, prob = c, now
return (ret, prob)
我自己的理解, 不知道对不对
解释一下博主的第74-83行判断分类的代码。
确实可以直接通过直接比较tmp[c]的大小直接判断label。
原代码中的now>prob就是用来寻找最大概率的。
77-81行是用来还原对数得到真实后验概率的,考虑了原公式中分母中的全概率。
不考虑全概率得不到后验概率。
now+=exp(tmp[otherc]-tmp[c])
当otherc=c时,这部分为1。即本身对其本身来说为1。
当otherc!=c时,这部分为x。即otherc对于c来说的相对大小。假设为2。
则判断为标记c的概率为1/3。
博主你好,请教一下,对于朴素贝叶斯问题,可以直接使用最大化后验概率来对给定验证集进行预测;当如果使用最大化后验概率求解问题存在难度时,就可以通过贝叶斯估计分别求出先验概率和条件概率,然后在求解后验概率。这么理解正确吗?也就是说,《统计学习方法》的朴素贝叶斯法这一章中提供两种求解方案?
classify的对数和指数不是为了归一化吧,我记得应该是防止下溢,由于有浮点数计算才用的对数和指数,博主能给解释一下吗?
代码74-83这一段是什么意思呢?
这段搞懂了,这是按照原始的朴素贝叶斯基本公式来做的,但是实际上只需要比较tmp[c]的大小就好了,因为对所有的c,朴素贝叶斯基本公式的分母都是一样的
推出来了。。博主,我刚刚开始研究ml,公式能看懂,但是转化成代码,有些困难,希望你可以给一些建议~
能解释下么
博主,代码里面第78行,是如何推导的啊?推了好久,没弄明白。。
请问,怎么对文本信息进行分类
s = Sentiment()
我想知道的是楼主学概率论和高数么?明明是文科生为什么这些公式理解起来这么轻松啊。。
学是学过,早忘光了,基本现学的。我是个怪物。
真的好牛b,膜拜!!!!