![]() 看完《统计学习方法》后,最近以将近一天一课速度把斯坦福的机器学习公开课看了大半。速度很快但感觉没有《方法》扎实,应该是没有足够的实践所致。正巧最近也在学Matlab,于是把课后的编程练习过一遍,一举两得。
看完《统计学习方法》后,最近以将近一天一课速度把斯坦福的机器学习公开课看了大半。速度很快但感觉没有《方法》扎实,应该是没有足够的实践所致。正巧最近也在学Matlab,于是把课后的编程练习过一遍,一举两得。![]()
目标
作为CS229的第一次编程练习,其主题是线性回归,没什么难度,只是让大家熟悉熟悉matlab而已。任务具体是实现线性规划,以及数据可视化。
说个题外话,斯坦福matlab编程练习的提交方式竟然是利用一个submit.m的matlab函数完成的,果然酷炫吊炸天,跟那些.rar .zip就是不一样。
function submit(partId, webSubmit) %SUBMIT Submit your code and output to the ml-class servers % SUBMIT() will connect to the ml-class server and submit your solution
单变量线性回归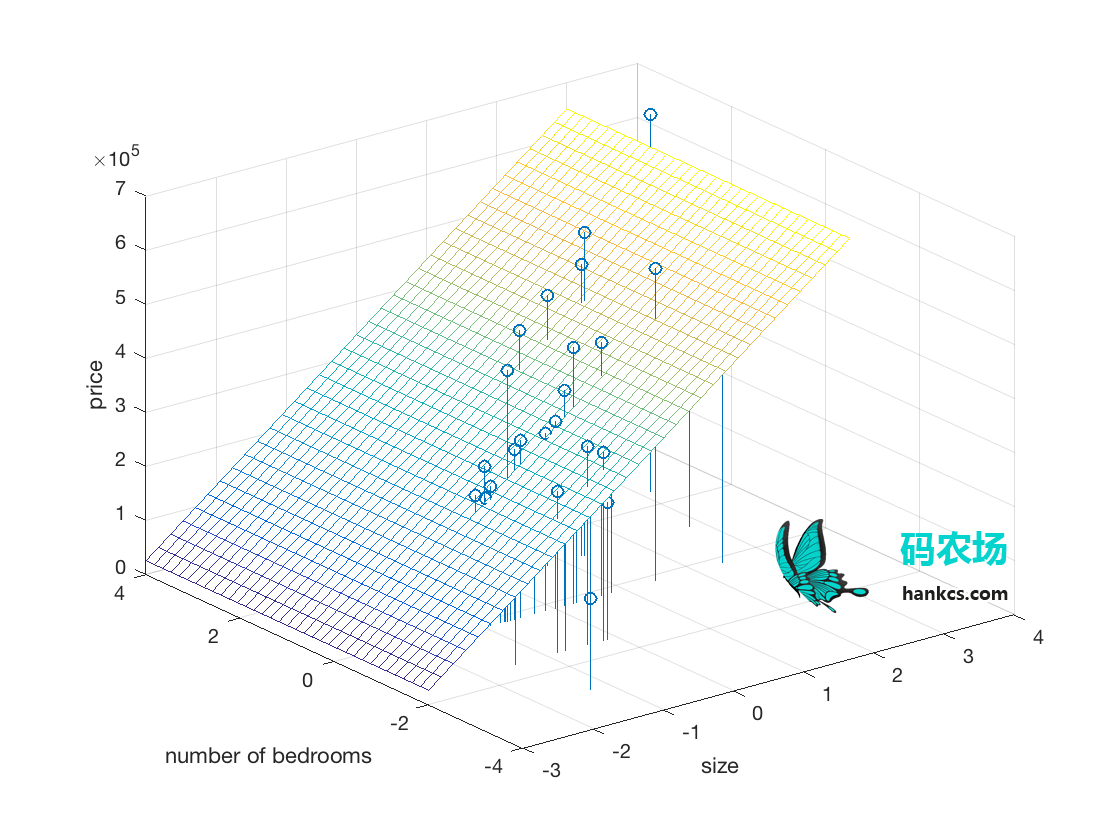
你是一个餐馆老板,想在不同城市开分店。你收集了这些城市的人口数和当地餐馆的利润。请利用线性回归找出它们之间的规律。
数据示例:
6.1101,17.592 5.5277,9.1302 8.5186,13.662 7.0032,11.854 5.8598,6.8233
数据可视化
吴恩达教授的理念是,第一步雷打不动把数据可视化出来。
%% ======================= Part 2: Plotting =======================
fprintf('Plotting Data ...\n')
data = load('ex1data1.txt');
X = data(:, 1); y = data(:, 2);
m = length(y); % number of training examples
% Plot Data
% Note: You have to complete the code in plotData.m
plotData(X, y);
fprintf('Program paused. Press enter to continue.\n');
pause;
Matlab的接口的确做得很简洁,隐藏了很多细节,加载一个矩阵就一句话。
plotData函数:
function plotData(x, y)
%PLOTDATA Plots the data points x and y into a new figure
% PLOTDATA(x,y) plots the data points and gives the figure axes labels of
% population and profit.
% ====================== YOUR CODE HERE ======================
% Instructions: Plot the training data into a figure using the
% "figure" and "plot" commands. Set the axes labels using
% the "xlabel" and "ylabel" commands. Assume the
% population and revenue data have been passed in
% as the x and y arguments of this function.
%
% Hint: You can use the 'rx' option with plot to have the markers
% appear as red crosses. Furthermore, you can make the
% markers larger by using plot(..., 'rx', 'MarkerSize', 10);
figure; % open a new figure window
plot(x,y,'rx','MarkerSize',10); %plot the data
ylabel('Profit in $10,000s'); %set the y-axis label
xlabel('Population of City in 10,000s');%set the x-axis label
title('ex1data1.txt');
% ============================================================
end
绘图接口也很简单,指定数据点颜色、大小、横纵轴,再加个标题。
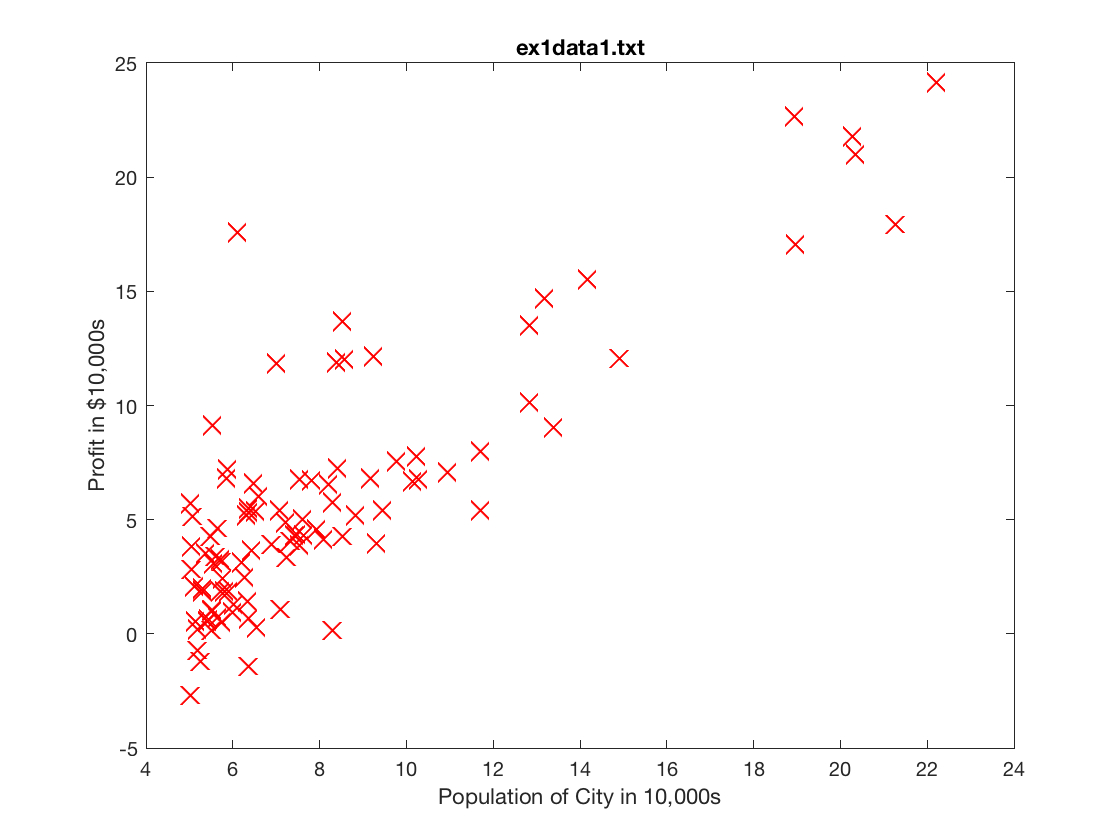
梯度下降
参数更新公式
最小化目标函数
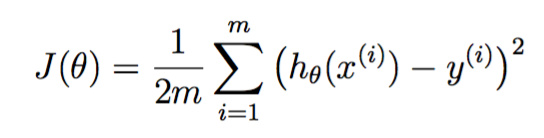
假设函数为
![]()
优化方法为梯度下降
![]()
下标j表示第j个参数。
对目标函数求导
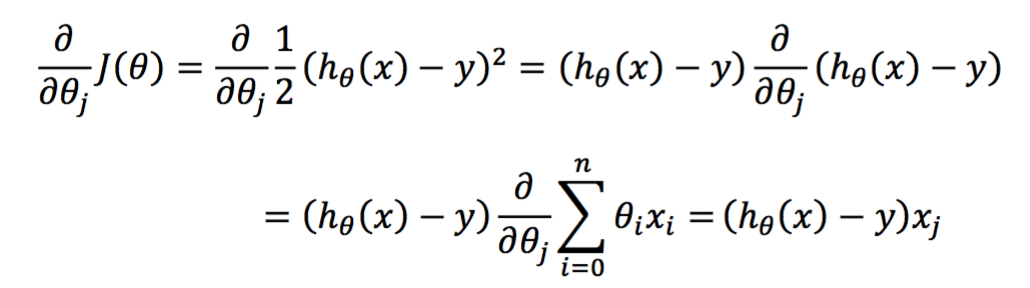
若每次只训练一个实例,则称为最小二乘法
![]()
若每次批量训练所有m个实例,则称为批梯度下降算法
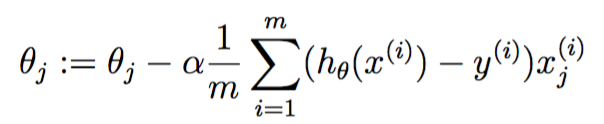
上标i表示第i个实例,对比两种算法,注意后者对每个参数,都同时使用了所有训练实例。
参数
%% =================== Part 3: Gradient descent ===================
fprintf('Running Gradient Descent ...\n')
X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters
% Some gradient descent settings
iterations = 1500;
alpha = 0.01;
指定了迭代次数和学习率,初始化参数为2*1的0向量。
计算损失函数
% compute and display initial cost computeCost(X, y, theta)
其实现如下
function J = computeCost(X, y, theta) %COMPUTECOST Compute cost for linear regression % J = COMPUTECOST(X, y, theta) computes the cost of using theta as the % parameter for linear regression to fit the data points in X and y % Initialize some useful values m = length(y); % number of training examples % You need to return the following variables correctly J = 0; % ====================== YOUR CODE HERE ====================== % Instructions: Compute the cost of a particular choice of theta % You should set J to the cost. Z = (X * theta - y).^2; J = sum(Z(:,1)) / (2 * m); % ========================================================================= end
这里的(X * theta – y)得到一个列向量,用标量平方得到每个元素的平方,接着对其求和,取平均得到J。
梯度下降
% run gradient descent theta = gradientDescent(X, y, theta, alpha, iterations);
其实现如下:
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters) %GRADIENTDESCENT Performs gradient descent to learn theta % theta = GRADIENTDESENT(X, y, theta, alpha, num_iters) updates theta by % taking num_iters gradient steps with learning rate alpha % Initialize some useful values m = length(y); % number of training examples J_history = zeros(num_iters, 1); for iter = 1:num_iters % ====================== YOUR CODE HERE ====================== % Instructions: Perform a single gradient step on the parameter vector % theta. % % Hint: While debugging, it can be useful to print out the values % of the cost function (computeCost) and gradient here. % % z = (X * theta - y)' * X; % temp1 = alpha / m * sum(z(:,1)); % temp2 = alpha / m * sum(z(:,2)); % temp = [temp1; temp2]; % theta = theta - temp; z = X' * (X * theta - y); theta = theta - alpha / m * z; % ============================================================ % Save the cost J in every iteration J_history(iter) = computeCost(X, y, theta); end end
上文说的同时使用所有实例的意思是,利用上个迭代的参数将求和部分一次性算完,本次迭代更新的任何参数都不影响求和。
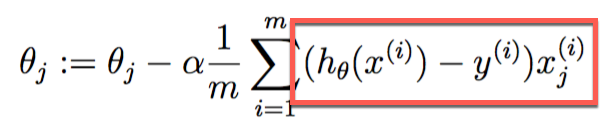
这里还保存了每个迭代的历史参数。细节上注意matlab索引从1开始,不是0。
可视化回归方程
% Plot the linear fit
hold on; % keep previous plot visible
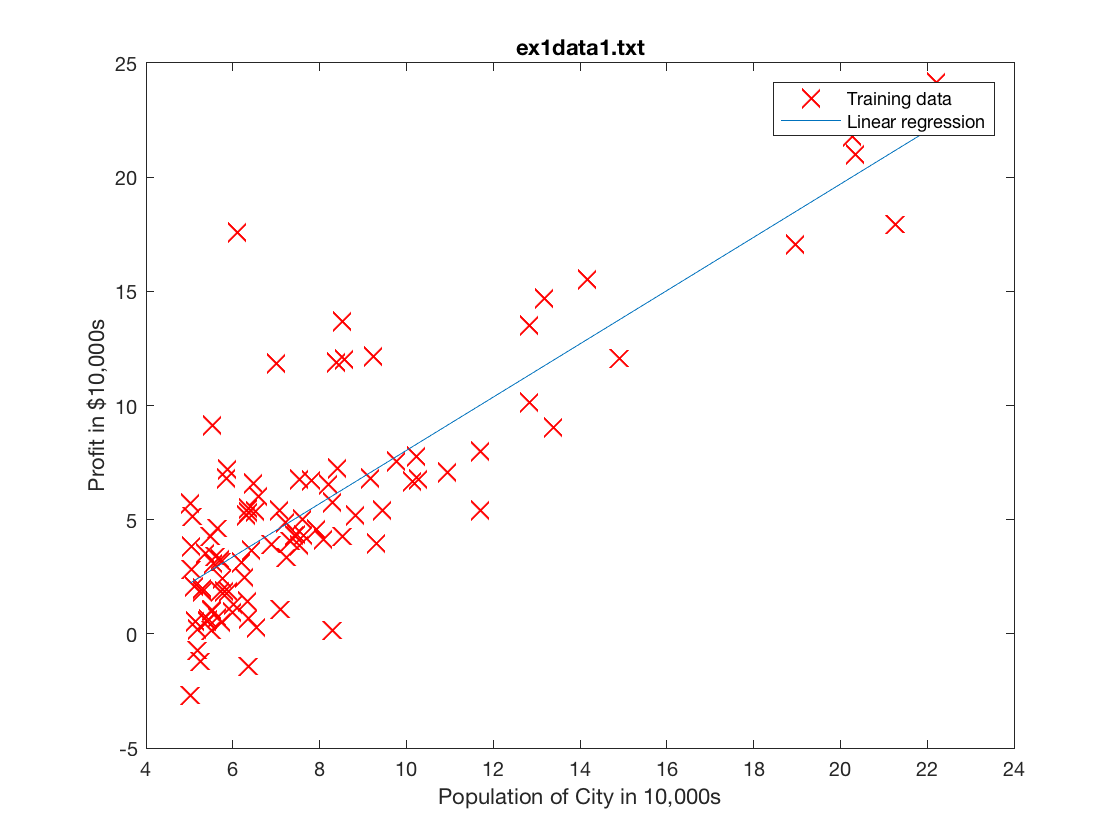
plot(X(:,2), X*theta, '-')
legend('Training data', 'Linear regression')
hold off % don't overlay any more plots on this figure
这里的hold on用得很好,如果没有关闭上一幅图的话,接下来的操作会在上一幅画的基础上进行。
可视化目标函数
利用matlab强大的绘图功能,以参数为xy轴,目标函数输出为z轴,直观展示目标函数长得什么样。
%% ============= Part 4: Visualizing J(theta_0, theta_1) =============
fprintf('Visualizing J(theta_0, theta_1) ...\n')
% Grid over which we will calculate J
theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);
% initialize J_vals to a matrix of 0's
J_vals = zeros(length(theta0_vals), length(theta1_vals));
% Fill out J_vals
for i = 1:length(theta0_vals)
for j = 1:length(theta1_vals)
t = [theta0_vals(i); theta1_vals(j)];
J_vals(i,j) = computeCost(X, y, t);
end
end
% Because of the way meshgrids work in the surf command, we need to
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals';
% Surface plot
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel('\theta_0'); ylabel('\theta_1');
surf函数接受x向量、y向量、z矩阵,画图:
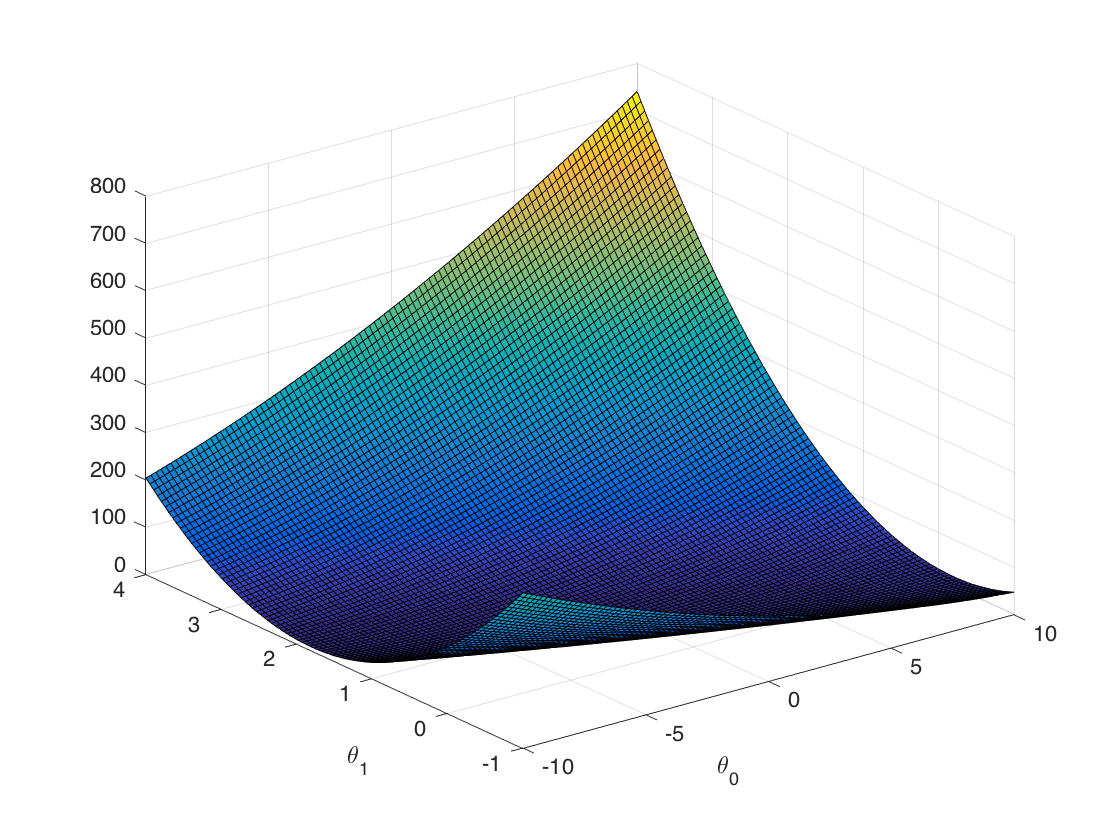
这是一个碗状的凸函数,其极值点位于碗底。用等高线图更直观:
% Contour plot
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel('\theta_0'); ylabel('\theta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);
contour函数前三个参数与surf一样,最后一个参数表示从z=0.01到z=100这两个平面之间,用20个平面去切割曲面,得到等高线:
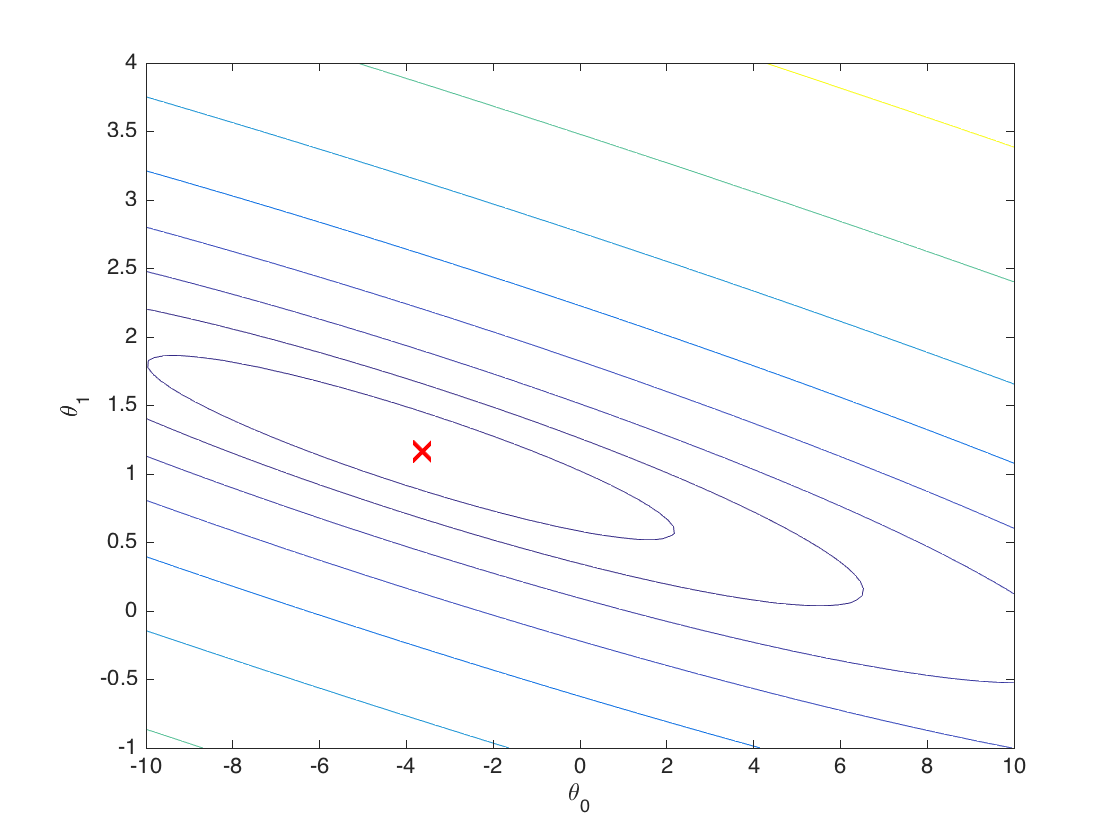
理解这幅图很简单,想象一下你正在俯视一个碗,碗的内壁有一圈圈的金丝线,就得到上图了。
多变量线性回归
这部分根据房子的面积和房间数预测房价。
数据可视化
老规矩,先看看数据长什么样:
%% Load Data
data = load('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);
stem3(data(:,1), data(:,2), data(:,3));
xlabel('size');
ylabel('number of bedrooms');
zlabel('price');
输出:
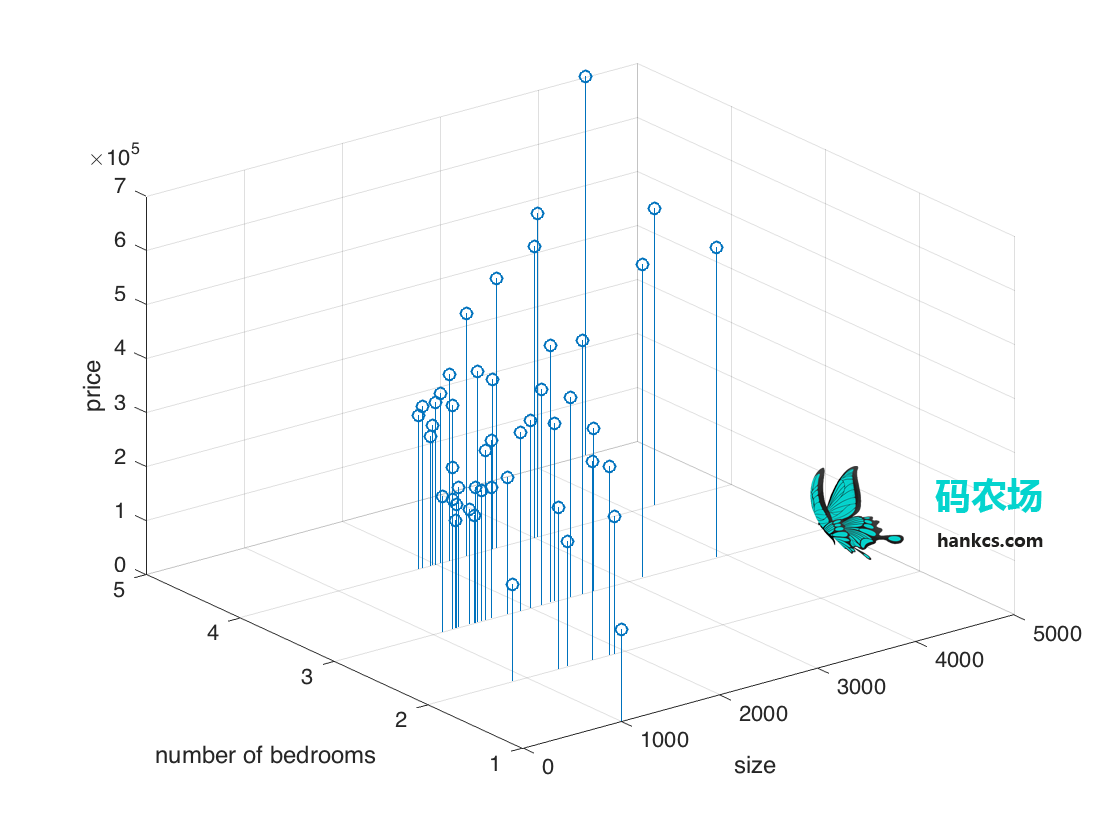
特征标准化
对于数值特征,将其标准化为均值=0,标准差=1。
function [X_norm, mu, sigma] = featureNormalize(X) %FEATURENORMALIZE Normalizes the features in X % FEATURENORMALIZE(X) returns a normalized version of X where % the mean value of each feature is 0 and the standard deviation % is 1. This is often a good preprocessing step to do when % working with learning algorithms. % You need to set these values correctly X_norm = X; mu = zeros(1, size(X, 2)); sigma = zeros(1, size(X, 2)); % ====================== YOUR CODE HERE ====================== % Instructions: First, for each feature dimension, compute the mean % of the feature and subtract it from the dataset, % storing the mean value in mu. Next, compute the % standard deviation of each feature and divide % each feature by it's standard deviation, storing % the standard deviation in sigma. % % Note that X is a matrix where each column is a % feature and each row is an example. You need % to perform the normalization separately for % each feature. % % Hint: You might find the 'mean' and 'std' functions useful. % features = size(X,2);%X????2?????? for i = 1 : features mu(i) = mean(X(:,i));%?? sigma(i) = std(X(:,i));%??? X_norm(:,i) = (X(:,i) - mu(i)) / sigma(i); end % ============================================================ end
标准化之后:
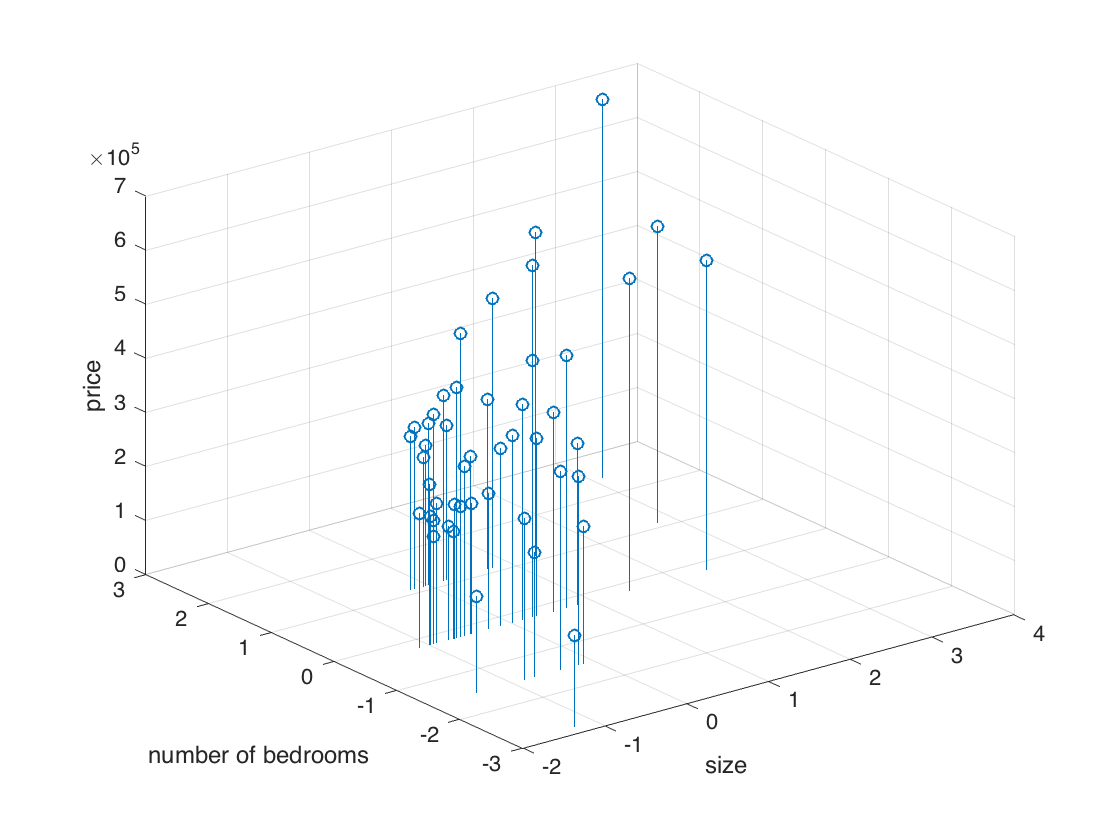
虽然直观上看不出来区别,但实际上坐标已经发生了线性的变化。
损失函数
向量版的J函数
![]()
其中
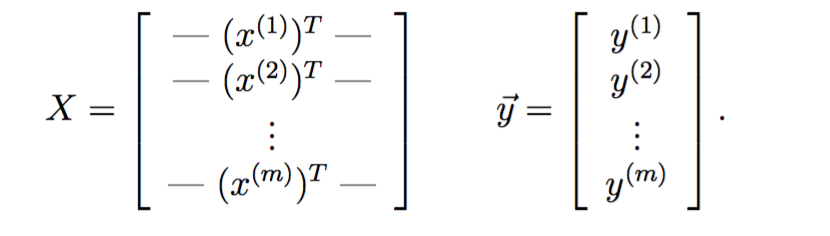
function J = computeCostMulti(X, y, theta) %COMPUTECOSTMULTI Compute cost for linear regression with multiple variables % J = COMPUTECOSTMULTI(X, y, theta) computes the cost of using theta as the % parameter for linear regression to fit the data points in X and y % Initialize some useful values m = length(y); % number of training examples % You need to return the following variables correctly J = 0; % ====================== YOUR CODE HERE ====================== % Instructions: Compute the cost of a particular choice of theta % You should set J to the cost. Z = (X * theta - y); J = Z' * Z / (2 * m); % ========================================================================= end
梯度下降
与单变量基本相同,只不过将computeCost换成多变量版本。
function [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters) %GRADIENTDESCENTMULTI Performs gradient descent to learn theta % theta = GRADIENTDESCENTMULTI(x, y, theta, alpha, num_iters) updates theta by % taking num_iters gradient steps with learning rate alpha % Initialize some useful values m = length(y); % number of training examples J_history = zeros(num_iters, 1); for iter = 1:num_iters % ====================== YOUR CODE HERE ====================== % Instructions: Perform a single gradient step on the parameter vector % theta. % % Hint: While debugging, it can be useful to print out the values % of the cost function (computeCostMulti) and gradient here. % z = X' * (X * theta - y); theta = theta - alpha / m * z; % ============================================================ % Save the cost J in every iteration J_history(iter) = computeCostMulti(X, y, theta); end end
跑了一个平面出来,画到原图上去:

录一个动画玩玩:
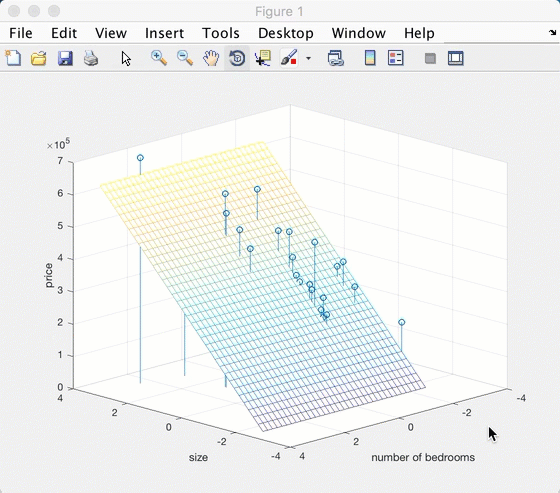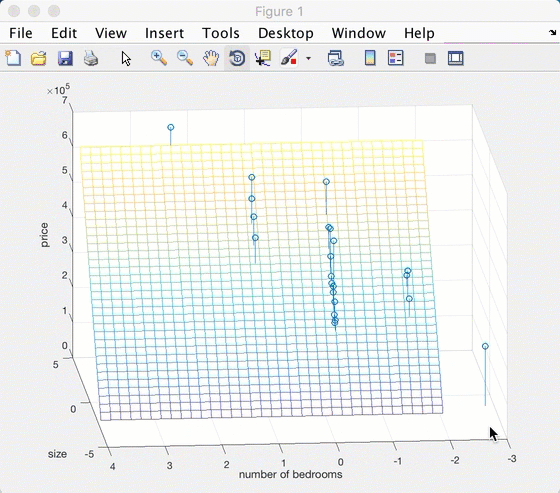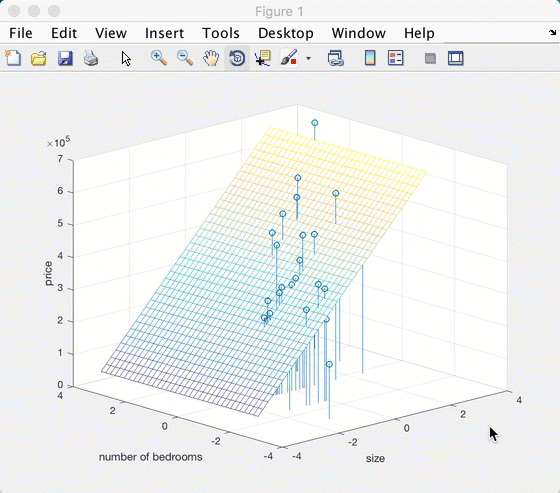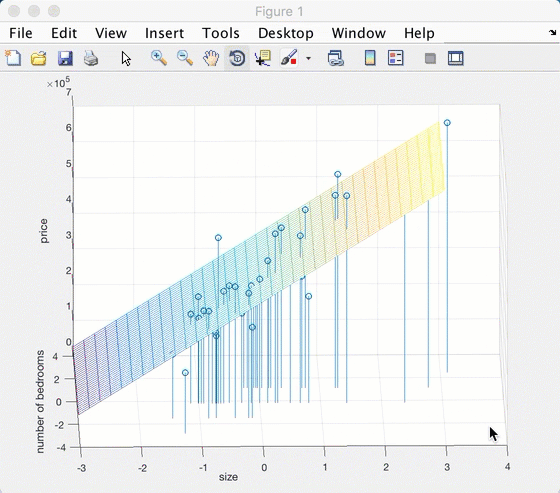
matlab还是很酷炫的嘛。
算法收敛速度:
% Plot the convergence graph
figure;
plot(1:numel(J_history), J_history, '-b', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J');
输出:
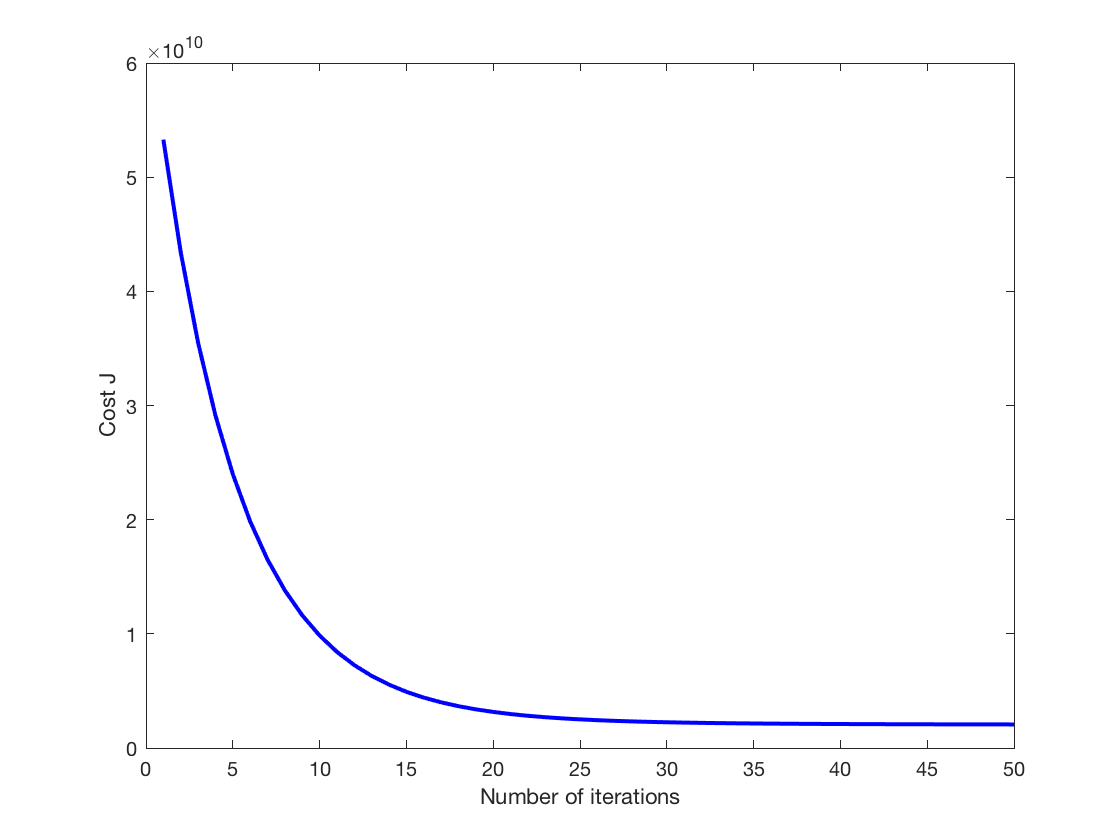
这里由于有3个参数,加上J等于4维,所以无法像单变量那样可视化了。
正规方程法
事实上,可以不用任何数值方法,直接用解析法得出最优参数:
![]()
很简单的矩阵运算:
function [theta] = normalEqn(X, y) %NORMALEQN Computes the closed-form solution to linear regression % NORMALEQN(X,y) computes the closed-form solution to linear % regression using the normal equations. % ====================== YOUR CODE HERE ====================== % Instructions: Complete the code to compute the closed form solution % to linear regression and put the result in theta. % % ---------------------- Sample Solution ---------------------- theta = inv(X' * X) * X' * y; % ------------------------------------------------------------- % ============================================================ end
 码农场
码农场
你好,可以提供一下作业里面的txt文件吗??急需,到处都找不到
老大咋不玩玩R
暂时还没碰到这个需求