CS229编程2：逻辑斯谛回归

斯坦福cs229 MATLAB公开课，简称ML公开课。这是第二次编程练习，本次重点是无约束非线性规划函数fminunc的用法，以及一些作图的技巧。

简介 

实现逻辑斯谛回归，并应用到给定的两个数据集上。

逻辑斯谛回归 

根据两门考试的成绩预测学生是否能够录取：

34.62365962451697,78.0246928153624,0
30.28671076822607,43.89499752400101,0
35.84740876993872,72.90219802708364,0
60.18259938620976,86.30855209546826,1
79.0327360507101,75.3443764369103,1

加载：

%% Load Data
%  The first two columns contains the exam scores and the third column
%  contains the label.
 
data = load('ex2data1.txt');
X = data(:, [1, 2]); y = data(:, 3);

可视化数据

%% ==================== Part 1: Plotting ====================
%  We start the exercise by first plotting the data to understand the 
%  the problem we are working with.
 
fprintf(['Plotting data with + indicating (y = 1) examples and o ' ...
         'indicating (y = 0) examples.\n']);
 
plotData(X, y);
 
% Put some labels 
hold on;
% Labels and Legend
xlabel('Exam 1 score')
ylabel('Exam 2 score')
 
% Specified in plot order
legend('Admitted', 'Not admitted')
hold off;

matlab中的…就是个连接符，有些行太长了，用…分割一下。

plotData具体实现：

function plotData(X, y)
%PLOTDATA Plots the data points X and y into a new figure 
%   PLOTDATA(x,y) plots the data points with + for the positive examples
%   and o for the negative examples. X is assumed to be a Mx2 matrix.
 
% Create New Figure
figure; hold on;
 
% ====================== YOUR CODE HERE ======================
% Instructions: Plot the positive and negative examples on a
%               2D plot, using the option 'k+' for the positive
%               examples and 'ko' for the negative examples.
%
% Find Indices of Positive and Negative Examples
pos = find(y==1); neg = find(y == 0);
% Plot Examples
plot(X(pos, 1), X(pos, 2), 'k+','LineWidth', 2, ...
'MarkerSize', 7);
plot(X(neg, 1), X(neg, 2), 'ko', 'MarkerFaceColor', 'y', ...
'MarkerSize', 7);

find函数返回满足条件的下标，plot一共两次，与legend两次对应。

legend制作图例

legend('string1','string2',...,pos)		

不传位置参数表示自动寻找合适位置放置图例：

得到：

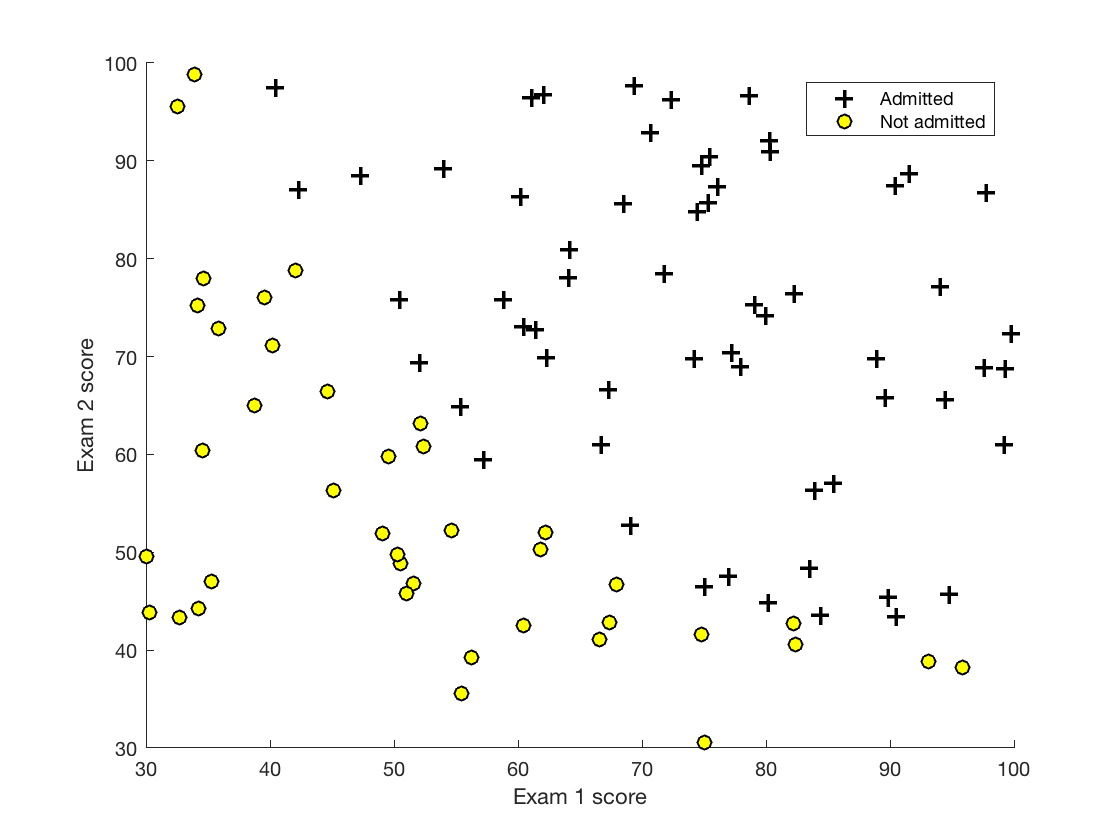
可以直观地看出数据大致是线性可分的，可以预计逻辑斯谛回归模型适用于该数据。

实现sigmoid函数

逻辑斯谛回归模型的假设函数为：

其中g为sigmoid函数：

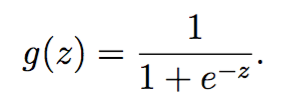
实现如下：

function g = sigmoid(z)
%SIGMOID Compute sigmoid functoon
%   J = SIGMOID(z) computes the sigmoid of z.
 
% You need to return the following variables correctly 
g = zeros(size(z));
 
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the sigmoid of each value of z (z can be a matrix,
%               vector or scalar).
 
g = 1 ./ (1 + exp(-z));
 
 
 
% =============================================================
 
end

注意./为element-wise除法。

损失函数和梯度

损失函数为假设函数h在整个训练集上的对数似然函数的相反数：

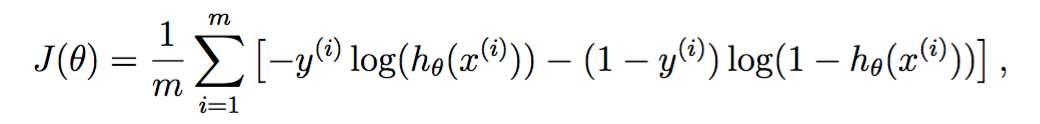
其导数为

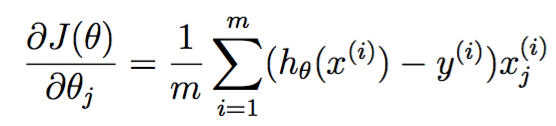
被实现为costFunction，这个名字取得不太好，明明干了两件事情的：

function [J, grad] = costFunction(theta, X, y)
%COSTFUNCTION Compute cost and gradient for logistic regression
%   J = COSTFUNCTION(theta, X, y) computes the cost of using theta as the
%   parameter for logistic regression and the gradient of the cost
%   w.r.t. to the parameters.
 
% Initialize some useful values
m = length(y); % number of training examples
 
% You need to return the following variables correctly 
J = 0;
grad = zeros(size(theta));
 
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
%               You should set J to the cost.
%               Compute the partial derivatives and set grad to the partial
%               derivatives of the cost w.r.t. each parameter in theta
%
% Note: grad should have the same dimensions as theta
%
 
 
J = 1 / m * [- y' * log(sigmoid(X * theta)) - (1 - y') * log(1 - sigmoid(X * theta))];
 
grad = 1 / m * X' * (sigmoid(X * theta) - y);
 
 
 
% =============================================================
 
end

得到损失函数J的值——一个标量，和梯度向量。

调用方法如下：

%% ============ Part 2: Compute Cost and Gradient ============
%  In this part of the exercise, you will implement the cost and gradient
%  for logistic regression. You neeed to complete the code in 
%  costFunction.m
 
%  Setup the data matrix appropriately, and add ones for the intercept term
[m, n] = size(X);
 
% Add intercept term to x and X_test
X = [ones(m, 1) X];
 
% Initialize fitting parameters
initial_theta = zeros(n + 1, 1);
 
% Compute and display initial cost and gradient
[cost, grad] = costFunction(initial_theta, X, y);
 
fprintf('Cost at initial theta (zeros): %f\n', cost);
fprintf('Gradient at initial theta (zeros): \n');
fprintf(' %f \n', grad);
 
fprintf('\nProgram paused. Press enter to continue.\n');
pause;

学习参数

用到了无约束非线性规划函数优化方法fminunc，基本用法是：

更多信息详见附录。

调用方法

%% ============= Part 3: Optimizing using fminunc  =============
%  In this exercise, you will use a built-in function (fminunc) to find the
%  optimal parameters theta.
 
%  Set options for fminunc
options = optimset('GradObj', 'on', 'MaxIter', 400);
 
%  Run fminunc to obtain the optimal theta
%  This function will return theta and the cost 
[theta, cost] = ...
    fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);
 
% Print theta to screen
fprintf('Cost at theta found by fminunc: %f\n', cost);
fprintf('theta: \n');
fprintf(' %f \n', theta);
 
% Plot Boundary
plotDecisionBoundary(theta, X, y);
 
% Put some labels 
hold on;
% Labels and Legend
xlabel('Exam 1 score')
ylabel('Exam 2 score')
 
% Specified in plot order
legend('Admitted', 'Not admitted')
hold off;
 
fprintf('\nProgram paused. Press enter to continue.\n');
pause;

这里还有个绘制决策边界的函数：

function plotDecisionBoundary(theta, X, y)
%PLOTDECISIONBOUNDARY Plots the data points X and y into a new figure with
%the decision boundary defined by theta
%   PLOTDECISIONBOUNDARY(theta, X,y) plots the data points with + for the 
%   positive examples and o for the negative examples. X is assumed to be 
%   a either 
%   1) Mx3 matrix, where the first column is an all-ones column for the 
%      intercept.
%   2) MxN, N>3 matrix, where the first column is all-ones
 
% Plot Data
plotData(X(:,2:3), y);
hold on
 
if size(X, 2) <= 3
    % Only need 2 points to define a line, so choose two endpoints
    plot_x = [min(X(:,2))-2,  max(X(:,2))+2];
 
    % Calculate the decision boundary line
    plot_y = (-1./theta(3)).*(theta(2).*plot_x + theta(1));
 
    % Plot, and adjust axes for better viewing
    plot(plot_x, plot_y)
    
    % Legend, specific for the exercise
    legend('Admitted', 'Not admitted', 'Decision Boundary')
    axis([30, 100, 30, 100])
else
    % Here is the grid range
    u = linspace(-1, 1.5, 50);
    v = linspace(-1, 1.5, 50);
 
    z = zeros(length(u), length(v));
    % Evaluate z = theta*x over the grid
    for i = 1:length(u)
        for j = 1:length(v)
            z(i,j) = mapFeature(u(i), v(j))*theta;
        end
    end
    z = z'; % important to transpose z before calling contour
 
    % Plot z = 0
    % Notice you need to specify the range [0, 0]
    contour(u, v, z, [0, 0], 'LineWidth', 2)
end
hold off
 
end

如果数据特征维度小于等于2的话（代码中是3，因为第一列实际上都是1，是为了bias准备的），直接画到平面上去，取两点plot直线。

预测与评估

有了参数，给定输入，传进假设函数，得到几率，根据几率是否大于0.5做出预测。

function p = predict(theta, X)
%PREDICT Predict whether the label is 0 or 1 using learned logistic 
%regression parameters theta
%   p = PREDICT(theta, X) computes the predictions for X using a 
%   threshold at 0.5 (i.e., if sigmoid(theta'*x) >= 0.5, predict 1)
 
m = size(X, 1); % Number of training examples
 
% You need to return the following variables correctly
p = zeros(m, 1);
 
% ====================== YOUR CODE HERE ======================
% Instructions: Complete the following code to make predictions using
%               your learned logistic regression parameters. 
%               You should set p to a vector of 0's and 1's
%
prob = sigmoid(X * theta);
for i = 1 : m
    if prob(i) >= 0.5
        p(i) = 1;
    else
        p(i) = 0;
    end
end
 
 
 
 
 
 
 
% =========================================================================
 
 
end

有了预测函数，可以在训练集上跑一下评估：

%% ============== Part 4: Predict and Accuracies ==============
%  After learning the parameters, you'll like to use it to predict the outcomes
%  on unseen data. In this part, you will use the logistic regression model
%  to predict the probability that a student with score 45 on exam 1 and 
%  score 85 on exam 2 will be admitted.
%
%  Furthermore, you will compute the training and test set accuracies of 
%  our model.
%
%  Your task is to complete the code in predict.m
 
%  Predict probability for a student with score 45 on exam 1 
%  and score 85 on exam 2 
 
prob = sigmoid([1 45 85] * theta);
fprintf(['For a student with scores 45 and 85, we predict an admission ' ...
         'probability of %f\n\n'], prob);
 
% Compute accuracy on our training set
p = predict(theta, X);
 
fprintf('Train Accuracy: %f\n', mean(double(p == y)) * 100);
 
fprintf('\nProgram paused. Press enter to continue.\n');
pause;

p == y得到布尔向量，转为双精度求均值得到accuracy。

正则化逻辑斯谛回归

这部分利用正则化逻辑斯谛回归，根据某芯片的两个参数预测其是否合格。

0.051267,0.69956,1
-0.092742,0.68494,1
-0.21371,0.69225,1
-0.375,0.50219,1
-0.51325,0.46564,1

数据可视化

%% Load Data
%  The first two columns contains the X values and the third column
%  contains the label (y).
 
data = load('ex2data2.txt');
X = data(:, [1, 2]); y = data(:, 3);
 
plotData(X, y);
 
% Put some labels 
hold on;
 
% Labels and Legend
xlabel('Microchip Test 1')
ylabel('Microchip Test 2')
 
% Specified in plot order
legend('y = 1', 'y = 0')
hold off;

代码跟上一章一模一样，得到：

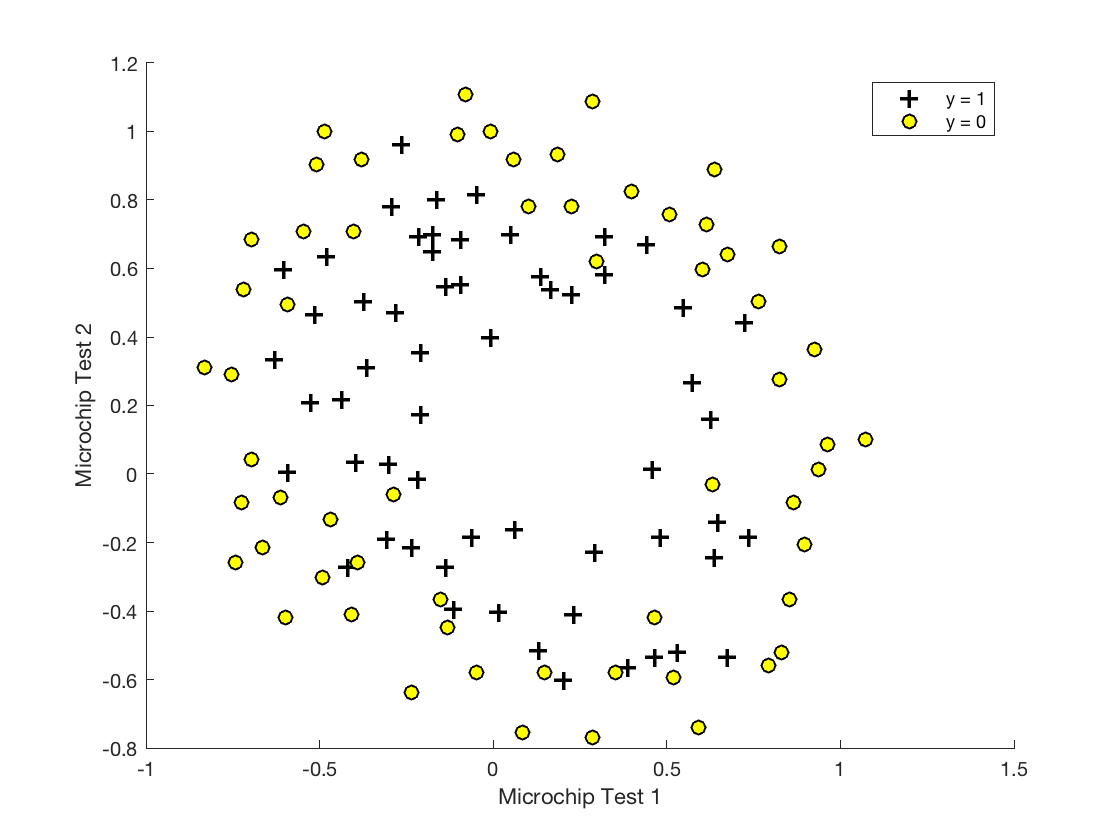
这次的数据明显不是线性可分的，尝试加入更多特征。特征越多，线性可分的可能性越高。没有额外特征？那就把已有特征取个n次方映射为新特征，创造条件也要上。

如果最高六次方的话，则为：

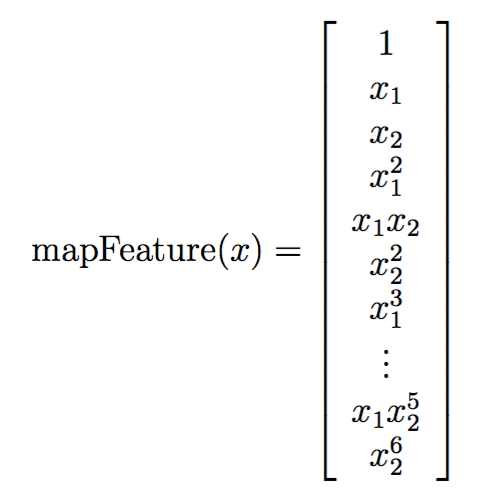
其实现如下：

function out = mapFeature(X1, X2)
% MAPFEATURE Feature mapping function to polynomial features
%
%   MAPFEATURE(X1, X2) maps the two input features
%   to quadratic features used in the regularization exercise.
%
%   Returns a new feature array with more features, comprising of 
%   X1, X2, X1.^2, X2.^2, X1*X2, X1*X2.^2, etc..
%
%   Inputs X1, X2 must be the same size
%
 
degree = 6;
out = ones(size(X1(:,1)));
for i = 1:degree
    for j = 0:i
        out(:, end+1) = (X1.^(i-j)).*(X2.^j);
    end
end
 
end

下标中的end用法如下：

这边被用作了append操作。

损失函数和梯度

损失函数多了个L2正则化项：

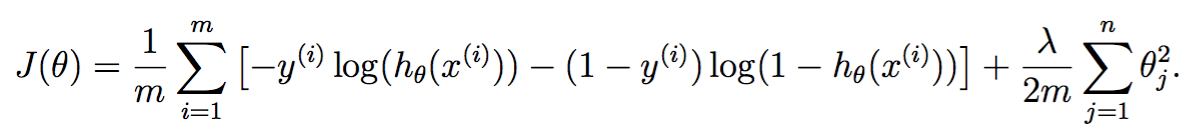
作为bias的不应参与正则化项，所以上式j从1开始，matlab中下标从2开始。

梯度如下：

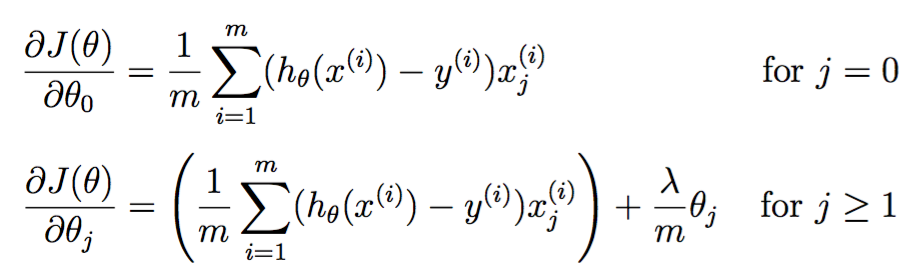
实现如下：

function [J, grad] = costFunctionReg(theta, X, y, lambda)
%COSTFUNCTIONREG Compute cost and gradient for logistic regression with regularization
%   J = COSTFUNCTIONREG(theta, X, y, lambda) computes the cost of using
%   theta as the parameter for regularized logistic regression and the
%   gradient of the cost w.r.t. to the parameters. 
 
% Initialize some useful values
m = length(y); % number of training examples
 
% You need to return the following variables correctly 
J = 0;
grad = zeros(size(theta));
 
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
%               You should set J to the cost.
%               Compute the partial derivatives and set grad to the partial
%               derivatives of the cost w.r.t. each parameter in theta
 
 
J = 1 / m * [- y' * log(sigmoid(X * theta)) ...
    - (1 - y') * log(1 - sigmoid(X * theta))] ...
    + lambda / 2 / m * (theta' * theta - theta(1) * theta(1));
 
grad = 1 / m * X' * (sigmoid(X * theta) - y) ...
    + lambda / m * theta;
grad(1) = grad(1) - lambda / m * theta(1);
 
 
 
 
% =============================================================
 
end

在这份实现中，先忽略的特殊性，一股脑地算出来，然后将的梯度额外减去正则化项。

学习参数

无约束最小化，跟上一章一摸一样：

%% ============= Part 2: Regularization and Accuracies =============
%  Optional Exercise:
%  In this part, you will get to try different values of lambda and 
%  see how regularization affects the decision coundart
%
%  Try the following values of lambda (0, 1, 10, 100).
%
%  How does the decision boundary change when you vary lambda? How does
%  the training set accuracy vary?
%
 
% Initialize fitting parameters
initial_theta = zeros(size(X, 2), 1);
 
% Set regularization parameter lambda to 1 (you should vary this)
lambda = 1;
 
% Set Options
options = optimset('GradObj', 'on', 'MaxIter', 400);
 
% Optimize
[theta, J, exit_flag] = ...
    fminunc(@(t)(costFunctionReg(t, X, y, lambda)), initial_theta, options);
 
% Plot Boundary
plotDecisionBoundary(theta, X, y);
hold on;
title(sprintf('lambda = %g', lambda))
 
% Labels and Legend
xlabel('Microchip Test 1')
ylabel('Microchip Test 2')
 
legend('y = 1', 'y = 0', 'Decision boundary')
hold off;
 
% Compute accuracy on our training set
p = predict(theta, X);
 
fprintf('Train Accuracy: %f\n', mean(double(p == y)) * 100);

可视化决策边界

函数还是那个函数，只不过进入了第二个分支：

    % Here is the grid range
    u = linspace(-1, 1.5, 50);
    v = linspace(-1, 1.5, 50);
 
    z = zeros(length(u), length(v));
    % Evaluate z = theta*x over the grid
    for i = 1:length(u)
        for j = 1:length(v)
            z(i,j) = mapFeature(u(i), v(j))*theta;
        end
    end
    z = z'; % important to transpose z before calling contour
 
    % Plot z = 0
    % Notice you need to specify the range [0, 0]
    contour(u, v, z, [0, 0], 'LineWidth', 2)

这个作图很精妙，决策边界位于中的等于0的时候，此时几率为0.5，是决策的临界点。所以先把一个区域内所有点的都算出来，但最后只画==0的那些，也就是用contour的[0, 0]参数来约束。

我发现v向量最低长度得为2，不然就会被当做标量0处理，退化为：

结果一条线也看不到。

运行后得到图形：

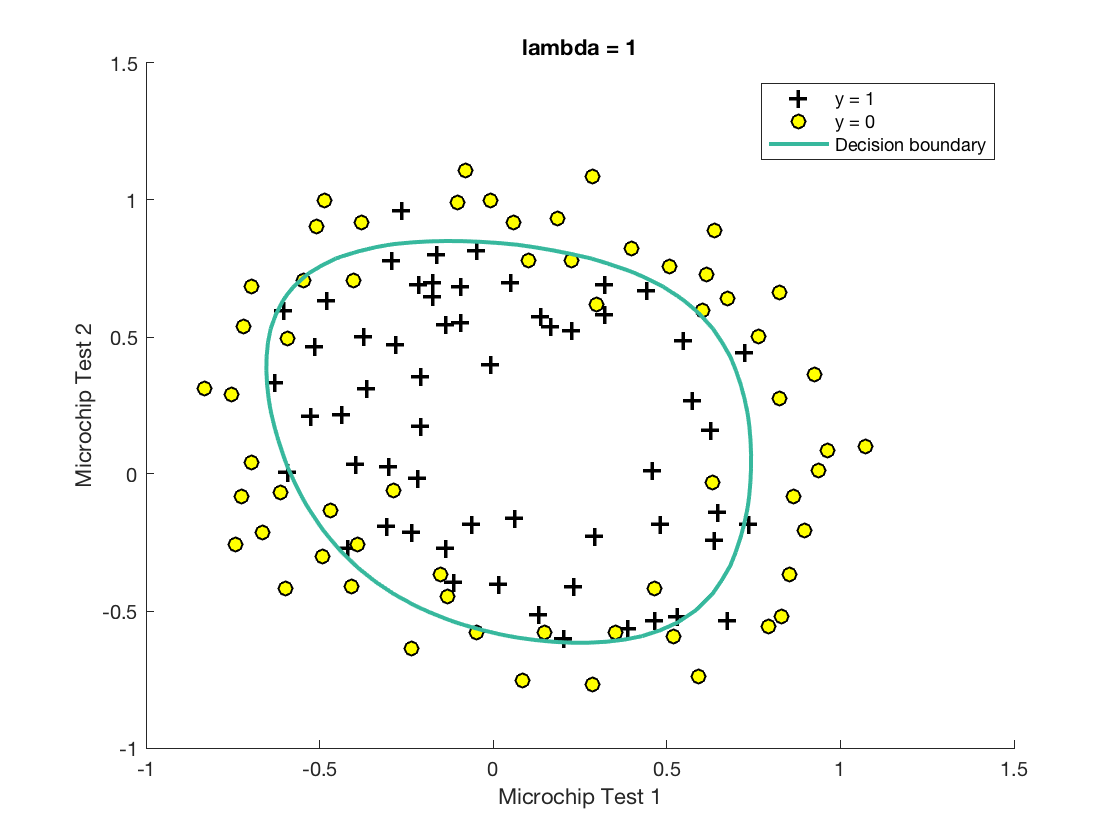
通过修改λ的值，可以得到欠拟合和过拟合的图例：

欠拟合：

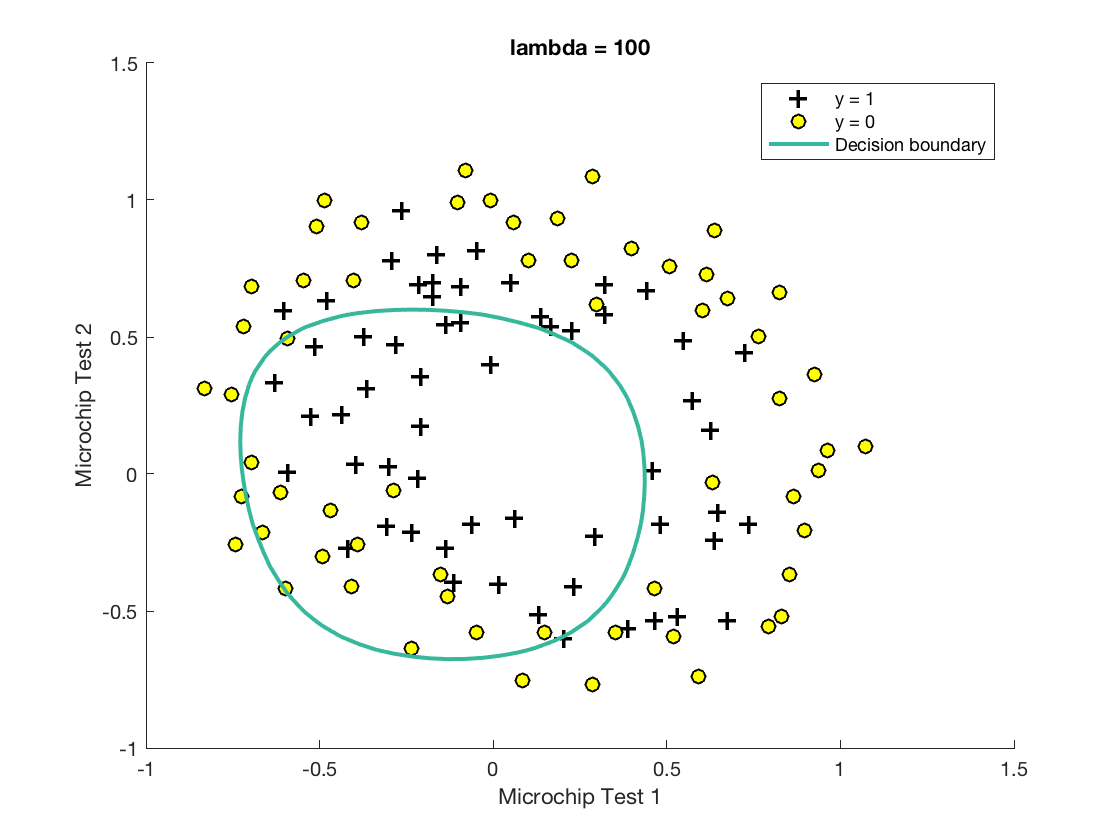
过拟合：

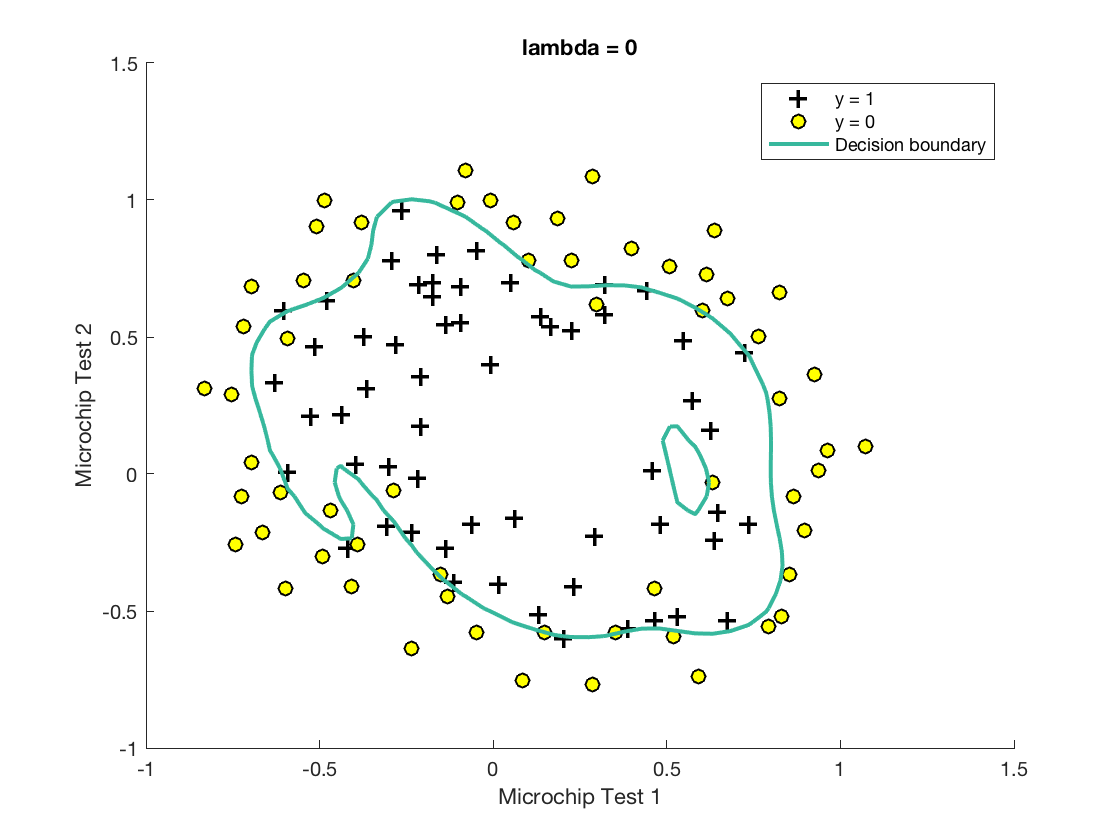
附录

 知识共享署名-非商业性使用-相同方式共享：码农场 » CS229编程2：逻辑斯谛回归