目录
多层神经网络常见问题
如果初始学习率特别大,则每个隐藏单元的权值的绝对值就会变得很大。此时它们的状态就不再取决于输入(可能是因为bias那么大)。不取决于输入也就是说它们的误差导数会变得很小,接近零的导数说明它们位于一个高原上,而很多人会误以为此时达到了局部最优点,就急匆匆地终止了训练。
另一个问题是,分类任务中,如果用squared error或cross entropy error作为损失函数,输出单元会倾向于做如下不痛不痒的猜测:总是输出训练数据中标签=1的频率(即一直在学习截距,而没有在学习weight)。如果学习率过小,则需要很长一段时间让神经网络学习到有用的weight。从结果上来看,error一开始下降很快(bias学习期),之后很长一段时间都没有多少改变(weight学习期),也会让人误以为达到了局部最优。
过早减小学习率的危害
较小的学习率可以减少不同mini-batch之间随机的error波动,所以有立竿见影的效果。但之后的学习会变慢。
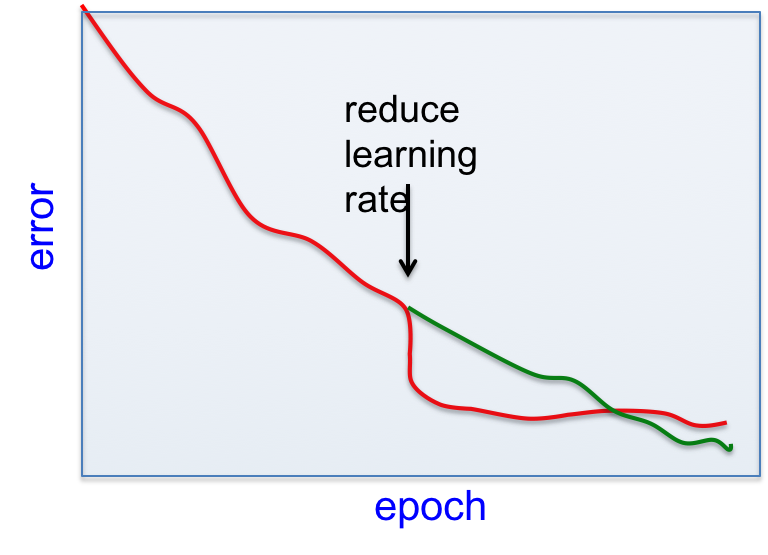
加快mini-batch训练的4种方法
1. 使用“动量”(通俗地讲,就是一种梯度上的“惯性”,或说“平滑算法”)。
$$\begin{align}v &= \gamma v+ \alpha \nabla_{\theta} J(\theta; x^{(i)},y^{(i)}) \\\theta &= \theta - v\end{align}$$
2. 对不同参数使用不同的学习率,如果梯度的符号经常变化,则减小学习率,否则增大。
3. rmsprop:对某个参数的梯度,将其学习率除以历史值的平均。(这样做了之后,权值的更新矢量的每个维度上的标量值的绝对值近似为1,相当于只利用梯度的符号;这是类似full-batch中的R prompt的mini-batch版)
4. 从最优化理论中借鉴使用曲率信息调整学习率(不会讲)。
动量法
直观理解
想象error surface上的一个小球,小球的坐标中除去error剩下的维度代表当前的权值向量。用当前梯度的外力将小球推出去(其实可以理解为小球原来是抓在手上的,现在松手,在重力的作用下小球开始滚动),一旦小球有了速度,它就不会按照当前的梯度运行。这是因为它有惯性,在动量的作用下,它会倾向于维持原来的方向,而不是绝对按照当前曲面的梯度走。
我们的目标是让小球尽快到达碗底,也就是尽快损失重力势能。动量的作用是减小高曲率方向上的震荡,如下图所示:
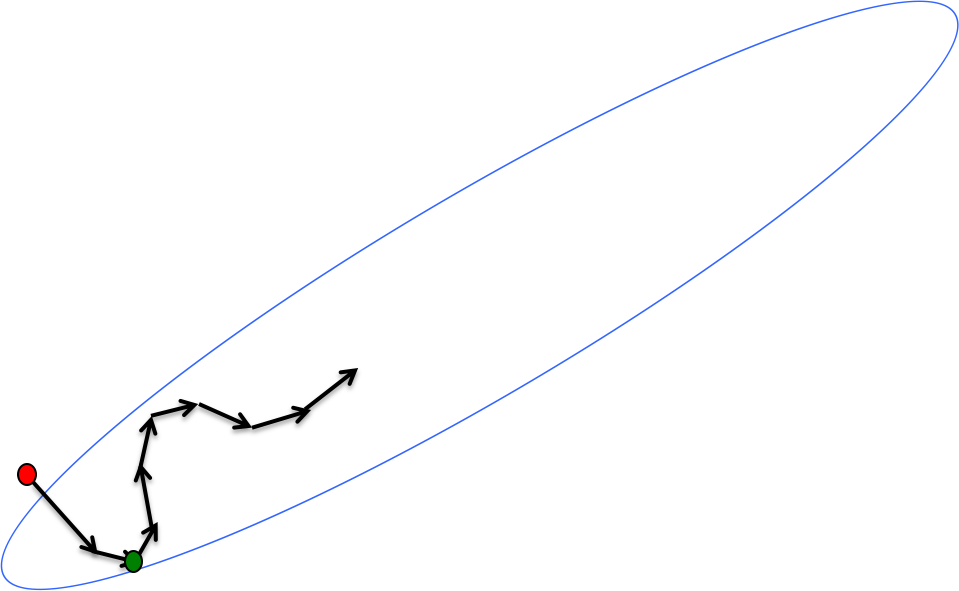
红点与绿点的梯度几乎完全相反,如果没有惯性(动量)的话,小球会近似在两点间震荡多次。有了动量,垂直于山谷的速度被抵消掉;而沿着山谷下降的速度则得到了保留。而且下降的速度越积越多,当动量稳定的时候,你就会得到一个很快的下降速度。
公式
动量更新法的公式十分简单:
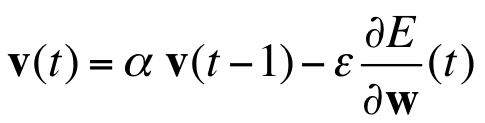
括号中的t代表迭代时刻,$alpha$动量因子控制惯性的大小(有点像质量与外力的比值,通常取略小于1的值),后面再加上当前梯度(外力)的影响,得到当前速度,作为权值的更新量。
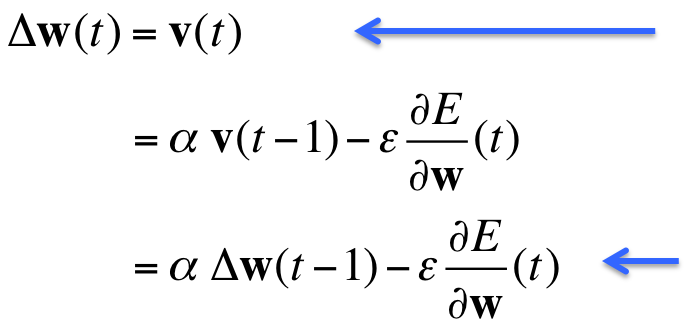
如果error surface是一个倾斜面($\frac{\partial E}{\partial W}(t)$是常量)的话,最终速度会趋近于如下常量:
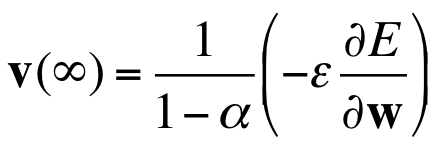
从这个式子可以看出如果$alpha$接近1的话,速度将会非常大。
另外这也启发我们,如果初始$alpha$特别接近1的话,那么初始更新量也会特别特别大。所以初始动量应该小一点(0.5)。一旦梯度不是那么大了,说明权值小球在峡谷里动弹不得的时候,就可以渐进地增加到0.9甚至0.99。
有了动量因子去“防震荡”,我们就可以大胆地使用大一点的学习率。
优化的动量法
标准的动量法是先计算当前位置的梯度,然后在累计的方向上前进一大步。Ilya Sutskever 在2012年提出了一种优化版本:先在历史累计方向上前进一大步,然后在新位置上计算梯度并修正方向。可以这么理解,最好犯错之后去改正它。
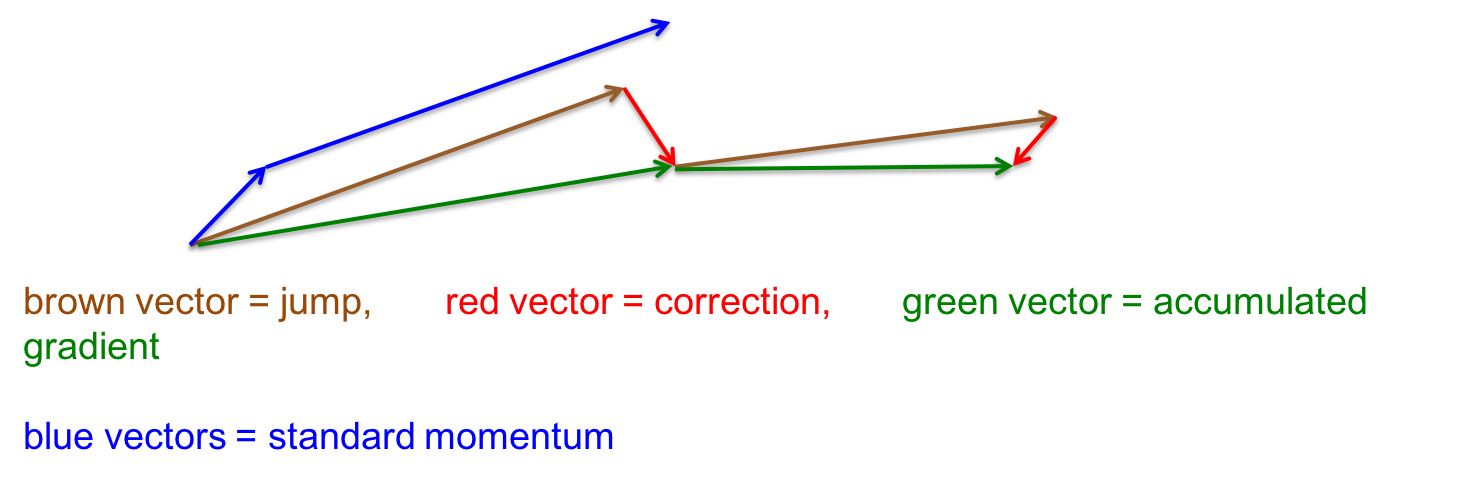
在上面这张示意图中,蓝色是标准版的动量法,先在当前的梯度方向上裹足不前,然后突然在历史方向上前进一大步。棕色和红色是改进的动量法,恰好反过来(上图中前后有两次改进动量法,绿色分别是最终效果)。
每个连接的独立自适应学习率
让每个连接都拥有自己的学习率,根据经验随机应变。
直观理解
在多层神经网络中,不同的权值的最佳学习率各不相同,因为
-
梯度数量级相差巨大,特别是当初始权值较小的时候。
-
一个单元的入度决定了同时改变所有输入的权值所带来的效果大小
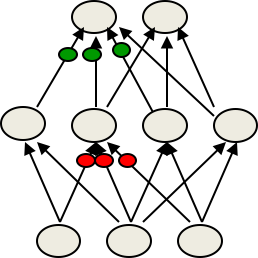
试想如果红点特别多的话,那么每个点改变一点点,累积的改变量就很大了,很容易过量。
所以一般采用这样的办法,有一个全局学习率,然后根据每个权值适当调整。
一种独立学习率的确定方法
具体怎么调整呢,有种方法是这样的:
-
初始化局部gain $g_{ij}=1$ ,与学习率一起确定最终更新量:
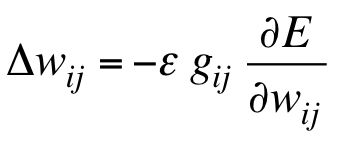
-
如果下次该权值的梯度符号不变则增加它的gain,否则减小
-
具体操作的时候,增加用加法,减小用乘法:
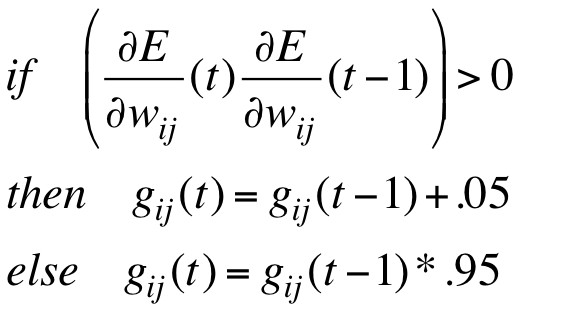
指数减小保证了大gain会在震荡开始的时候迅速衰减下去。一个有趣的现象是,如果梯度是完全随机的话,gain会大致为1(体会不到哪里有趣了)。如果梯度反复震荡,更新量会减小得很快;反之在顺流而下的时候,更新量会缓慢增加。
小技巧
-
将gain限制在某个合理的范围,比如[0.1, 10] 或 [.01, 100]。
-
使用full-batch或很大的mini-batch,毕竟这样保证了梯度的符号不易受mini-batch的采样误差影响。
-
综合adaptive learning和动量更新法,以当前梯度和当前速度的符号来上面的if-else决策。
rmsprop:将梯度除以历史数量级
全局学习率之所以难选,主要是因为每个权值的数量级相差巨大。在full batch中,可以利用梯度的符号来替代其本身,从而解决这个问题。
-
这样所有权值更新量的数量级都是相同的
-
这样可以快速脱离梯度极小的高原(管你梯度多小,我总是正负单位1)
-
我们不能通过增大学习率来实现这个效果,因为在梯度极大的时候,更新量会过大。
rprop结合了“只用符号”和“专享学习率”的思想。
-
它不检查权值的数量级,只使用符号
-
如果连续两次符号相等,则将局部学习率乘以比如1.2这样的值
-
否则乘以0.5这样的值
-
将局部学习率控制在百万分之一到五十之间
rprop为什么不适用于mini-batch
上面一直在说用于full-batch或很大的mini-batch,那为什么不能用于mini-batch呢?
因为这违反了SGD的中心思想。
SGD的中心思想是当学习率很小的时候,权值更新量其实是当前mini-batch的梯度和历史梯度的平均。举例来讲,假设某个权值在9个批次中的梯度是+0.1,在第10个批次中的梯度是-0.9,我们希望这个权值大致不变。
rprop会以绝对值相同的delta执行9次加法和1次减法(假定局部学习率的改变不显著),所以权值会增加不少。
是否存在一种方法可以同时具备:
-
rprop的稳定性
-
mini-batch的高效性
-
mini-batch间的有效平均
rmsprop
有。
-
rprop等效于使用梯度,只不过将其除以自身的绝对值。将其用于mini-batch的不合适之处是,每个mini-batch都除以了不同的值(导致不好平均)。所以为什么不强制相邻批次之间的分母为一个近似固定的值呢?
-
rmsprop:思路就是维护一个历史梯度的平方均值:
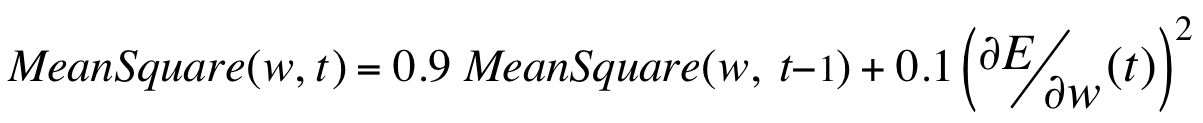
-
将梯度除以平方均值的开方
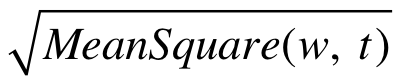 会促进学习效果。
会促进学习效果。
rmsprop的深入研究
标准动量更新效果不好,需要再研究。
改进的动量法中,如果将correction而不是历史梯度除以上述开方值,会得到最佳疗效。
结合adaptive learning rate也是需要再研究。
还有很多工作都在研究rmsprop。
神经网络的训练方法总结
-
对小数据集(10000以内)或者没有多少重复数据的大数据集,应当使用full-batch的一些优化方法,如Conjugate gradient、 LBFGS(老爷子说,有很多现成的package可以直接拿来用,写paper的时候直接说我用了什么什么方法这就是结果就行了,不需要探讨为什么要这么做,最省事了)。然后试试adaptive learning rates, rprop ...,它们是为神经网络而设计的方法。
-
对含有重复数据的大数据集,应当使用mini-batch。尝试动量法SGD,rmsprop 或LeCun的最新研究成果
你可能会问为什么有这么多麻烦事,为什么没有一个万金油的解决方案呢?
因为神经网络各不相同:
-
非常深的神经网络(特别是最后的几层节点数特别少的时候),到后面梯度会变得很小。
-
Recurrent神经网络很难记住很久之前的事件。
-
浅而宽的神经网络(实践中经常用,不需要很准确的学习方法,反正中心思想是要在过拟合之前结束训练,早点结束也没什么大不了的)
任务不同
-
一些任务需要精准的权值,另一些不需要
-
NLP中经常出现稀有词,而图像处理中没多少“稀有像素”
总之有许多训练神经网络的trick,需要根据具体情况去做实验才能确定。
![]() 知识共享署名-非商业性使用-相同方式共享:码农场 » Hinton神经网络公开课6 Optimization: How to make the learning go faster
知识共享署名-非商业性使用-相同方式共享:码农场 » Hinton神经网络公开课6 Optimization: How to make the learning go faster
 码农场
码农场