随机梯度下降与卷积神经网络

斯坦福UFLDL中CNN剩下两章的笔记，辅以两次编程练习，至此完成了CNN的学习。

梯度下降概述

诸如L-BFGS之类的批优化方法每次更新都使用整个训练集，能够收敛到局部最优。因为要设置的超参数很少，所以很好用，matlab里也有许多类似minFunc之类开箱即用的实现。但实践中计算整个训练集的损失函数和梯度是很慢的，极端情况下甚至无法把整个数据集装进单机内存里。批优化的另一个短处是无法在线处理新数据。随机梯度下降（ SGD ）解决了这两个问题，在跑了单个或者少量的训练样本后，便可沿着目标函数的负梯度更新参数，逼近局部最优。SGD 应用于神经网络的目标是缓解反向传播在整个训练集上的高计算成本。SGD 可以克服计算成本问题，同时保证较快的收敛速度。

随机梯度下降

标准的梯度下降算法更新目标函数 $J(\theta)$ 的参数 $\theta$ 的过程如下： 

$$ \theta = \theta – \alpha \nabla_\theta E[J(\theta)] $$  

其中，期望值 $E[J(\theta)]$ 是通过整个训练集进行估计的。而随机梯度下降（ $SGD$ ）在更新和计算参数梯度时，只简单地使用单个或者少量训练样本来估计期望值。新的更新公式定义如下，  

$$ \theta = \theta - \alpha \nabla_\theta J(\theta; x^{(i)},y^{(i)}) $$  

其中，$ (x^{(i)},y^{(i)}) $ 是训练集中的一个样本。  

通常来说， $SGD$ 中参数更新的计算不使用单个样本，而是少量或说一小批样本。这样做的原因有两个：第一，这降低了参数更新过程中的方差，使收敛的过程更稳定（Z字线不至于太离谱），第二，可以很好地将成本和梯度的计算矢量化，于是在计算中可以利用到深度优化的矩阵运算。尽管 $minibatch$ 的最佳值会因不同的应用和架构而不同，但经验$minibatch$大小是 $256$ 。  

$SGD$ 中的学习率$\alpha$值比批梯度下降的学习率小很多，因为前者在更新过程中的方差更大。选择合适的学习率和学习率变更策略是相当困难的。一个实践有效的标准做法是在迭代开始时的一两个迭代中使用一个足够小的固定学习率，以提供了稳定的收敛性。然后随着收敛速度的下降，将学习率减半。一个更好的方法是每次迭代后在预留的一组数据上计算目标函数的值，当相邻两次迭代目标函数变化值小于某个较小的阈值时，才降低学习率。这往往会很好地收敛于一个局部最优值。另一个常用的策略是，学习率设为 $\frac{a}{b+t}$ ，其中 $t$ 是迭代回合数，变量 $a$ 和 $b$ 决定了初始时的学习率。还有更先进的方法，包括回溯线搜索寻找最优更新量。 

最后，有一点需要注意的是，在 $SGD$ 中，把数据喂给算法的顺序很重要。如果数据是某种偶然的有意义的顺序，这可能会使得梯度偏离实际并导致收敛性差。为避免该问题，我们一般都会在每次迭代前对数据进行随机洗牌。  

动量

如果目标函数是一个朝着最优解的长长浅沟，在很多地方有陡峭的墙坡的话，由于负梯度指向某个陡峭的方向而不是指向最优解，标准的 $SGD$ 将在峡谷里来回振荡。深层网络结构的目标函数就是这种情况。此时，标准的 $SGD$
 收敛速度特慢，特别是在第一次迭代之后。动量是推动目标函数值朝最优解的浅沟快速下降的一种方法。动量的更新过程如下：

$$\begin{align}v &= \gamma v+ \alpha \nabla_{\theta} J(\theta; x^{(i)},y^{(i)}) \\\theta &= \theta -
 v\end{align}$$

上述方程中， $V$ 是当前的速度矢量（参数更新量），与参数向量 $\theta$ 维度相同； $\alpha$ 是学习率，在使用动量的时候，因为梯度的数量级较大，所以动量的值必须较小。最后，动量 $\gamma \in (0,1]$ 控制旧的更新量有多少会进入当前更新量。一般第一个迭代中 $\gamma$ 的值设为 $0.5$，稳定之后增加到 $0.9$ 或更高。

在Hinton老爷子的公开课中，用到了类似的动量更新：

delta = momentum * prev_delta + gradient/batchsize

卷积神经网络

概述

卷积神经网络（ $CNN$ ）具备一个或多个卷积层（常伴有池化步骤），且后面跟一个或多个全连接层的标准多层神经网络。卷积神经网络在设计上利用了输入图像的二维结构（其它的二维输入还有语音信号等）。卷积神经网络的实现是借助局部连接和在其之后的绑定权重，其中池化操作有平移不变特征。卷积神经网络的另一个优点在于更容易训练，因为卷积神经网络的参数比相同隐含单元的全连接网络要少。在本节内容中，我们将会讨论卷积神经网络的架构、用来计算梯度的反向传播算法。
  

网络架构

一个卷积神经网络是由多个卷积层（有的还附带池化层）以及最后的全连接层组成的。卷积层的输入是一个大小为 $m \times m \times r$ 的图像，其中 $m$ 是图像的宽高， $ r $ 是图像的通道个数。例如一个 $RGB$ 图像的通道数 $ r=3 $ 。卷积层有 $k$ 个大小为 $n \times n \times q$ 的滤波器（或称核），其中 $n$ 为小于图片的一个值（卷积核的大小）， $q$ 既可以与通道个数 $r$ 相同，也可能因不同的核而不同。过滤器的大小决定局部连接的结构，局部连接结构被卷积成为大小 $m-n+1$ 的 $k$ 个feature map。之后，每个feature map中的每个 $p \times p$ 的区块通常会进行平均值或最大值池化。其中 $p$ 的取值范围为从 $2$ （小图片，例如 $MNIST$ 手写数字数据集）到 $5$ （大图片）。在池化层之前或之后要加上偏置并代入 $S$ 型非线性激活函数中。下图描述了卷积神经网络中一个完整的卷积和池化层。相同颜色的单元有着相同的权重。 

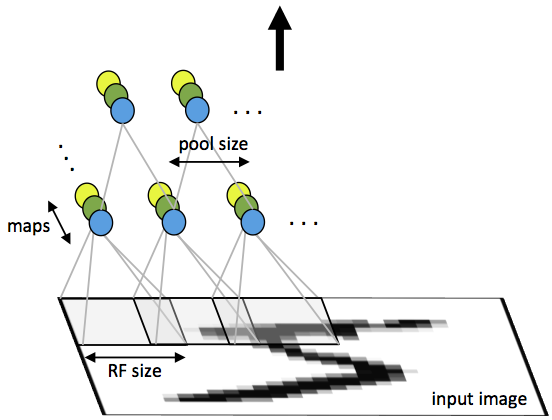
图1：一个卷积神经网络的第一层的池化过程。相同颜色的神经单元权重相同，不同颜色的神经元表示不同的滤波器

这里虽然每个feature map只画了3个单元，但实际上可能有非常多没画出来。它们的激活值共同构成一种新的特征。pool倒画得很形象，size=2，减小了连接数。

在卷积层后可能存在任意个全连接层。这些密集连接的层与常规的多层神经网络相同。

反向传播

对损失函数 $J(W,b ; x,y)$ ，定义 $\delta^{(l+1)}$ 是第 $(l+1)$ 层的误差项，其中 $(W, b)$ 是模型参数，
 $(x,y)$ 是标注训练数据。如果第 $l$ 层与第 $(l+1)$ 层是全连接的，那么第 $l$ 层的误差项为：  

$$\begin{align}   \delta^{(l)} = \left((W^{(l)})^T \delta^{(l+1)}\right) \bullet f'(z^{(l)}) 
  \end{align}$$  

损失函数关于第 $l$ 层参数的梯度为：  

$$\begin{align}   \nabla_{W^{(l)}} J(W,b;x,y) &= \delta^{(l+1)} (a^{(l)})^T, \\   \nabla_{b^{(l)}}
 J(W,b;x,y) &= \delta^{(l+1)}.\end{align}$$  

如果第 $l$ 层是一个卷积和池化层，那么误差传播的过程是：  

$$\begin{align}   \delta_k^{(l)} = \text{upsample}\left((W_k^{(l)})^T \delta_k^{(l+1)}\right) \bullet f'(z_k^{(l)}) 
  \end{align}$$  

其中， $k$ 是滤波器的编号， $f'(z_k^{(l)})$ 是激活函数的导数。upsample操作通过计算连接到到池化层的各神经元（即池化层前一层的神经元）的误差来将误差传出池化层。举个例子，对于平均值池化，upsample将误差进行简单的均匀分布（平均）返还给上一层神经元。而在最大值池化中，则把误差返还给产生最大值的上层单元，因为所有的输入都来自该神经元。
  

最后，为了计算每个 $feature\ map$ 的梯度，我们再次使用自带border handling的卷积：

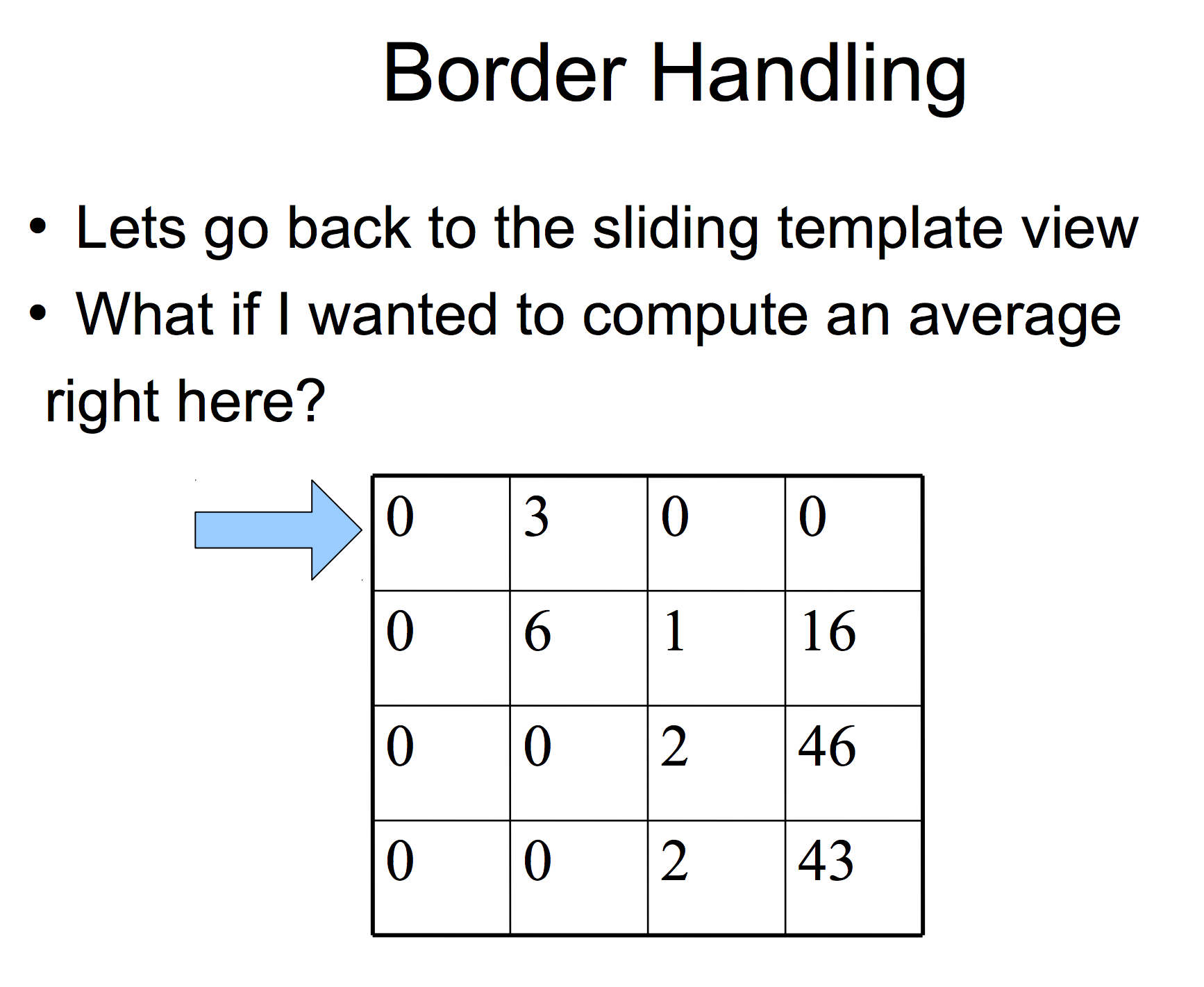
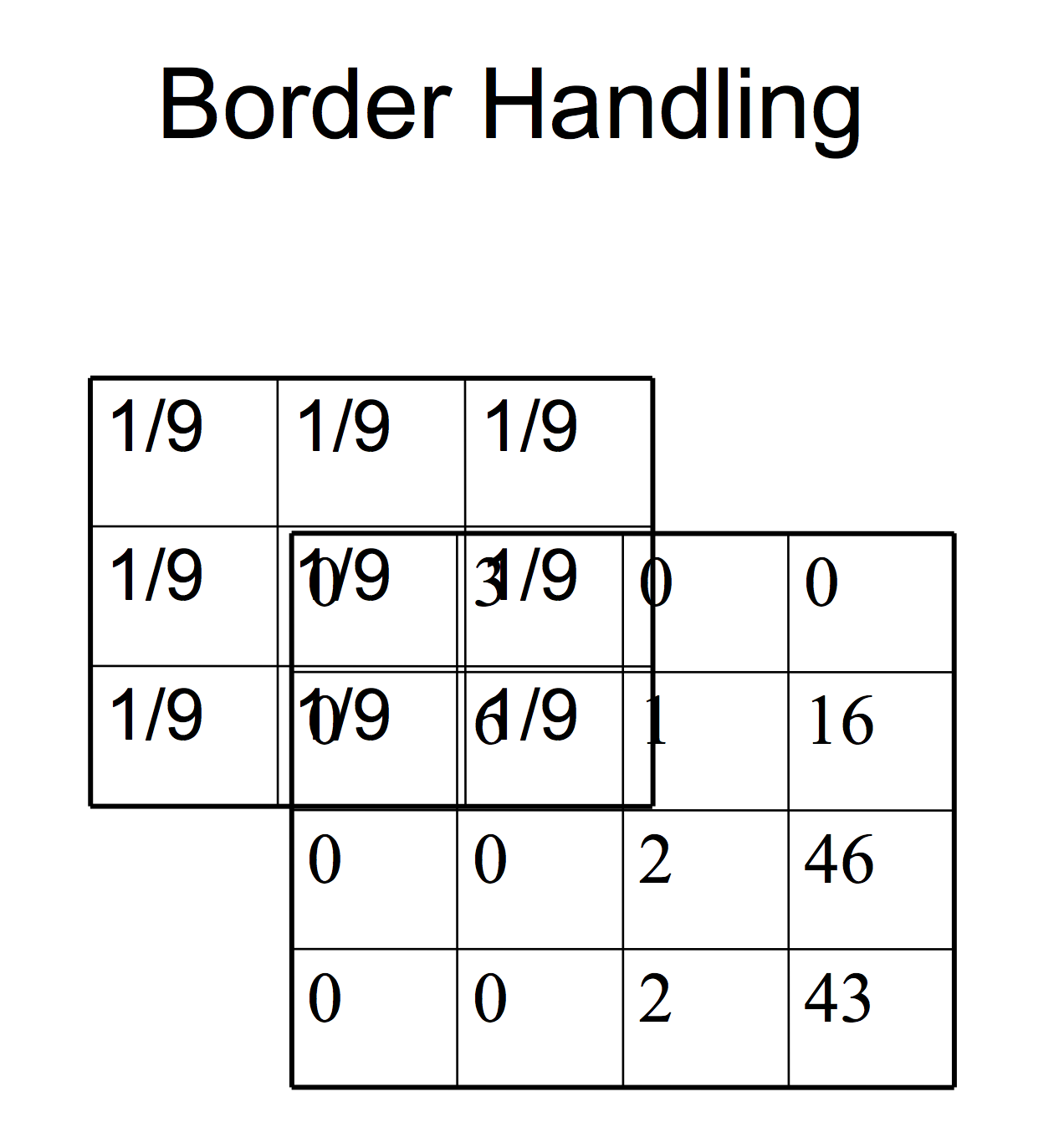
还需要翻转误差矩阵 $\delta_k^{(l)}$ ，这个过程与前向传播时计算卷积一样。

$$\begin{align}     \nabla_{W_k^{(l)}} J(W,b;x,y) &= \sum_{i=1}^m (a_i^{(l)}) \ast
 \text{rot90}(\delta_k^{(l+1)},2), \\     \nabla_{b_k^{(l)}} J(W,b;x,y) &=  \sum_{a,b}
 (\delta_k^{(l+1)})_{a,b}.   \end{align}$$ 

其中，$a^{(l)}$是第 $l$ 层的输入，于是 $a^{(1)}$ 就是输入图像。操作 $(a_i^{(l)}) \ast \delta_k^{(l+1)}$ 是第 $l$ 层的第 $i$ 个输入关于第 $k$ 个滤波器的卷积。

对比无卷积的普通神经网络：

$$
 \begin{align}
 \nabla_{W^{(l)}} J(W,b;x,y) &= \delta^{(l+1)} (a^{(l)})^T, \\
 \nabla_{b^{(l)}} J(W,b;x,y) &= \delta^{(l+1)}.
 \end{align}
    $$

发现多了滤波器的编号，然后$\nabla_{W^{(l)}} J(W,b;x,y)$多了个对误差项$\delta_k^{(l+1)}$的翻转操作（不是卷积操作，卷积其实就是$Wx+b$，会按照普通的神经元连接求导处理）。

 知识共享署名-非商业性使用-相同方式共享：码农场 » 随机梯度下降与卷积神经网络