码农场本文按照调用顺序抽丝剥茧地分析了CRF++的代码，详细注释了主要函数，并指出了代码与理论公式的对应关系。内容包括拟牛顿法的目标函数、梯度、L2正则化、L-BFGS优化、概率图构建、前向后向算法、维特比算法等。
背景知识请参考《条件随机场》。
训练
先从训练开始说起吧
/** * 命令行式训练 * @param argc 命令个数 * @param argv 命令数组 * @return 0表示正常执行,其他表示错误 */ int crfpp_learn(int argc, char **argv)
该函数解析命令行之后调用：
/** * 训练CRF模型 * @param param 参数 * @return */ int crfpp_learn(const Param ¶m)
该函数会调用：
/** * 训练 * @param templfile 模板文件 * @param trainfile 训练文件 * @param modelfile 模型文件 * @param textmodelfile 是否输出文本形式的模型文件 * @param maxitr 最大迭代次数 * @param freq 特征最低频次 * @param eta 收敛阈值 * @param C cost-factor * @param thread_num 线程数 * @param shrinking_size * @param algorithm 训练算法 * @return */ bool learn(const char *templfile, const char *trainfile, const char *modelfile, bool textmodelfile, size_t maxitr, size_t freq, double eta, double C, unsigned short thread_num, unsigned short shrinking_size, int algorithm);
该函数先读取特征模板和训练文件
/** * 打开配置文件和训练文件 * @param template_filename * @param train_filename * @return */ bool open(const char *template_filename, const char *train_filename);
这个open方法并没有构建训练实例，而是简单地解析特征模板和统计标注集：
/** * 读取特征模板文件 * @param filename * @return */ bool openTemplate(const char *filename); /** * 读取训练文件中的标注集 * @param filename * @return */ bool openTagSet(const char *filename);
回到learn方法中来，做完了这些诸如IO和参数解析之后，learn方法会根据算法参数的不同而调用不同的训练算法。取最常用的说明如下：
/** * CRF训练 * @param x 句子列表 * @param feature_index 特征编号表 * @param alpha 特征函数的代价 * @param maxitr 最大迭代次数 * @param C cost factor * @param eta 收敛阈值 * @param shrinking_size 未使用 * @param thread_num 线程数 * @param orthant 是否使用L1范数 * @return 是否成功 */ bool runCRF(const std::vector<TaggerImpl *> &x, EncoderFeatureIndex *feature_index, double *alpha, size_t maxitr, float C, double eta, unsigned short shrinking_size, unsigned short thread_num, bool orthant)
计算梯度
创建多个CRFEncoderThread，平均地将句子分给每个线程。每个线程的工作其实只是计算梯度：
/** * 计算梯度 * @param expected 梯度向量 * @return 损失函数的值 */ double TaggerImpl::gradient(double *expected)
梯度计算时，先构建网格：
void TaggerImpl::buildLattice()
由于CRF是概率图模型，所以有一些图的特有概念，如顶点和边：
/** * 图模型中的节点 */ struct Node /** * 边 */ struct Path
buildLattice方法调用rebuildFeatures对每个时刻的每个状态分别构造边和顶点：
for (size_t cur = 0; cur < tagger->size(); ++cur)
{
const int *f = (*feature_cache)[fid++];
for (size_t i = 0; i < y_.size(); ++i)
{
Node *n = allocator->newNode(thread_id);
n->clear();
n->x = cur;
n->y = i;
n->fvector = f;
tagger->set_node(n, cur, i);
}
}
for (size_t cur = 1; cur < tagger->size(); ++cur)
{
const int *f = (*feature_cache)[fid++];
for (size_t j = 0; j < y_.size(); ++j)
{
for (size_t i = 0; i < y_.size(); ++i)
{
Path *p = allocator->newPath(thread_id);
p->clear();
p->add(tagger->node(cur - 1, j), tagger->node(cur, i));
p->fvector = f;
}
}
}
这也就是大家经常看到的类似如下的图：
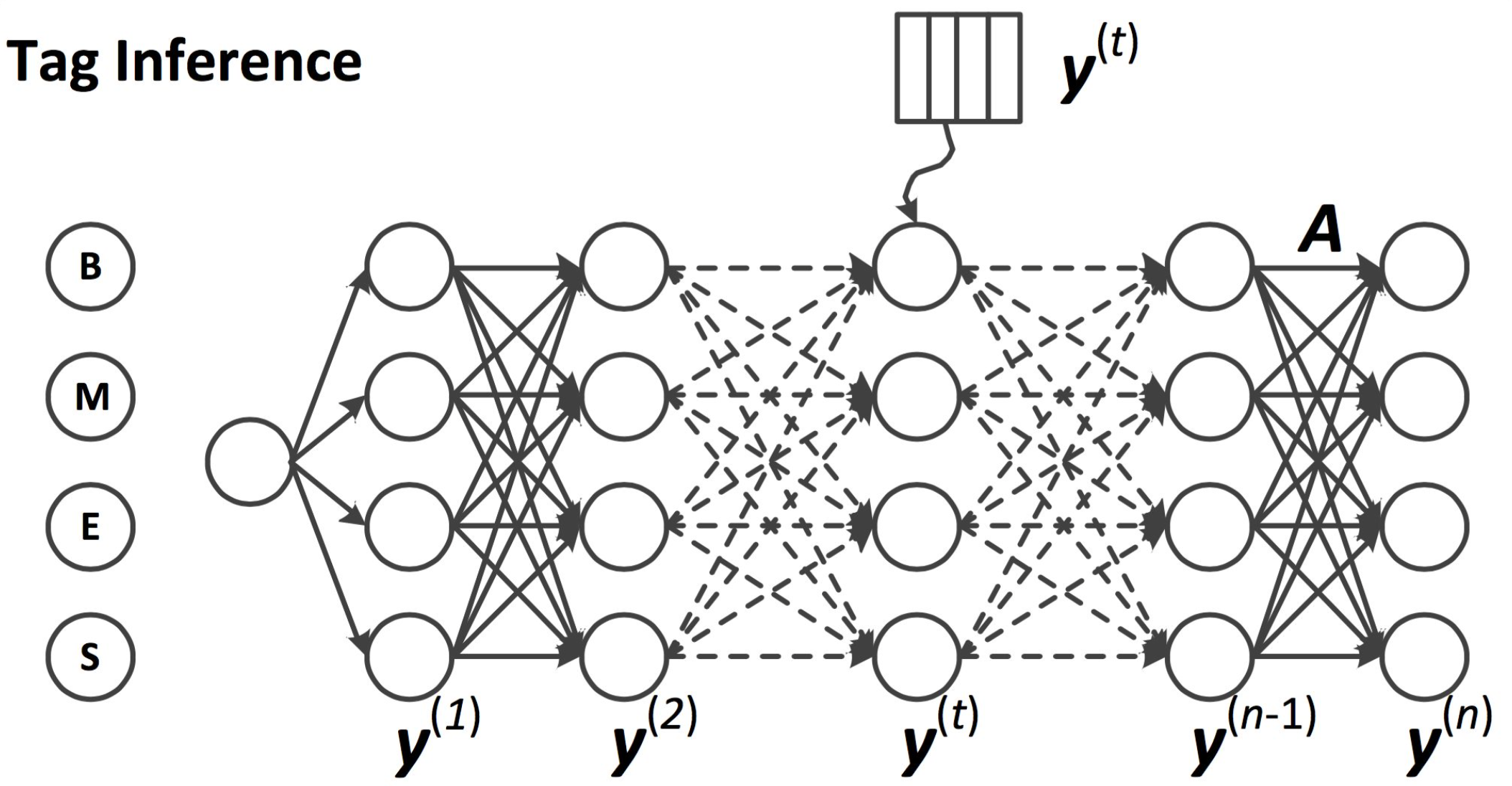
然后计算每个节点和每条边的代价（也就是特征函数乘以相应的权值，简称代价）：
/**
* 计算状态特征函数的代价
* @param node 顶点
*/
void FeatureIndex::calcCost(Node *n) const
{
n->cost = 0.0;
#define ADD_COST(T, A) \
do { T c = 0; \
for (const int *f = n->fvector; *f != -1; ++f) { c += (A)[*f + n->y]; } \
n->cost =cost_factor_ *(T)c; } while (0)
if (alpha_float_)
{
ADD_COST(float, alpha_float_);
}
else
{
ADD_COST(double, alpha_);
}
#undef ADD_COST
}
/**
* 计算转移特征函数的代价
* @param path 边
*/
void FeatureIndex::calcCost(Path *p) const
{
p->cost = 0.0;
#define ADD_COST(T, A) \
{ T c = 0.0; \
for (const int *f = p->fvector; *f != -1; ++f) { \
c += (A)[*f + p->lnode->y * y_.size() + p->rnode->y]; \
} \
p->cost =cost_factor_*(T)c; }
if (alpha_float_)
{
ADD_COST(float, alpha_float_);
}
else
{
ADD_COST(double, alpha_);
}
}
其中fvector是当前命中特征函数的起始id集合，对于每个起始id，都有连续标签个数种y值；n->y是当前时刻的标签，由于每个特征函数都必须同时接受x和y才能决定输出1或0，所以要把两者加起来才能确定最终特征函数的id。用此id就能在alpha向量中取到最终的权值，将权值累加起来，乘以一个倍率（也就是所谓的代价参数cost_factor），得到最终的代价cost。
对于边来说，也是类似的，只不过对每个起始id，都有连续标签个数平方种y值组合。
这部分对应
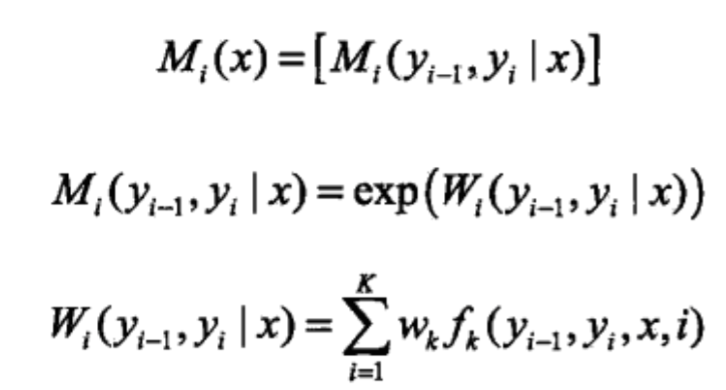
前向后向算法
网格建完了，就可以在这个图上面跑前向后向算法了:
/** * 前向后向算法 */ void forwardbackward();
该方法依次计算前后向概率：
for (int i = 0; i < static_cast<int>(x_.size()); ++i)
{
for (size_t j = 0; j < ysize_; ++j)
{
node_[i][j]->calcAlpha();
}
}
for (int i = static_cast<int>(x_.size() - 1); i >= 0; --i)
{
for (size_t j = 0; j < ysize_; ++j)
{
node_[i][j]->calcBeta();
}
}
计算前向概率的具体实现是：
void Node::calcAlpha()
{
alpha = 0.0;
for (const_Path_iterator it = lpath.begin(); it != lpath.end(); ++it)
{
alpha = logsumexp(alpha, (*it)->cost + (*it)->lnode->alpha, (it == lpath.begin()));
}
alpha += cost;
}
其中cost是我们刚刚计算的当前节点的M_i(x)，而alpha则是当前节点的前向概率。lpath是入边，如代码和图片所示，一个顶点可能有多个入边。
对应：
后向概率同理略过。
前后向概率都有了之后，计算规范化因子：
Z_ = 0.0;
for (size_t j = 0; j < ysize_; ++j)
{
Z_ = logsumexp(Z_, node_[0][j]->beta, j == 0);
}
对应着
关于函数logsumexp的意义，请参考《计算指数函数的和的对数》。
于是完成整个前后向概率的计算。
期望值的计算
节点期望值
所谓的节点期望值指的是节点对应的状态特征函数关于条件分布
的数学期望。
for (size_t i = 0; i < x_.size(); ++i)
{
for (size_t j = 0; j < ysize_; ++j)
{
node_[i][j]->calcExpectation(expected, Z_, ysize_);
}
}
calcExpectation具体实现是：
/**
* 计算节点期望
* @param expected 输出期望
* @param Z 规范化因子
* @param size 标签个数
*/
void Node::calcExpectation(double *expected, double Z, size_t size) const
{
const double c = std::exp(alpha + beta - cost - Z);
for (const int *f = fvector; *f != -1; ++f)
{
expected[*f + y] += c;
}
for (const_Path_iterator it = lpath.begin(); it != lpath.end(); ++it)
{
(*it)->calcExpectation(expected, Z, size);
}
}
第一个for对应下式的求和
概率求和意味着得到期望。
第二个for对应边的期望值。
边的期望值
所谓边的期望指的是边对应的转移特征函数关于条件分布的数学期望。
/**
* 计算边的期望
* @param expected 输出期望
* @param Z 规范化因子
* @param size 标签个数
*/
void Path::calcExpectation(double *expected, double Z, size_t size) const
{
const double c = std::exp(lnode->alpha + cost + rnode->beta - Z);
for (const int *f = fvector; *f != -1; ++f)
{
expected[*f + lnode->y * size + rnode->y] += c;
}
}
对应下式的求和
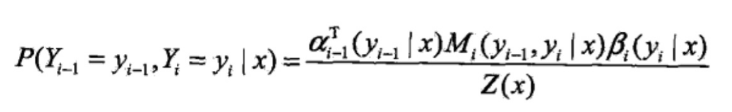
这样就得到了条件分布的数学期望：
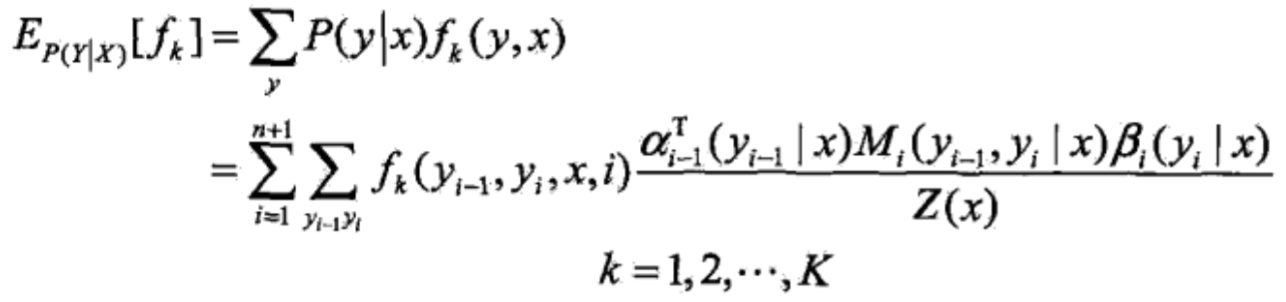
梯度计算
for (size_t i = 0; i < x_.size(); ++i)
{
for (const int *f = node_[i][answer_[i]]->fvector; *f != -1; ++f)
{
--expected[*f + answer_[i]];
}
s += node_[i][answer_[i]]->cost; // UNIGRAM cost
const std::vector<Path *> &lpath = node_[i][answer_[i]]->lpath;
for (const_Path_iterator it = lpath.begin(); it != lpath.end(); ++it)
{
if ((*it)->lnode->y == answer_[(*it)->lnode->x])
{
for (const int *f = (*it)->fvector; *f != -1; ++f)
{
--expected[*f + (*it)->lnode->y * ysize_ + (*it)->rnode->y];
}
s += (*it)->cost; // BIGRAM COST
break;
}
}
}
–expected表示模型期望（条件分布）减去观测期望，得到目标函数的梯度：
有人可能要问了，expected的确存的是条件分布的期望，但观测期望还没计算呢，把条件分布的期望减一是干什么？
这是因为对观测数据（训练数据）来讲，它一定是对的，也就是在y!=answer_[i]的时候概率为0，在y=answer_[i]的时候概率为1，乘以特征函数的输出1，就等于1，这就是观测期望。
维特比算法
紧接着gradient函数还顺便调了一下TaggerImpl::viterbi：
void TaggerImpl::viterbi()
{
for (size_t i = 0; i < x_.size(); ++i)
{
for (size_t j = 0; j < ysize_; ++j)
{
double bestc = -1e37;
Node *best = 0;
const std::vector<Path *> &lpath = node_[i][j]->lpath;
for (const_Path_iterator it = lpath.begin(); it != lpath.end(); ++it)
{
double cost = (*it)->lnode->bestCost + (*it)->cost + node_[i][j]->cost;
if (cost > bestc)
{
bestc = cost;
best = (*it)->lnode;
}
}
node_[i][j]->prev = best;
node_[i][j]->bestCost = best ? bestc : node_[i][j]->cost;
}
}
double bestc = -1e37;
Node *best = 0;
size_t s = x_.size() - 1;
for (size_t j = 0; j < ysize_; ++j)
{
if (bestc < node_[s][j]->bestCost)
{
best = node_[s][j];
bestc = node_[s][j]->bestCost;
}
}
for (Node *n = best; n; n = n->prev)
{
result_[n->x] = n->y;
}
cost_ = -node_[x_.size() - 1][result_[x_.size() - 1]]->bestCost;
}
其中prev构成一个前驱数组，在动态规划结束后通过prev回溯最优路径的标签y，存放于result数组中。
跑viterbi算法的目的是为了评估当前模型的准确度，以辅助决定是否终止训练。
正则化
为了防止过拟合，CRF++采用了L1或L2正则化：
if (orthant)
{ // L1
for (size_t k = 0; k < feature_index->size(); ++k)
{
thread[0].obj += std::abs(alpha[k] / C);
if (alpha[k] != 0.0)
{
++num_nonzero;
}
}
}
else
{
num_nonzero = feature_index->size();
for (size_t k = 0; k < feature_index->size(); ++k)
{
thread[0].obj += (alpha[k] * alpha[k] / (2.0 * C));
thread[0].expected[k] += alpha[k] / C;
}
}
以L2正则为例，L2正则在目标函数上加了一个正则项：
+
其中，
是一个常数，在CRF++中其平方被称作cost-factor，
控制着惩罚因子的强度。可见要最小化目标函数，正则化项也必须尽量小才行。模型参数的平方和小，其复杂度就低，于是就不容易过拟合。关于L1、L2正则化推荐看Andrew Ng的ML公开课。
目标函数加了一项之后，梯度顺理成章地也应加上的导数：
+
这也就是代码中为什么要自加这两项的原因了：
thread[0].obj += (alpha[k] * alpha[k] / (2.0 * C)); thread[0].expected[k] += alpha[k] / C;
L-BFGS优化
梯度和损失函数有了，之后就是通用的凸函数LBFGS优化了。CRF++直接将这些参数送入一个LBFGS模块中：
if (lbfgs.optimize(feature_index->size(), &alpha[0], thread[0].obj, &thread[0].expected[0], orthant, C) <=
0)
{
return false;
}
据说这个模块是用一个叫f2c的工具从FORTRAN代码转成的C代码，可读性并不好，也就不再深入了。
// lbfgs.c was ported from the FORTRAN code of lbfgs.m to C // using f2c converter // // http://www.ece.northwestern.edu/~nocedal/lbfgs.html
有兴趣的话看看《数值优化：理解L-BFGS算法》即可。
预测
预测就简单多了，主要对应下列方法：
bool TaggerImpl::parse()
{
CHECK_FALSE(feature_index_->buildFeatures(this)) << feature_index_->what();
if (x_.empty())
{
return true;
}
buildLattice();
if (nbest_ || vlevel_ >= 1)
{
forwardbackward();
}
viterbi();
if (nbest_)
{
initNbest();
}
return true;
}
主要的方法也就是建立网格和维特比这两个，由于前面训练的时候已经分析过，这里就不再赘述了。
Reference
http://mi.eng.cam.ac.uk/~cz277/doc/Slides-CRFASR-CSLT.pdf
您好，请问源码在哪里可以下载到呀
图片挂了。。。
赞！
请问一下：Node::calcException()函数中的第一行：“const double c = std::exp(alpha + beta – cost – Z)”，我理解减去cost是因为代码中的alpha变量和beta变量都含有cost，因此需要减去一个。但是这与公式P(Y=yi|x)=Alpha(yi|x)*Beta(yi|x)/Z(x)不一致，而且我在很多材料里面都看到类似的公式。按照这个公式来说貌似对应的代码是std::exp(alpha + beta – Z )，但我感觉减去一个cost似乎是有道理的。 烦请指教，多谢。
你的理解是正确的，公式毫无疑问也是正确的，只不过CRF++是这么实现的而已，每个node的α和β在实现上都加上了cost：
void Node::calcAlpha()
{
alpha = 0.0;
for (const_Path_iterator it = lpath.begin(); it != lpath.end(); ++it)
{
alpha = logsumexp(alpha, (*it)->cost + (*it)->lnode->alpha, (it == lpath.begin()));
}
alpha += cost;
}
void Node::calcBeta()
{
beta = 0.0;
for (const_Path_iterator it = rpath.begin(); it != rpath.end(); ++it)
{
beta = logsumexp(beta, (*it)->cost + (*it)->rnode->beta, (it == rpath.begin()));
}
beta += cost;
}
所以多了一个cost。
请教一下大神，我在用CRF训练大的语料时，比如20万的语料，要19个小时。。有并行的CRF分词器吗？还有一个问题，CRF支持增量训练模型吗？我要优化CRF，又要重新训练一遍是吗？这个好浪费时间呀。。。
快速训练用crfsgd
并行的CRF分词：https://github.com/hankcs/HanLP
增量训练可以实现，无非是用旧模型的参数作为新模型的初始参数。但暂未看到开源实现。
好的，谢谢。我试试crfgd的训练。还有就是，比如要优化统计分词，发现badcase，将badcase正确标注好，放到之前的语料中重新训练是吗？
你好，我看了crfsgd，CRFsuite都是一些词性标注的demo，分词的没有找到。
不错，最近也在看这个