Hinton神经网络公开课10 Combining multiple neural networks to improve generalization

Full Bayesian Learning

复习一下，贝叶斯学习的思想是，不再去找单个的最优参数集，而是输出定义在所有可能的参数集上的后验概率分布。这是个计算压力极大的任务。

有了后验概率分布后，就能得到所有模型的输出的期望。这也是个计算压力大的任务。

Full Bayesian Learning允许在较少数据量（计算压力小）的情况下训练复杂的模型。

过拟合：频率学派的解释

数据量小，无法得到完整的后验概率分布，应当采用简单一些的模型。这种说法仅仅在“以找到最佳参数为目标”的前提下成立。如果你有了参数上的完整后验概率分布，就不会有过拟合的问题了。随着数据量增多，概率会分布到越来越少的几组参数集上去。反之，许多参数的概率都很大，模型的输出非常模糊。

一个经典的过拟合例子

要拟合这6个点，你相信哪个模型？

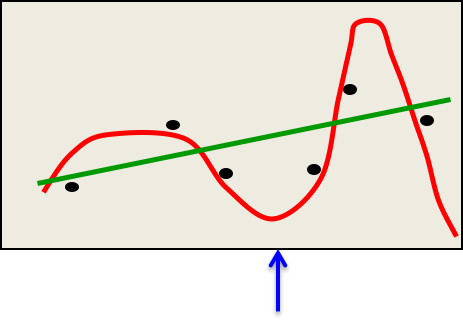
有6个参数的多项式模型拟合得更好，但它就是不可信，也不经济，也会做出愚蠢的预测（蓝色箭头处就是一个愚蠢的预测）。

如果我们计算5阶多项式模型的所有参数的分布，以越厚的线表示越大的概率，则可能得到下图：

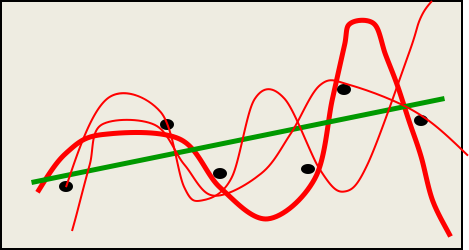
于是我们就能得到更模糊但更可信的预测，虽然有些曲线没有通过一些点，但非常接近，也没有做出疯狂的预测。在蓝色箭头处，许多模型的预测相差甚远，但均值会非常接近绿线。

前面说的“数据量少则模型应该简单”是不合贝叶斯学派的理念的，数据量不应该影响我们关于模型复杂度的先验。一个虔诚的贝叶斯学派人士会说，模型复杂度是先于数据量而确定的，你之所以不愿意用复杂度高的模型，只是因为你没有收集到足够的数据而已。

神经网络中近似full Bayesian learning 

如果神经网络参数较少，则可以在参数空间的每个区块都计算一次$p(W|D)$，以此后验概率衡量此参数集拟合数据的程度。

• 计算上很昂贵，但没有涉及到梯度下降，也没有局部最优解的限制

当计算出所有格点上的概率后，就可以将其综合起来在测试数据上做预测。当数据量不足的时候，这比机器学习优化方法得到的模型效果更好，虽然计算上依然很昂贵。

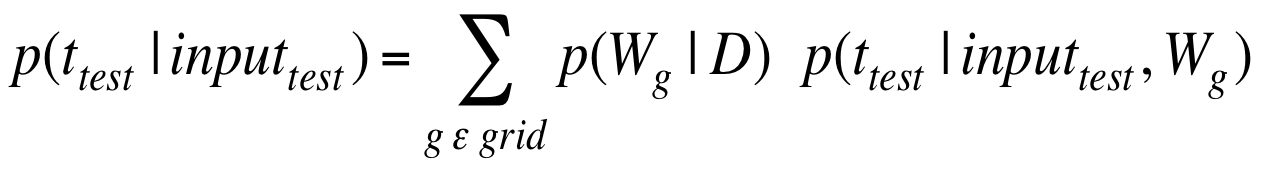
公式上是参数的后验概率乘以在此参数下模型输出结果的概率之和。

full Bayesian learning示例

下图是一个4节点的简单网络：

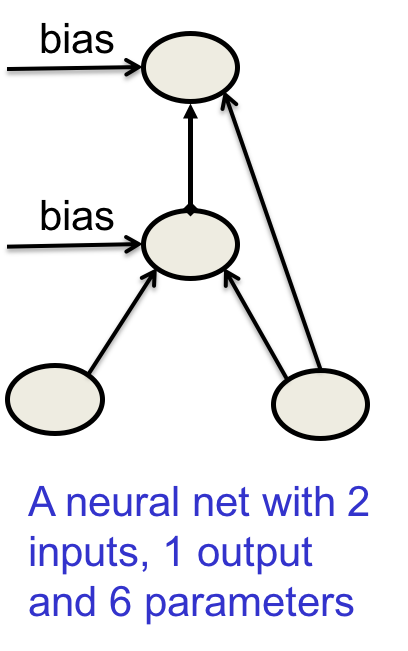
每个参数取值范围为$\{-2, -1.5, -1, -0.5, 0 ,0.5, 1, 1.5, 2\}$这9个值。

• 那么参数空间中一共有$9^6$个格点。

• 每个格点都需要计算所有训练实例输入map到输出的概率

• 乘上格点的先验概率，归一化得到每个格点（参数集）的后验概率

• 利用该后验概率来加权平均每个格点下的预测输出

让full Bayesian learning 可行

上一节最后演示的简单神经网络上的full Bayesian learning 已经够复杂了，实践中的参数向量上百万维，如何才能计算可行呢？

当一个格点维度太高时

格点的数量与参数向量的维度成指数关系。如果数据量足够降低大部分参数向量的概率，只留下一小部分能够显著参与到最终结果的大概率参数向量的话，我们可以只考虑这一小部分。核心思想是，也许只根据后验概率来采样参数向量就足够了。

也就是上图的绿框。我们根据该概率来决定是否采样这个参数向量，0或1，期望由概率决定。

采样权值向量

在标准的反向传播中，我们沿着减小损失函数的方向持续移动。weight space如下图所示：

曲面上有很多凹陷的“碗”，碗底含有一个个局部最优解。梯度下降的方向是增大所有训练实例上的对数似然以及对数先验之和。最终的结果是要么达到局部最优，要么在某个高原上卡住，或者移动如此之慢以致于失去耐心。这张图要表达的意思是，我们从一个初始点开始，按照一条路径抵达最终点。

采样参数向量的一种方法

假设我们在每次更新后都往权值向量上加入一些高斯噪音，于是移动的方向不再固定，而是四处漫游；但倾向于选择那些海拔较低的方向。

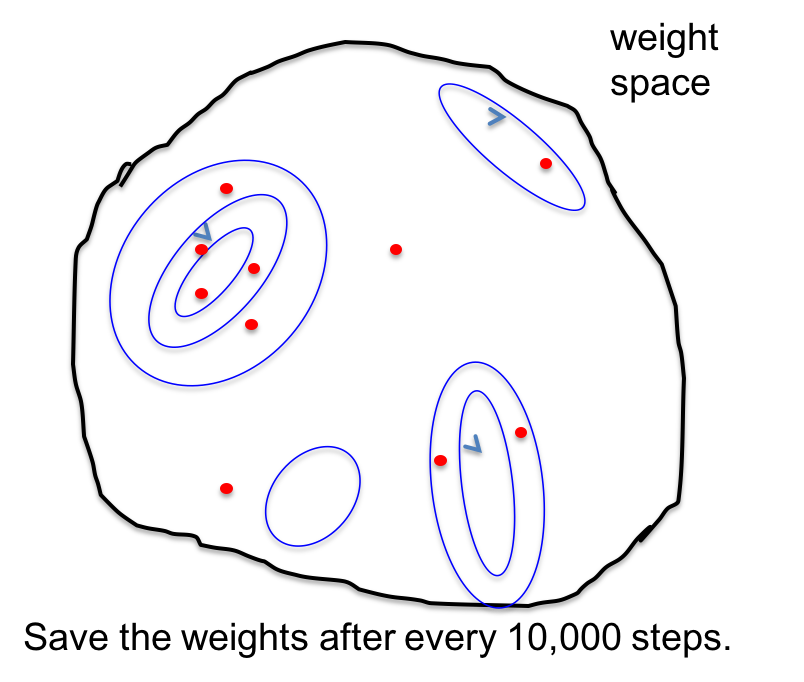
我们可以主动控制采样某参数向量的概率。红点是我们希望采样的参数向量，它们大部分都分布在低代价的区域，少部分分布在高代价的高原上。因为这些高原实在太大了。峡谷最深处有最多的红点，其他浅处也有一些，因为这是噪声采样。

马尔科夫蒙特卡洛方法的性质

如果噪音量得到，在参数向量游走了足够长的间隔取一次样的话，则将得到参数空间上的真实后验分布下的一个样本。这被称作马尔科夫蒙特卡洛法（MCMC）。这使得大规模神经网络上的full Bayesian learning 变得可行。

还有一些更复杂但更高效的MCMC变种。这里的高效指的是，只需要游走更少的步骤就能执行采样。

Full Bayesian learning 与mini-batch

Full Bayesian learning 还能与mini-batch搭配使用。如果我们在随机的mini-batch上计算代价函数的梯度的话，我们会得到含有噪音的无偏见样本。这个噪音正好可以提供给需要噪音的MCMC！Ahn, Korattikara &Welling (ICML 2012)展示了这样一种高效可行的方法。

Dropout:一种高效的训练方法

这是一种综合大量神经网络，却不需要单独训练大量神经网络模型的新方法。通过在每个训练实例上，随机忽略一些节点，可以认为这是一个不同的网络架构。问题是，如何仅利用一个实例训练一个神经网络？如何在预测的时候将它们综合起来？答案是大量利用权值共享。

两种平均模型的方法

混合：平均模型输出的概率。

乘积：取输出概率的几何均值（相乘、开方、归一化）。

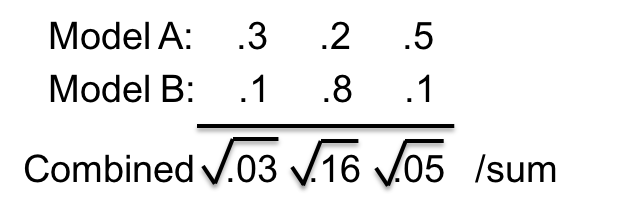
在乘积方式下，一个模型的小概率的输出往往有“一票否决”的效果。

Dropout：一种高效平均多个大规模神经网络的方法

这是一种贝叶斯学习方法的近似替代，可能没有本物效果那么好，但效率更高更可行。

考虑如下只有一个隐藏层的神经网络：

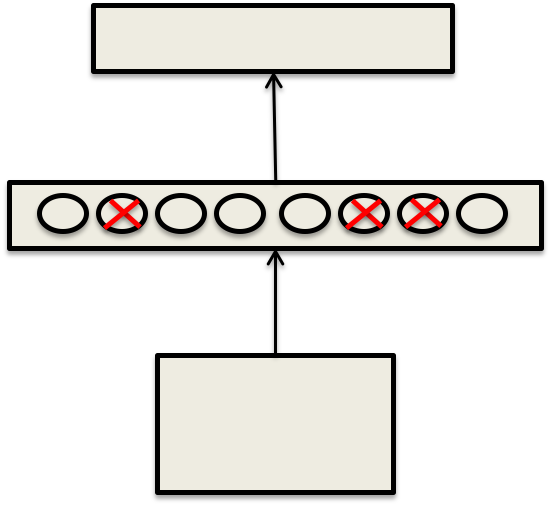
每遇到一个训练实例，对每个隐藏单元我们以0.5的概率随机忽略掉它（当它缺失、不存在）。这等效于从$2^H$个不同网络架构中随机采样一个，H是隐藏单元的个数。这是个大数字，幸运的是所有网络架构都共享参数。

将Dropout视作平均模型

我们从$2^H$个不同模型中采样，大部分模型从未被采样出来，而每个模型只得到一个训练实例。这是bagging的一个极端例子。

权值的共享意味着每个模型都被强烈地正则化了（因为参数重复就是一种正则）。这比把权值限定在原点附近的L1或L2正则要好得多。

预测时怎么办？

我们可以采样许多不同的网络架构，然后取它们输出的几何平均，但这样计算太复杂了。

更好的方法是使用所有的隐藏单元，但把它们的出度权值减半，于是输出的期望就与采样时保持一致了。

另外，只要使用softmax层，则上述做法等效于求$2^H$个模型输出的几何平均。

如果有多个隐藏层

• 可以在每一层都用0.5的Dropout

• 在预测的时候，同样使用所有单元，只不过输出权值减半

• 这虽然不再是等效的，却是一种高效的近似

这被称作mean net。

当然也可以直接采样多个模型的输出，这样做的好处是，答案将含有不确定性（暂时不知道好在哪里）。

输入层也能Dropout吗

也可以，但保留输入单元的概率要设置得高一点。

Dropout的效果

非常好。特别是当深度神经网络显著地过拟合的时候。任何使用“early stopping”的网络，都可以用Dropout替代来取得更加效果，代价是需要多花一点训练时间、多一点隐藏节点。

那如果你的神经网络没有过拟合怎么办呢？那就多加一些隐藏节点让它过拟合，然后用Dropout！

另一种视角

这是老爷子如何发明Dropout的逸话。

混合专家模型时，是什么妨碍了模型的“专业化”呢？如果一个隐藏单元知道其他单元的输出是错的，则它可能在另一个矫枉过正的方向上尝试中和它们的输出。这种复杂协作方式在新数据上效果不佳。人类社会也有类似的情况，如果一个组织机构过于复杂，则更容易出错。而平行的小团队全部出错的概率较小。

如果一个隐藏单元与其他单元协作良好，则很可能它本身单干也能干得很好。但它也可能是在给其他单元擦屁股。通过Dropout，提高单兵作战能力，而不是和稀泥，这就是其效果好的原因。

 知识共享署名-非商业性使用-相同方式共享：码农场 » Hinton神经网络公开课10 Combining multiple neural networks to improve generalization