Hinton神经网络公开课11 Hopfield nets and Boltzmann machines

这节课介绍Hopfield Nets，这是80年代神经网络复兴的主要原因之一。这种简单优美的模型将记忆储存为激活值中的模式。然后介绍带有随机隐藏单元的Stochastic Hopfield nets（即玻尔兹曼机），及其搜索算法，为下节课的训练算法打下基础。

Hopfield Nets

下面介绍一种不同的前馈神经网络，经常被称作“基于能量的模型（energy based models）”，因为有很多来自全局energy function的性质。Hopfield Nets是其中最简单的一种，由递归的二值单元构成。

非线性递归网络一般很难分析，其表现非常复杂。可能进入稳定状态，也可能震荡不止，也可能处于一种无法预测的混沌状态。但John Hopfield 发现如果连接是对称的，则存在一个全局“能量函数”。

• 每个单元取值0或1，于是整个神经网络的每组取值都对应到一个能量上去。

• 存在一个最低能量

能量函数

能量函数是这么一个东西，它由所有相连的神经网络pair贡献。每个贡献值取决于弧的权值以及两端神经元的二进制状态。

$s_i$是单元的激活值，0或1（一些变种里面可能是±1），$b_i$是偏置，$w_{ij}$是权值。

能量是个讨厌的东西，会让人长胖，低能量才是好的。

上述简单的二次能量函数还隐式地定义了，单个单元开关与否对全局能量的影响，或称“能隙”。

如果用E对$s_i$求导（不严格意义上），也会得到$\Delta E_i$，只不过多了一个负号。

能量最低点

要找到网络的最低能量，一种方法是随机选择一个初始状态，然后每次随机更新一个节点的激活值（0或1中的较小者）。举个例子，初始状态如下：

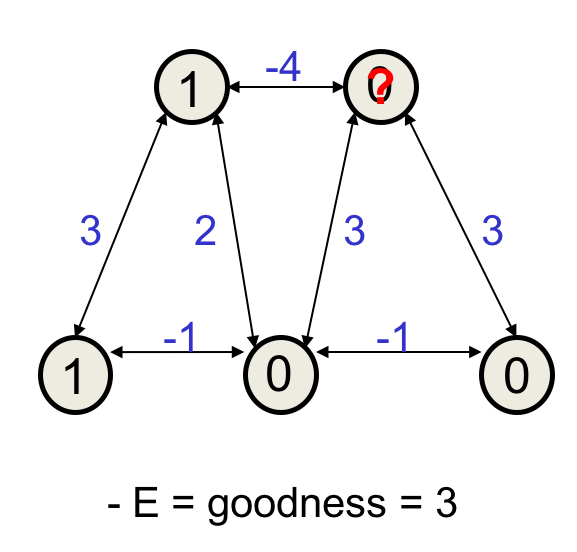
能量为-3，或说好感度为3 。计算的时候，只需要找到两端单元都是1的pair，求和即可。这里只有一个这样的弧。

接下来随机调整，对于上图的？处，选0还是1好呢？如果选1的话，好感度会成为$3-4=-1$，于是还是选0吧。

再挑一个执行优化：

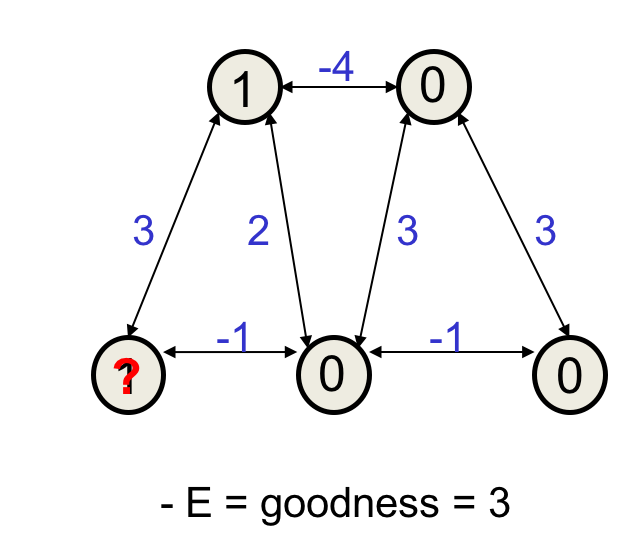
这个还是取1好。再看一个：

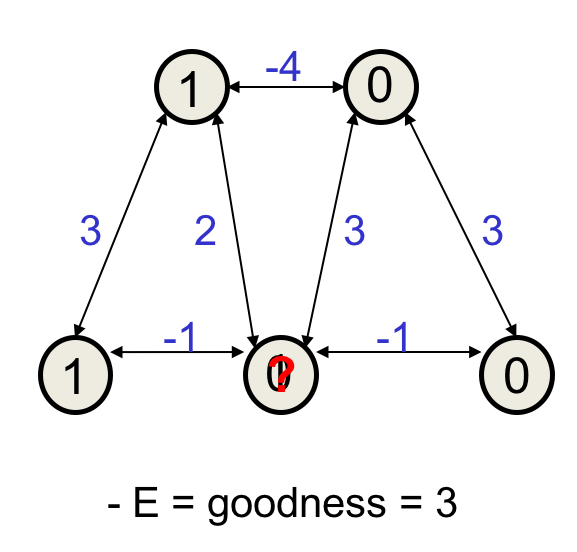
这个点取1的话，总体好感度变化量是$2-1=1$，所以应该取1。这样达到了一个能量的局部最低状态。

按这个原理尝试剩下的单元，发现都不应该改变状态，但这并不代表这达到了全局最低状态。最低的能量如下所示：

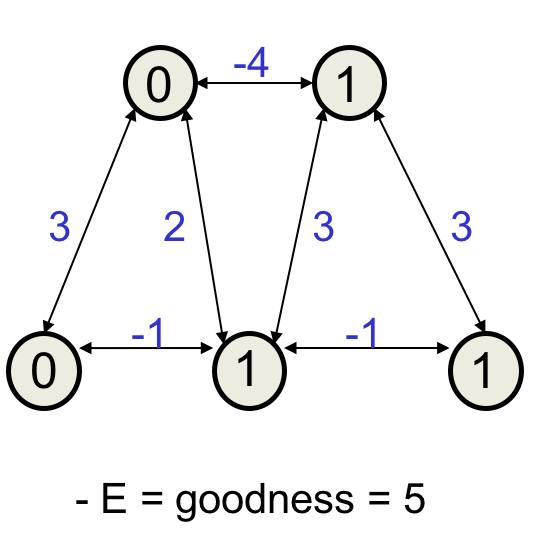
全局最低状态与上一个局部最低状态恰好是两个三角形。两个三角形是类似的，除了一条边是2另一条是3。

为何优化决策是一步步的？

如果同时优化多个节点的话，能量会上升。同时更新还会导致震荡：

每个单元的偏置都是5，弧的权值是-100。并行更新的话，每个单元都以为自己的偏置可以降低能量，于是打开自己的激活值。两者同时激活后，其弧上的权值反而使能量升高了。下次更新时，两者又同时关闭了，如此反复震荡。

这种震荡可以通过随机等待时间来消除，虽然每时刻都在同时更新多个节点，但它们下次更新的时间是随机的。

这种更新方法称作“binary theshold rule”。

一种优雅的应用

Hopfield 提出，记忆可以视作神经网络中的能量最低点。通过一些有关该记忆的模糊属性，我们设置网络中单元的初始值。然后通过binary theshold rule随机更新，最后就有可能检索到该记忆（最低点）。这是个很棒的特性，你只需要回忆一个概念的部分属性，你就能最终想起这个概念。

Hopfield Net还能抵御硬件损坏，就算移除一些节点，系统仍然稳健。心理学家会说这有点像由化石重建恐龙。给定少量节点，弧上的权值说明了剩下的节点将要如何与其搭配，最终能还原所有节点。

在Hopfield Net中储存记忆

如果要储存一个二值状态的向量，在使用±1作为激活值的情况下，则只需将初始状态设为该向量，然后对任意一对单元将其权值增加激活值之积即可：

当然，偏置视作来自一个永远激活的单元。

这个简单的更新公式不需要错误驱动，既是优点又是缺点。优点是在线学习，缺点是无法有效地储存记忆。

在使用0和1作为激活值的情况下，更新公式稍微复杂一点：

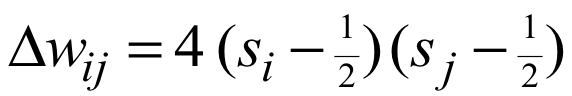
spurious minima

Hopfield Net网络的容量受限于spurious minima，这种伪最小值产生原因是两个能量最小点的合并。消除这种spurious minima比Hopfield Net本身要复杂很多。

Hopfield Net的容量

根据Hopfield的容量规则，有N个节点的全连接Hopfield网络的容量是0.15N单位的记忆，再多就会变模糊。这里一单位的记忆指的是N个二值单元的状态向量，所以容量是$0.15N^2$比特。该容量与权值无关，说明浪费掉了储存权值的比特。

我们算算计算机储存网络花费了多少比特。网络有$N^2$个权值和偏置，在储存M单位记忆后，每个权值会分布到$[-M,M]$之间（这是因为在储存记忆的过程中，总是加一或减一）。所以所需的总比特数是$N^2\log(2M+1)$。

对比Hopfield提出的$0.15$这个比例，上述对数衰减才更值得关注。

spurious minima限制了容量

每次网络记忆一个二值向量的时候，都试图创建一个新的能量最低点。以能量为纵轴，二值state为横轴做一个state space：

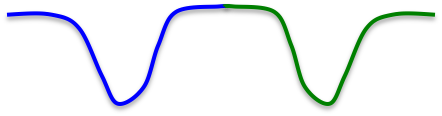
蓝绿两种pattern都有一个能量最低点。但如果两者太靠近了，则在记忆的过程中可能会合并为一个错误的最低点：

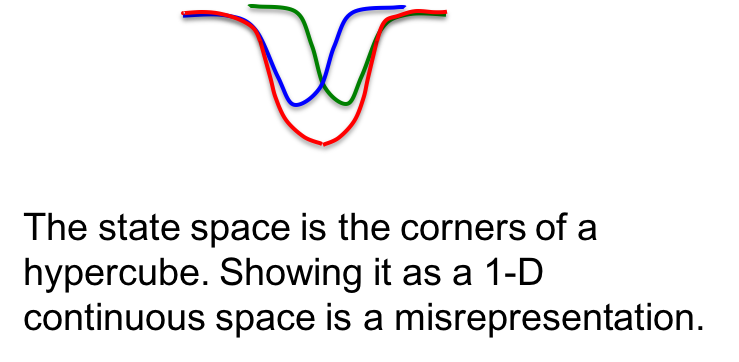
这意味着两个记忆混淆了，这就是Hopfield Net的记忆容量。

通过unlearning防止spurious minima

Hopfield等人提出了如下策略：

以随机初始状态让网络稳定下来，然后做unlearning。unlearning指的是storage rule的逆过程。这会消除过深的spurious minima并增加记忆容量。他们试验证明这种策略有效，但没有解释究竟发生了什么。

Francis Crick（DNA发现者之一）提出unlearning可能与生物在REM睡眠（快速动眼期）做的事情相同。人类一天记忆了很多东西，并产生了spurious minima。在这种睡眠状态下，人脑进入随机状态、稳定下来然后unlearning一些记忆。人会做很多梦，但早上起来的时候这些梦大部分都被遗忘了，只剩下少数醒前的梦还残留了一点记忆。既然做梦的目的不是记下来，那大脑为什么做梦呢？做梦是个矛盾的过程，做梦时大脑状态与清醒时十分类似，除了其不再由真实的生理刺激驱动，而是由真实生理刺激的下一级器官——丘脑驱动。Crick的理论（假说）在功能上解释了做梦的意义，就是消除spurious minima。

回到计算机科学上来，unlearning具体的量应当是多少呢？

按照通用的套路，必须有一个衡量模型效果的函数，然后求关于unlearning的梯度。

增加Hopfield Net的容量

在回答上述问题前，先介绍一下物理学家的发现。物理学家特喜欢用已知的数学解释大脑工作原理这种主意，也就是说找不到工作的物理学博士后终于可以在脑神经领域谋生了（哈哈）。在物理学期刊上有大量讨论Hopfield Net及其容量的文章，终于让Elizabeth Gardiner 找到了一个可以利用上权值的更好的storage rule，这个rule对大众来讲也更熟悉。

不再一锤定音地储存二值向量，而是在训练集上迭代多次。这会失去在线学习这一优势，但增大了容量。这种方法是给定向量中的其他元素，使用感知机收敛过程训练某一元素对应的单元。具体做法是，将网络设置为某一个记忆状态。然后拿出一个个节点，调整该节点上的整数权值使得该网络的能量最低。统计学家称其为“pseudo-likelihood”，这是一种在高维weight space中，固定其他维度，单独优化某一维的方法。与通常的感知机不同的是，weight是对称的，必须对每个weight计算两组梯度然后取平均。

带隐藏单元的Hopfield Nets 

这节讲了利用隐藏单元表示Hopfield Nets中可见单元（输入）的方法，权值定义了这种表示的约束。

Hopfield Nets的另一种计算角色

Hopfield Nets有两个设计思想，一是通过对称连接的二值单元网络可以找到能量最低点；二是能量最低点可能代表着记忆。

另一种思想是不再储存能量最低点或记忆，而是用隐藏单元来构建输入的interpretation表示。输入由可见单元表示，而高级的interpretation由隐藏单元的状态表示：

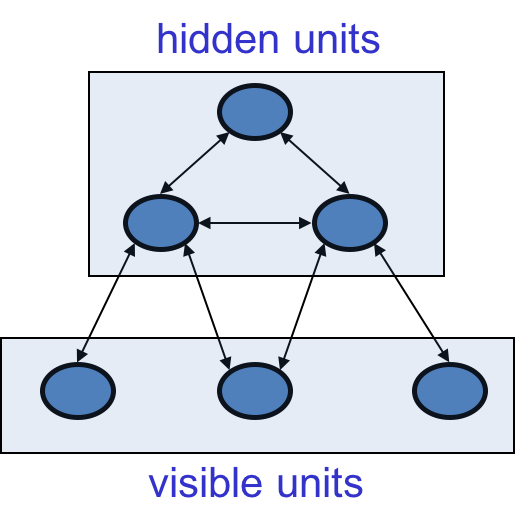
整个网络的能量代表着这种interpretation的糟糕程度，于是目标是降低能量，找到一个好的interpretation。

举个例子：从图片的2D线条推断3D边缘

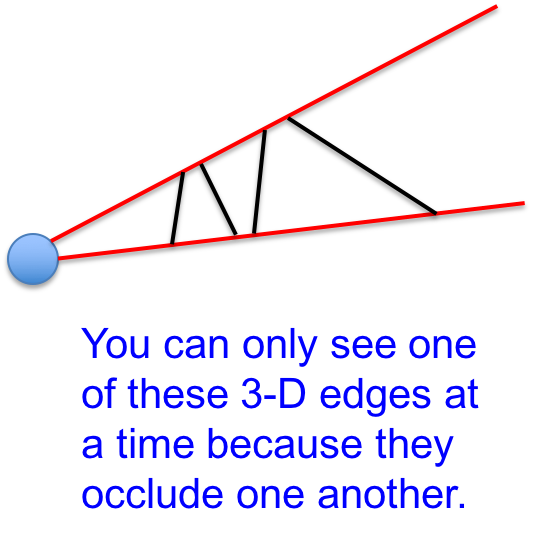
假设原点是眼球，红线是视界的边缘，那么所有的黑线在视网膜上的投影都是一模一样的。2D图像上的线条丢失了3D世界中的深度信息，对2D图像中的一条线来讲，存在着许多对应的3D边缘。

2D到3D的例子

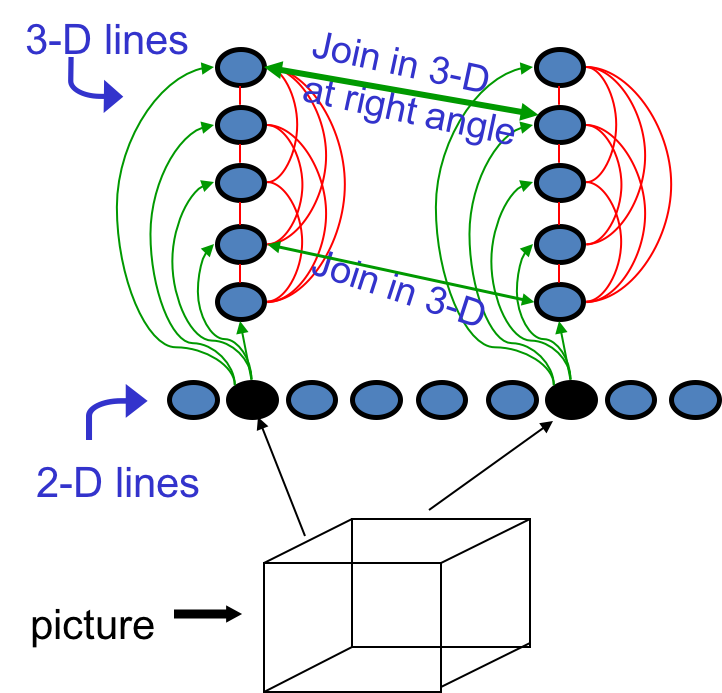
从下往上看，网络接受了一个2D奈克方块。其中两条边分别激活了两个输入单元，这就是输入数据。由于每条2D线条实际上对应了3D世界中的许多边缘，所以每个输入单元激活了许多隐藏单元（绿线所示）。但实际上只有一条3D边缘是真实的，所以这些隐藏单元必须彼此竞争，只留一个（红线所示）。3D世界中的边缘有交点，对奈克方块来讲，可能是：

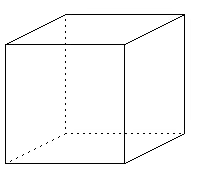
也可能是：

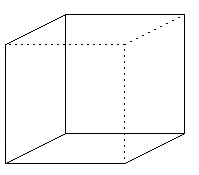
所以隐藏单元中有两条弧分别表示这两种交汇方式，粗细的不同表示支持这种可能性的大小。

关于奈克方块，援引wiki上有趣的背景知识：

奈克方块是个有歧义性的图，一种诠释方式是在一个较高位置看透明立方体的俯视图，另一种诠释方式是在一个较低位置看透明立方体的仰视图。

人类的视觉系统在接收这类的图像时，会设法诠释图像的各部分，使整体的图像没有矛盾之处。有时会用奈克方块来测试人人类视觉系统的电脑模型，测试电脑模型是否可以像人类视觉系统一様的诠释这个图象。

大多数的人在看奈克方块时，会将左前方的面视为立方体最接近观察者的一面，也许是因为人们在物体上方俯视物体的概率远高于物体下方仰视物体的情形，因此大脑倾向以这个的方式来诠释图像。

人类在观看奈克方块时，不会对方块的各部分有不一致的诠释。若有不一致的诠释，其结果可能会类似不可能立方体，是不可能物体的一种。

由奈克方块可以看出人类视觉系统的一些特性。人类诠释奈克方块的方式可以说明人脑有类似类神经网络的特性，存在二个不一様，但都可以互换的稳定状态[2]。西德尼·布拉德福在出生后10个月就失明，在52岁时接受手术恢复视力，他观看奈克方块时不会像一般人有模棱两可诠释的情形。

 知识共享署名-非商业性使用-相同方式共享：码农场 » Hinton神经网络公开课11 Hopfield nets and Boltzmann machines