Hinton神经网络公开课12 Restricted Boltzmann machines (RBMs)

终于到了玻尔兹曼机的训练了，这种简单的模型拥有优雅的理论基础，训练起来却又慢又差，曾一度被认为不实用。这节课讲解几种高效的学习算法，以及RBM应用到协同过滤的例子。

学习目标

这是种无监督学习，只有输入向量的参与。我们想要最大化训练集中的二值向量被玻尔兹曼机赋予的概率之积，当然，一般用概率对数之和。这也等价于，无输入情况下让网络稳定到stationary distribution N次，每次采样一次visible vector；如此能够“回忆起”这N个输入向量的概率。

为何学习很困难

考虑如下链式单元：

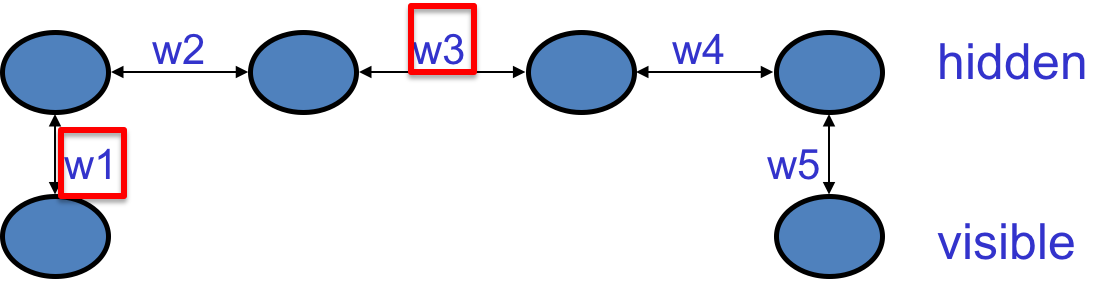
2个可见单元，4个隐藏单元。

如果训练集是$(1,0)$和$(0,1)$，则所有权值之积必须是负的。如果是正的，则第一个可见节点被激活的时候，第二个也倾向于激活……最后一个可见节点也会被激活。而如果权值中仅有一个是负数的话，则会使两个可见单元状态“相反”。

这说明，在训练的时候，一个权值需要知道其他权值是什么。比如$w_1$需要知道关于$w_3$的信息，两者进行的更新是相反的。

惊人的事实

上述权值彼此“依赖”的性质带来了一种只需要局部信息的训练算法:

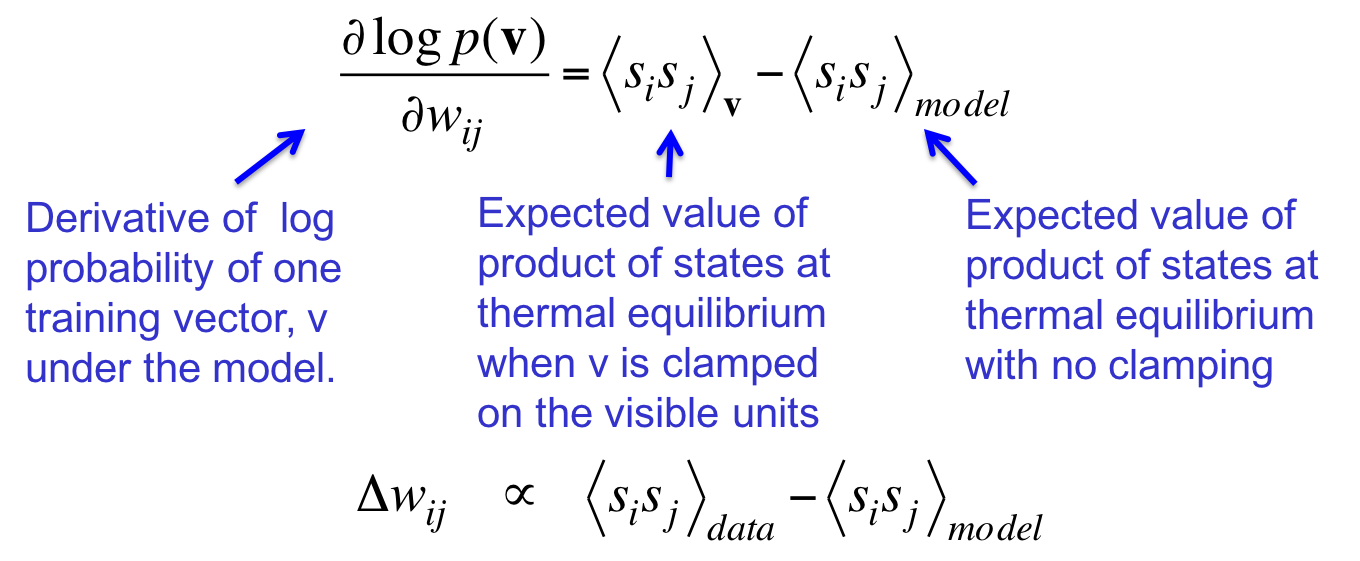
一个权值只需要知道这两个值就知道如何更新自己。在thermal equilibrium 状态下，其一是限定可见单元是$v$时两端状态乘积的期望，其二是不限制时两端状态乘积的期望。前者又称data，鼓励给定数据后按照激活值的大小增大权值，这是Hebbian learning rule的最简形式。该rule称大脑突触可能遵从这样的规则。但如果只遵从这个rule的话，突触的强度只会越来越大。所以需要第二项来平衡一下。第二项指的是这两个单元同时on的概率。

更准确的理解方式是，把第一项看作是Hopfield net的容量，第二项看作是去掉spurious minima（unlearning的精确值）。

为何导数如此简单

在thermal equilibrium 状态下，一组global configuration的概率是能量的指数函数。所以概率的对数就是能量的线性函数，这是个对数线性模型。于是有：

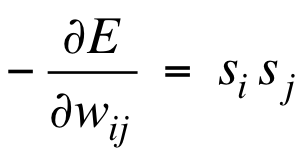
系统进入thermal equilibrium状态的过程实际上仅仅是传播关于权值的信息，而无关“数据”“误差”的信息；这一点与反向传播显著不同。

为何需要第二项

那个带负号的第二项存在理由是什么呢？

刚才简单地说了第二项看作是去掉spurious minima（unlearning的精确值），现在详细地解释一下。

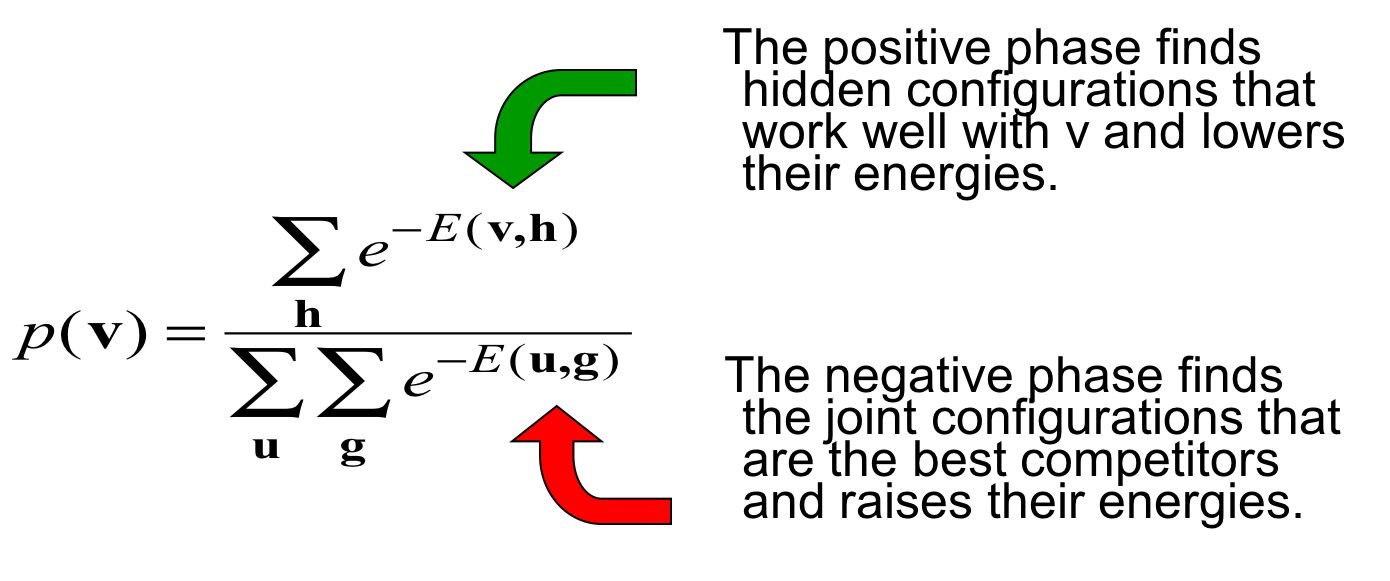
第一项对应分子，是正的，也就是要增加分子、降低$(v,h)$对应的能量；第二项对应分母，是负的，也就是要减小分母、增大竞争者（spurious minima）的能量。

一种效率低的训练方式

训练时需要得到两个统计信息：在用数据中的向量进行clamp可见单元的时候，收集的positive statistics；以及不提供数据、unlearning时的negative statistics。具体说来

• Positive phase：将可见单元固定为数据向量，将隐藏单元设为随机状态。每次更新一个隐藏单元，直到达到温度为1的thermal equilibrium 。对每个相连的pair，统计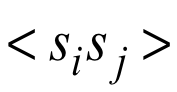。在整个数据集上重复此过程，并平均上述采样到的频次。

• Negative phase：与Positive phase类似，只不过不固定可见单元，而是将所有单元都设置为随机状态。

更加高效的方法

这一节的知识比较高级，如果不感兴趣可以跳过。

更好的统计方法

上面讲的原始方法的弱点是，如果从随机初始状态起步，则需要耗费很长时间才能抵达thermal equilibrium，也不容易判断究竟抵达了没有。更聪明的方法是将抵达thermal equilibrium时的状态与此时的data vector缓存下来，下来遇到一样的data vector时，直接从缓存的状态起步。这些缓存的状态被称作particle。

这有点像“热启动”，其原理是，如果我们只略微修改了一点权值，则应该只需要额外的少量步骤就能重返thermal equilibrium。

Neal’s method 

具体的做法是：

• Positive phase：缓存一组data-specific particles，串行地更新每个particle中的某个隐藏单元，之后将相连且为on的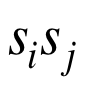在所有的particle上取平均。

• Negative phase：缓存一组fantasy particles，每个particle都是一组global configuration。串行地更新所有单元，取平均。

更新公式依然为。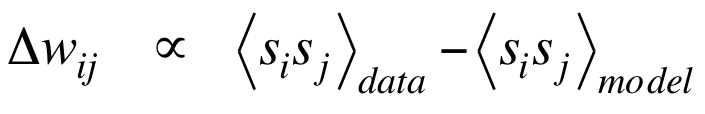

这种做法在full-batch上的效果更好。

让Neal方法适配mini-batch

在mini-batch上效果不好的原因是，mini-batch轮转了几个轮回。下次看到data vector的时候，权值发生了太多改变，particle中缓存的configuration已经离thermal equilibrium太远了。

解决方法是做一个关于人类认知世界的强假设（有点知识论的味道）：

当固定了data vector的时候，假设一个模型永远只会给出同一个表达。也就是说即使有些模型可以给出多个好的表达，但我们限制自己只寻找那些只给出一个表达的模型。

simple mean field approximation 

在这种假设下，我们可以使用一种叫做simple mean field approximation 的高效算法。

为了符合统计，隐藏单元必须串行地按照如下概率更新：

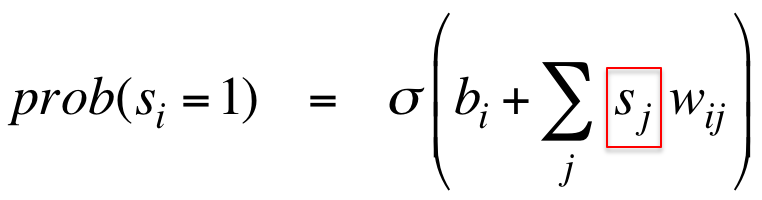
红框中的$s_j$也是个随机的二值单元，这决定了串行化。

为了并行化，我们可以将$s_j$替换为随机的0到1之间的实值（也是一个概率）：

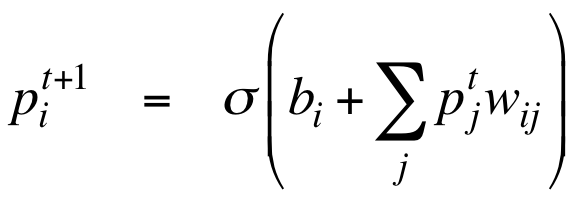
两者并不是等效的，因为被替换的部分位于非线性的逻辑斯谛函数中，而不是线性函数中。虽然理论上解释不通，但实践效果很好。哪怕并行化更新带来了一些震荡，也可以通过damped mean field来缓解：

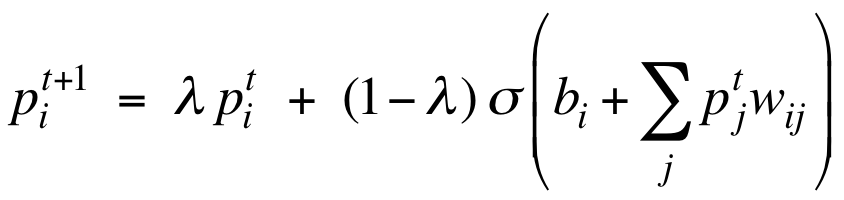
这个改进的公式有点平滑的意味。

高效的玻尔兹曼机mini-batch学习算法

于是得到了一种适配mini-batch的高效算法：

• Positive phase：将所有隐藏单元的概率初始化为0.5。然后可见单元设置为data vector；使用damped mean field方法并行更新隐藏单元直到收敛（概率不发生变化）；收敛后记录每个pair的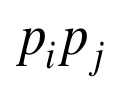，在所有mini-batch上平均。

• Negative phase：（与Neal方法相同）缓存一组fantasy particles，每个particle都是一组global configuration。串行地更新所有单元，取平均。

进一步并行化

注意到上一小节的Negative phase并没有得到并行化，如果要并行化这部分，则可以改变玻尔兹曼机的架构：

• 去掉同一个层内的连接

• 不允许跨层的连接

• 允许多个隐藏层

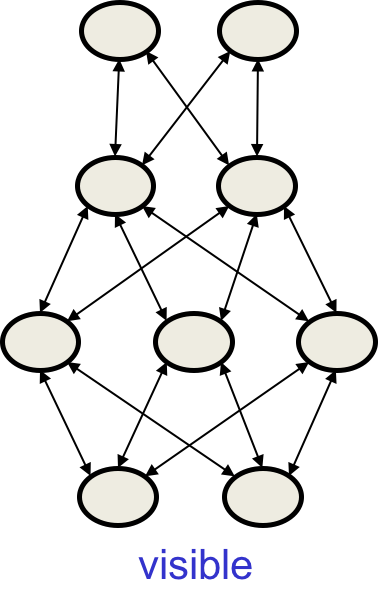
这被称作Deep Boltzmann Machine (DBM)，本质上是缺失了很多连接的玻尔兹曼机的泛化形式。

虽然我们无法同时更新所有相连的单元，但我们可以只更新其中一端。由于存在很多层，所以每次可以更新一半的节点：

DBM能够胜任处理MNIST吗

一个评价方法是，看看DBM生成的数据是否接近真实数据。试验证明，的确很像：

右边是真实数据，左边是DBM虚构的。

谜题

试验中只使用了100个negative examples ，怎么能刻画所有可能的configuration呢？configuration space是极度高维的，才100个例子足够吗？

训练提高了effective mixing rate

我暂时不清楚此处的mixing是什么意思，大致的思路是，当fantasy particles的数量比positive data多的时候，该处的能量上升。这使得fantasy particles离开局部最低点，进入下一个最低点。所以fantasy particles的数量少点也行，人少多干活儿就是了。

 知识共享署名-非商业性使用-相同方式共享：码农场 » Hinton神经网络公开课12 Restricted Boltzmann machines (RBMs)