目录
![]()
![]()
![]()
![]()
![]() 这次课比较轻松,先回顾反向传播的历史,探讨其在90年代遭到冷落的原因。然后过渡到概率图模型,讲了Deep Belief Net及其与RBM的异同、训练算法等。
这次课比较轻松,先回顾反向传播的历史,探讨其在90年代遭到冷落的原因。然后过渡到概率图模型,讲了Deep Belief Net及其与RBM的异同、训练算法等。
反向传播简史
这个著名的算法在70和80年代被重复发明多次:
-
Bryson & Ho (1969) linear
-
Werbos (1974)
-
Rumelhart et. al. in 1981
-
Parker (1985)
-
LeCun (1985)
-
Rumelhart et. al. (1985)
反向传播给了人们训练多层非线性feature detectors的承诺,但在发明之初并没有很好地兑现这个承诺。于是在90年代,正统的机器学习学者们放弃了它。在诸如心理学和工业界领域,它还有应用;但在机器学习领域,它已经被支持向量机替代了。
反向传播失败的原因
流传最广的误解是:
-
反向传播无法利用多层和非线性的特征(除了CNN之外)
-
它也无法用来训练RNN和deep auto-encoders(后面会覆盖),而RNN恰恰是最令人激动的模型
-
SVM效果更好、需要更少的专业知识、能产生可复现的结果、并且有更fancy的理论
但真实原因是:
-
计算机比最低要求慢了几千倍
-
标注数据集比最低要求小了几百倍
-
当时的深度网络太小了,并且初始化得很粗糙,经常是稍微深一点的网络梯度就消失了
这些原因导致了反向传播的失利。
统计学与人工智能的区别
| 统计学 | 人工智能 |
| 数据纬度低(100以内) | 高维数据(高于100) |
| 数据中有许多噪音 | 噪音不算事 |
| 数据没有多少结构,可以被简单模型捕捉 | 数据有大量结构,复杂到简单模型无法捕捉 |
| 主要课题是将数据的规律与噪音分离开(不适合非高斯神经网络,适合SVM或高斯过程) | 主要课题是找到复杂结构的恰当表示,以使其可被学习(手工特征模板或最好用反向传播) |
为什么SVM不适合需要好的知识表示的人工智能任务
有两种观点:
SVM只不过是高配的感知机。SVM多了个核技巧,将输入拓展为一个非常大的非线性non-adaptive(非自适应,也就是手工确定)特征层,这个特征表示不用学习。SVM只学习这一层到决策单元的权值,过人之处是用上了间隔最大化的策略来防止过拟合。
另一种观点还是认为SVM只不过是高配的感知机。但这种观点对特征变换的认识不同,认为SVM将训练集中的每个输入向量映射为一个non-adaptive的特征,预测时实际上在为测试输入向量匹配一个训练输入向量。之后SVM使用了聪明的方法同时进行特征选择和一层的权值学习。
两种观点是非常类似的,那就是SVM本质上是单层的高配感知机,无法学习多层的特征表示。
神经网络vs SVM的赌局

J赌到2000年,人们将从理论上弄明白为什么神经网络在大规模数据集上效果不那么坏;但如果作为SVM领头者的V证明了神经网络的限制和条件,那也算V赢了。而V赌到了2005年根本没人会像1995年那样使用神经网络。
事实证明两者都输了,到了现在人们还在像以前那样使用神经网络,但神经网络的限制不是理论不好,而是计算力不够。
Belief Nets
这一节介绍Belief Nets。当时标注数据集非常小,Hinton放弃了反向传播又想应用梯度下降法。生成式模型是个好主意,因为目标函数是为输入数据建模而不是预测标签。其中概率图模型利用独立的图结构来表示变量之间的依赖关系,于是可以通过一些变量的观测值预测某个变量的概率。
玻尔兹曼机实际上是图模型的早期例子,只不过是无向图而已。1992年Radford Neal指出,利用玻尔兹曼机中的单元和有向边,则得到一种称作“Sigmoid Belief Nets”的图模型。这时候,又要关心学习算法了。
反向传播的问题
-
需要标注数据,可是几乎所有数据都是未标注的
-
训练时间很长,特别是深层网络(初始化得不好)
-
可能会卡在局部最优,一般网络上还凑合,但深度网络中离全局最优相差甚远。是否有一种凸函数的模型呢?数学家很喜欢这个主意,但这类模型在实际应用中复杂度远低于真实数据
通过无监督学习克服反向传播的限制
这种方法是,保留梯度方法的高效与简洁性,但是应用到捕捉输入的结构上。也就是说,不再捕捉输入到输出的映射规律,而是通过调整权值来最大化生成输出的概率。举例来讲,要实现计算机视觉,先要让模型学会计算机图形学(画画)。
生成式模型的学习目标是最大化p(x) 而不是 p(y | x)。这时候就有两个分支了:
-
类似于玻尔兹曼机那样的基于能量的模型
-
由理想化的神经元构成的因果模型(先看看这种)
-
或者两者的结合体(最后学习这种)
人工智能与概率
先来了解一下背景知识。老爷子说在70-80年代,那时候他还是个研究生。人工智能领域是忌谈概率的,如果你讨论概率,那就说明你还没入门。计算机处理的是离散信号,而不是连续的概率。第一部AI教科书如此写道:
许多古希腊人支持苏格拉底“深层复杂的思想来自神”的观点。这种观点中“神”在现代的代言人是不稳定的甚至概率论的神经元。增加神经元的随机性更可能带来癫痫病和酒疯,而不是智能的进步。
但早在1958年,富有远见卓识的John von Neumann曾在生前的《The Computer and the Brain》手稿中预言,一种新的计算机系统将远离传统的形式逻辑,而接近热力学系统。如果Neumann再活得久一点,也许人工智能领域会是另一番繁荣的面貌。
图论和概率论的联姻
80年代的许多AI系统都是专家系统,使用一堆规则来处理诊断或寻矿的问题。但学者们依然很讨厌概率,哪怕要处理不确定性,他们也不愿意应用概率。
概率论学家终于通过图模型的途径进入了AI领域。
-
图模型擅长表达“什么依赖什么”
-
于是在给定其他节点的状态时需要利用概率来计算某个节点
Belief Nets是一种稀疏连接的,有向无环图模型。在此之上发明了聪明的推断算法。由于算法复杂度是相连节点数目的指数函数,所以在稠密连接图模型上很低效。
Belief Nets
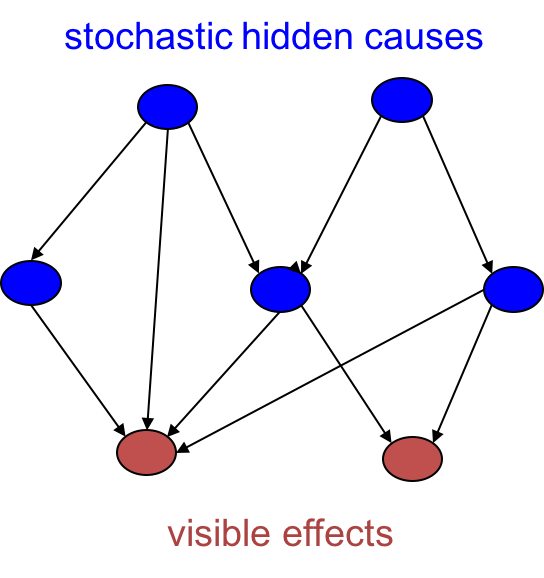
这是一种由随机变量组成的有向无环图,其中隐藏单元作为原因引起叶子单元的发生。一旦我们观测到一些叶子单元的取值,有两个问题需要解决:
-
推断问题:推断隐藏变量(概率分布),如果隐藏变量彼此依赖,则会非常非常复杂
-
学习问题:给定一组叶子单元的取值,如何调整隐藏单元的相互作用以使得网络生成该数据集的概率最大。
图模型与神经网络
早期的图模型依靠专家手工定义图结构以及其中的条件概率,当时的图是非常稀疏的。由于知识来自专家,所以学者们并不关注训练方法。
而神经网络中人肉特征则从来都是下品的做法。知识来自对数据的学习,网络结构并不倾向于可解释性或为了使推断简单而增加稀疏性。然而,的确存在神经网络版本的Belief Net。
两种由随机二值神经元构成的生成式神经网络
-
基于能量的模型:对称连接多个随机二值神经元得到玻尔兹曼机。添加一些限制,得到更容易学习的RBM。但是这些模型只能有一个隐藏层,失去了多层神经网络的威力。
-
因果模型:由随机二值单元构成的有向无环图,或称Sigmoid Belief Net (Neal验证了该模型比玻尔兹曼机稍微容易训练一些)
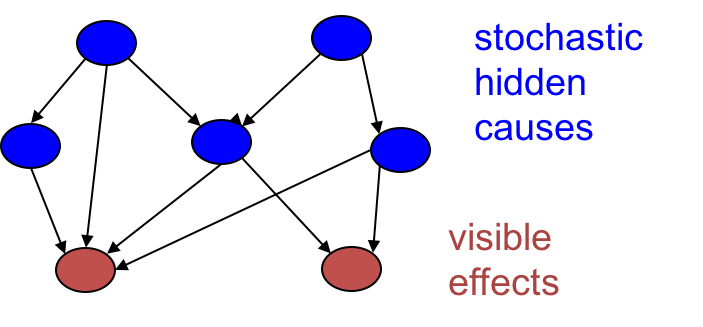
在Sigmoid Belief Net中,从上到下根据上一层的激活值、权值和这一层的偏置随机决定这一层的激活值,一直递推到可见单元。这种生成样本的机制比玻尔兹曼机要简单得多。
![]() 知识共享署名-非商业性使用-相同方式共享:码农场 » Hinton神经网络公开课13 Stacking RBMs to make Deep Belief Nets
知识共享署名-非商业性使用-相同方式共享:码农场 » Hinton神经网络公开课13 Stacking RBMs to make Deep Belief Nets
 码农场
码农场