码农场目录
Learning Sigmoid Belief Nets
这一节介绍训练Sigmoid Belief Nets的难处，以及两种训练方法。不同于玻尔兹曼机训练的两个过程，Sigmoid Belief Nets只需要positive phase。这是因为Sigmoid Belief Nets是一种locally normalized model，于是就不需要处理partition function及其导数。如果给定可见单元的数据向量，能够很容易地从隐藏单元的后验分布无偏置采样的话，就可以利用最大似然来学习参数了。然而获取后验概率分布并采样并不容易，这是由于一种称为“explaining away”的现象。
训练完成后，很容易根据网络的参数生成叶子单元上的无偏置样本。由于因果模型自顶而下的结构，这太简单了。
但是给定可见单元，则很难推断隐藏单元的后验概率分布。这是因为隐藏单元状态数是节点数的指数函数。就算有了后验概率分布，也难以采样一个样本出来。
Sigmoid Belief Nets的learning rule
先不考虑如何采样，假设给定观测数据能够很简单地从后验概率分布中采样一个样本的话，学习会变得很简单。假设$s_j$是从后验概率分布上采样到的全局configuration，则对每个下级单元i来讲，只需要最大化所有上级单元推断该单元的概率对数。这个learning rule是local（无关其他被推断节点、无全局归一化）而简单的。
计算公式如下：
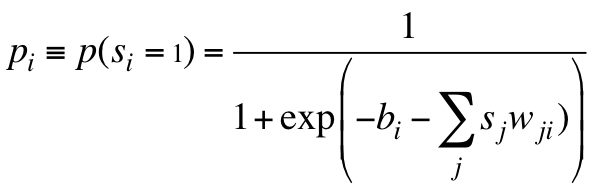
学习算法需要最大化这个概率，则需要如下更新父节点到被推断的节点的权值：
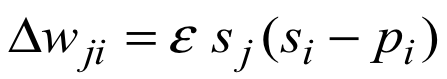
为何难以从后验概率分布采样（Explaining away ）
考虑如下的简单Sigmoid Belief Net，其中有两个隐藏单元（原因）和一个可见单元（结果）：
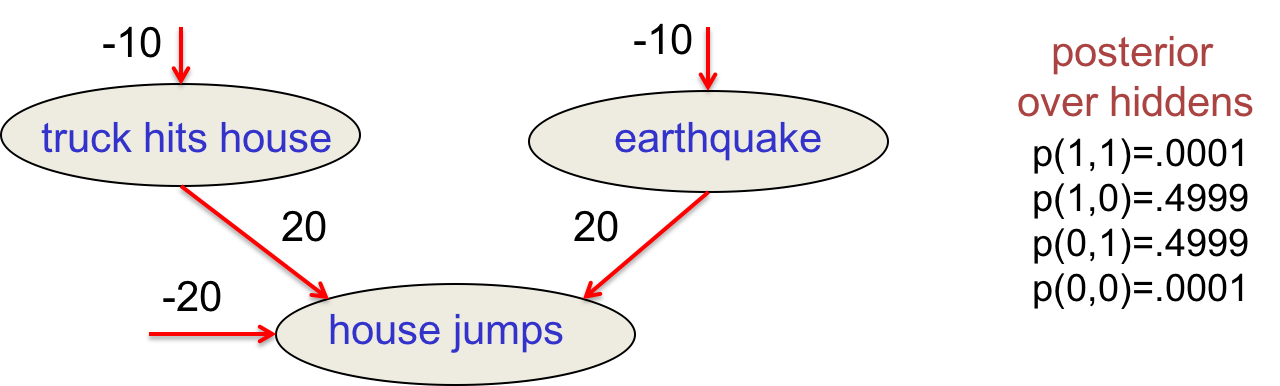
这里房子震动的偏置非常大，除非两个原因中有且仅有一个为真，则几乎不可能发生。如果其中只有一个发生了，代入上述$p_i$公式，20与20抵消，房子会以$\frac{1}{2}$的概率震动。
由图可知，卡车撞墙和地震的概率都是$e^{-10}$，于是两者发生一个时房子震动的概率是$\frac{1}2e^{-10}$。而两者同时发生时房子震动的概率则为$\frac{1}2e^{-20}$，即便观测到房子震动了，这也非常不可能。
这个例子说明地震会降低卡车撞墙导致房子震动的概率，在房子震动的时候，两个因素是相互抵触的。而事实上，在模型的先验中，这两个因素是完全独立的。
后验概率如上图所示，两种configuration非常不可能出现，另外两种则很可能出现；很可能出现的两种恰好是隐藏节点相反的情况。这种看上去隐藏节点相关性很高而实际上不高的现象就叫做Explaining away。
为何Sigmoid Belief Net学习难
回到原先的问题上来，考虑如下网络：
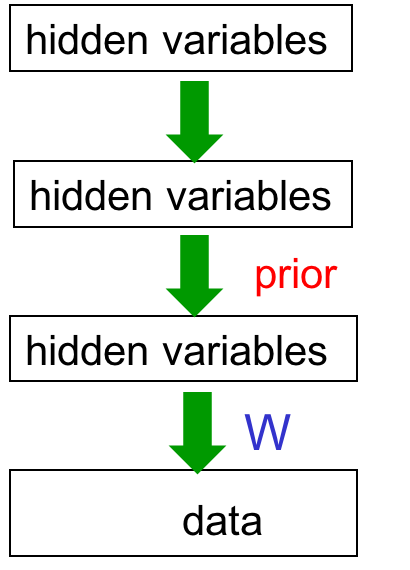
从上往下数，假设要学习倒数第一层到可见单元的权值W，则需要先得到这一层的先验。而这一层的随机变量的先验概率将因Explaining away而不再是独立的阶乘的形式，反而是相关的。要得到先验概率，需要遍历所有的configuration，由于指数级的复杂度，根本没法实现。另外后验概率取决于先验，也取决于最大似然。我们还需要知道其他隐藏层的权值，导致了所有的权值相互联系，无法单独更新。
一些训练方法
-
Monte Carlo methods
考虑所有父节点、祖父节点……的configuration，运行马尔科夫链到“热量均衡”状态，采样。但对大型深度网络来讲，还是太慢了。 -
variational methods
这种方法放弃了获取无偏置的样本，而是从近似后验概率的其他分部分布获取近似的样本。 -
近似概率分布有什么保证吗？
有的，可以保证是原后验概率的对数的下界。通过提高下界，通常可以提高后验概率。
The wake-sleep algorithm
这是一种有效的训练方法，虽然有两个phase，但切不可与玻尔兹曼机的学习算法搞混了，因为该算法是面向有向图模型的。其背后的思想还开辟了机器学习的新领域——variational learning。
其基本思想是用计算廉价的分布代替真实分布，然后假装采样的样本来自真实分布去做最大似然。算法里面有两项，一项尽量地拟合数据，另一项尽量地调整真实后验概率来拟合计算廉价的分布。
一个看上去疯狂的主意
总结一下，学习类似Sigmoid Belief Nets的复杂模型很难。难点在于给定datavector，难以估计所有隐藏单元上的后验概率分布，连从该分布采样都非常难。
疯狂的主意：从其他分布采样，寄希望于训练依然有效。这种替代的分布能够忽略explaining away。详细地说，就是假设每一层的隐藏节点之间都是独立的，有点像RBM。于是后验概率就可以被分解为一个个独立的乘法项了。
Factorial distributions
在这种分布中，整个向量的分布是每个元素的概率之乘积。假设三个隐藏单元激活的概率如下：
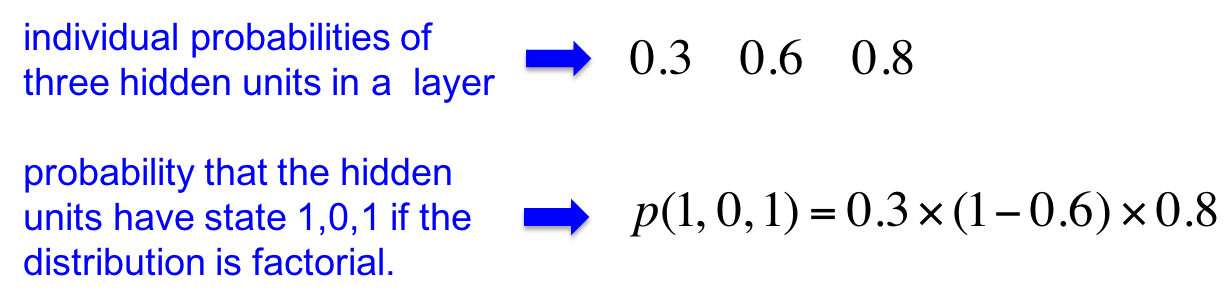
则向量$(1,0,1)$的概率只是三个项的乘积。
一般分布下的N元向量的自由度(degrees of freedom)是$2^N$（准确值是$2^N-1$，因为要让概率之和为1）。但Factorial distribution的自由度为N（我的理解是，对任意元素，只要确定了$p_i$就确定这一维度的分布）。
wake-sleep算法
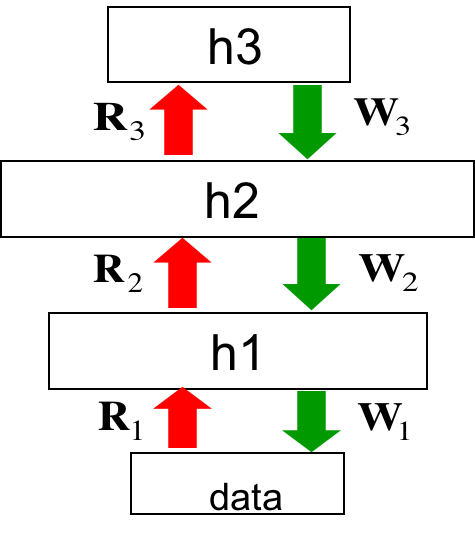
有两种weight，绿色是神经网络因果模型中的weight，而红色则是用来模拟正式后验概率分布的Factorial distribution的weight，称作recognition weights。有两个phase：
Wake phase：使用recognition weights来执行自底而上的推断（前向传播）。也就是在每一个隐藏层对每个隐藏单元做出独立的随机决策它是否被激活。在此之后，将这个激活值的configuration当作正式后验概率分布下的一个采样。利用这个采样进行最大似然，自顶而下训练generative weights。
Sleep phase：与Wake phase相反，从随机vector开始，自顶而下根据generative weights激活单元，直到生成数据。这个过程中生成的样本是无偏置的。利用这些样本自底而上训练recognition weights，让其从数据恢复隐藏状态。
轮换两个phase，可以训练出非常棒的模型。
算法的缺陷
-
算法初期模型生成的数据偏离真实数据非常远，却被用来训练recognition weights。这很浪费，但不是大问题。
-
大问题是recognition weights不服从数据的概率对数的梯度，也不严格服从这个概率的variational bound 的梯度。这将导致错误的mode-averaging。
-
最后的问题是最顶层的隐藏层中的单元由于explaining away效果是非常不独立的，而我们在用独立的Factorial distribution去模拟它。这对中间的隐藏层可能还不那么明显，因为下面来的explaining away效果可能幸运地被上面来的先验抵消。
-
无论如何，Karl Friston 认为这是大脑的工作方式。但Hinton老爷子现在觉得这个算法还是问题太多了，大脑应该有更好的算法。
Mode averaging
这一小节利用上面见过的房子震动例子来解释Mode averaging。
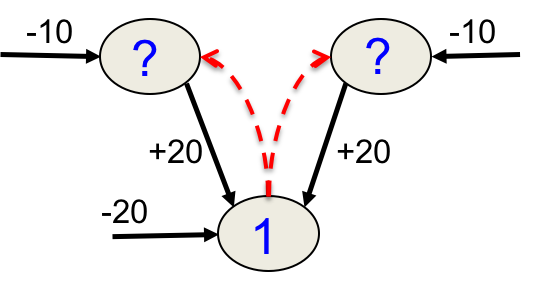
假设运行sleep phase去生成数据。大部分时间两个隐藏单元都是off状态，这是由它们的先验决定（地震和卡车撞墙概率很小）。由于两者是off的，所以可见单元也是off的，因为它的偏置是$-20$。
假设以$e^{-10}$的概率偶发了一次两个隐藏单元中的一个被激活了，一旦激活了，可见单元的激活概率为$\frac{1}{2}$。想象一下可见单元激活的情况中，有一半是左边的隐藏单元激活，另一半是右边的，几乎没有其他情况。
那么recognition weights会怎样地更新呢？给定data为on，recognition weights会学着为两个隐藏单元产生$(0.5,0.5)$的factorial分布。这个分布却把一半的概率放到了(1,1)和(0,0)上去（红色），而这两者是非常不可能的configuration。
真正最佳的factorial分布是只挑一个隐藏单元激活，并给它全部概率密度（绿色）。
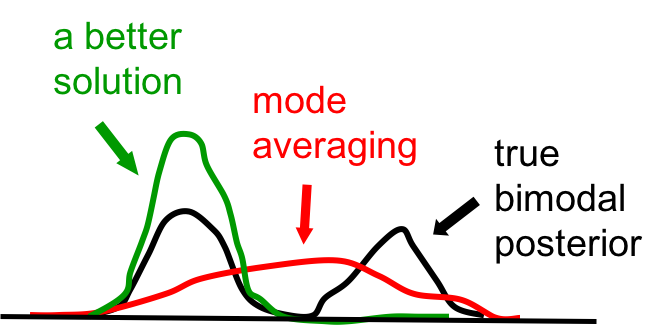
黑色是真实分布，红色是将概率均分给四种configuration的factorial distribution，绿色在最理想的factorial distribution。因为算法是在操纵真实分布来拟合factorial distribution，而不是反过来。
知识共享署名-非商业性使用-相同方式共享：码农场 » Hinton神经网络公开课13 Stacking RBMs to make Deep Belief Nets