目录
两个计算难题
用隐藏单元来表示输入的interpretation时,有两个问题要解决。
-
搜索(这节课讲):如何防止被困在局部能量最低点
-
学习(下节课讲):如何学习隐藏单元之间的连接权值
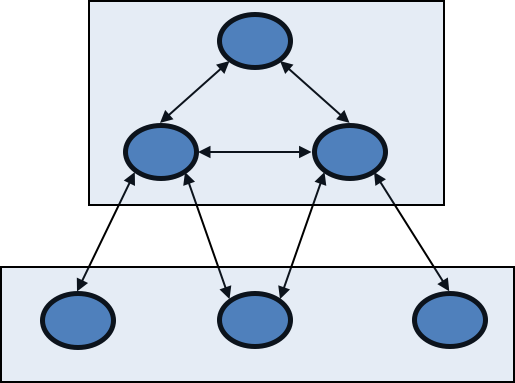
利用随机单元改善搜索
这一节介绍利用噪音来“逃离”局部最低点。
Hopfield net永远都根据是否能够减小能量来贪婪地下决策,导致无法脱离局部最低点。
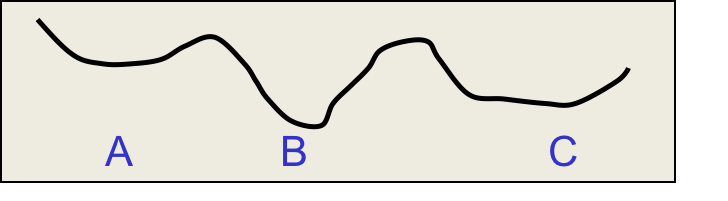
上面这张能量图谱中,在局部最低点A,无法到达全局最低点B,因为有一段能量上升的坡。加上噪声,则能够越过一些不那么陡峭的坡。可以以较多的噪音起步,探索一个区域,然后降低噪音,稳定到较低的能量状态。这种方法被称作“simulated annealing”。
温度对转移概率的影响
在一个物理系统,或一个由能量函数决定的系统中,高温度会使能量图谱变得平坦。举例来讲,

高能量相对提高了从B到A的概率,降低了从A到B的概率。此时跨越能势变得更容易,但也更容易离开能量最低点。
在温度较低的系统中,转移概率普遍减小,但低能量转移到高能量的概率相对下降得更显著:

相应地状态更容易停留在能量最低点。
这验证了刚才讲的“以较多噪音起步”的方法。
随机二值单元
在网络中引入噪音的具体做法是,将binary threshold units替换为二值随机单元。“温度”控制噪音的量,增多噪音相当于降低所有状态之间的能隙。
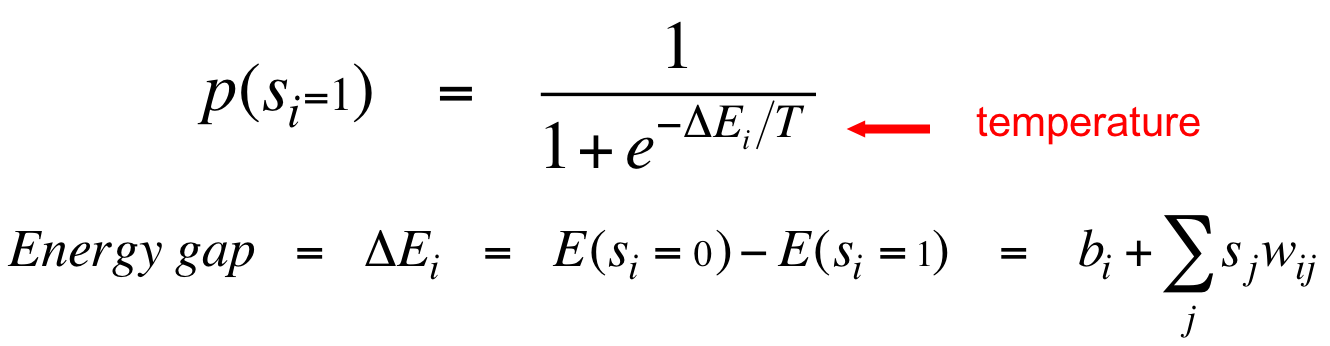
上面的逻辑斯谛方程分母中,能隙被温度缩放。当温度很高的时候,$p(s_i=1)=\frac{1}{1+e^0}=\frac{1}{2}$,单元将等概率随机地激活与关闭。温度降低,根据$\Delta{E}$的符号,概率或大或小。而当温度为绝对零度的时候,随机二值单元退化为binary threshold units,也就是根据能隙$\Delta{E}$的符号或者一定输出0,或者一定输出1。
事实上Simulated annealing启发了Boltzmann machines,但又偏离了Boltzmann machines,这门课不会深入讲。
接下来假定温度为1。
热量均衡
这是个复杂的概念,均衡并不意味这系统处于能量最低的静止状态,而是系统状态的概率分布稳定下来。这种分布被称作stationary distribution,此时每种状态的概率与其能量函数的相反数成正比。可以这样想想,假设许多系统有相同的能量函数,一个系统configuration(状态)的概率就是那些拥有此状态的系统所占的比例。
逼近热量均衡
要达到热量均衡,只需按任意分布生成不同configuration的系统,甚至可以任选一个configuration然后说其概率为1。然后对每个configuration中的每个单元应用stochastic update rule ,也就是随机挑一个单元,根据其能隙得到概率随机决定激活还是关闭它。如此运行一段时间后,每种configuration的比例趋于稳定,也就达到了物理学家所说的热量均衡状态。
一个类比
假设在拉斯维加斯赌场有许多荷官(远大于$52!$个)在洗牌,假设洗牌之前都是一样的顺序。洗了几次之后,有可能大王还是紧挨着小王。但洗了很长时间之后,所有$52!$种顺序都将等可能地出现,此时就达到了热量均衡。让所有荷官再洗一次,那么离开某状态的牌与进入某状态的牌的数量将会是一致的。
这个类比唯一不恰当的地方是所有的排序能量相同,这是导致它们等可能的原因。
Boltzmann Machine
这一节介绍玻尔兹曼机是如何为一系列二值向量建模的。讲解将从“为什么要处理二值向量”开始,逐步过渡到模型的应用。
处理二值数据
带有随机隐藏单元的Stochastic Hopfield nets又被称作Boltzmann Machine(玻尔兹曼机),擅长处理二值数据。给定一组二值向量作为训练数据,玻尔兹曼机能够拟合数据并给出任意一个二值向量的概率。
这种二值向量可能来自文档的特征向量,用于文本分类。也可能用于复杂系统的异常检测,比如核电站,此时不太可能用监督学习,因为没有监督数据。也可能用于计算不同分布的模型产生某个观测数据的概率:
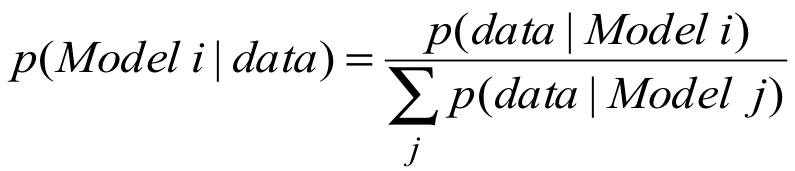
因果模型如何产生数据
在因果模型中,数据由下列两个步骤产生:
-
根据先验分布挑选隐状态
-
根据给定隐状态的条件分布挑选显状态
在神经网络生成式因果模型中,条件分布概率由hidden到visible的权值和偏置体现:
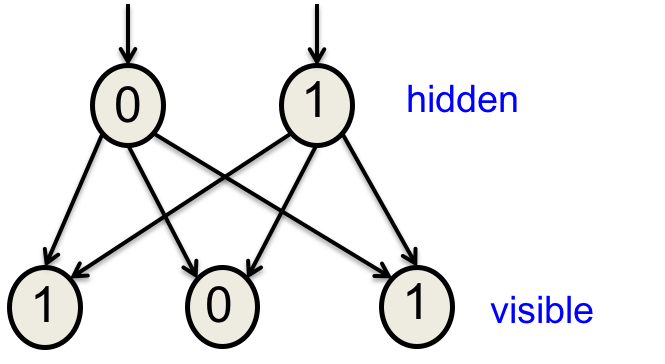
生成某个显状态向量的概率是所有可能的隐状态生成该显状态的概率之和。每个隐状态都是该向量的一种“解释”。
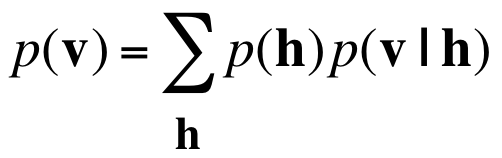
这是最常见的一种生成式模型,也符合人的认知。以至于一提起生成式模型,人们首先想到的就是因果模型。
玻尔兹曼机如何生成数据
但玻尔兹曼机则是另外一种流派,它是基于能量的。隐状态和显状态的joint configuration概率由能量决定,这种决定方式体现在下列两种方式:
-
可以简单地把联合分布定义为:
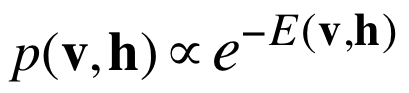
-
也可以“迭代式”地定义两者的联合概率为,更新网络的随机二值单元许多次后得到的网络状态的概率
幸运的是,两种定义方式实际上是一致的。
joint configuration的能量
完整的能量方程如下:
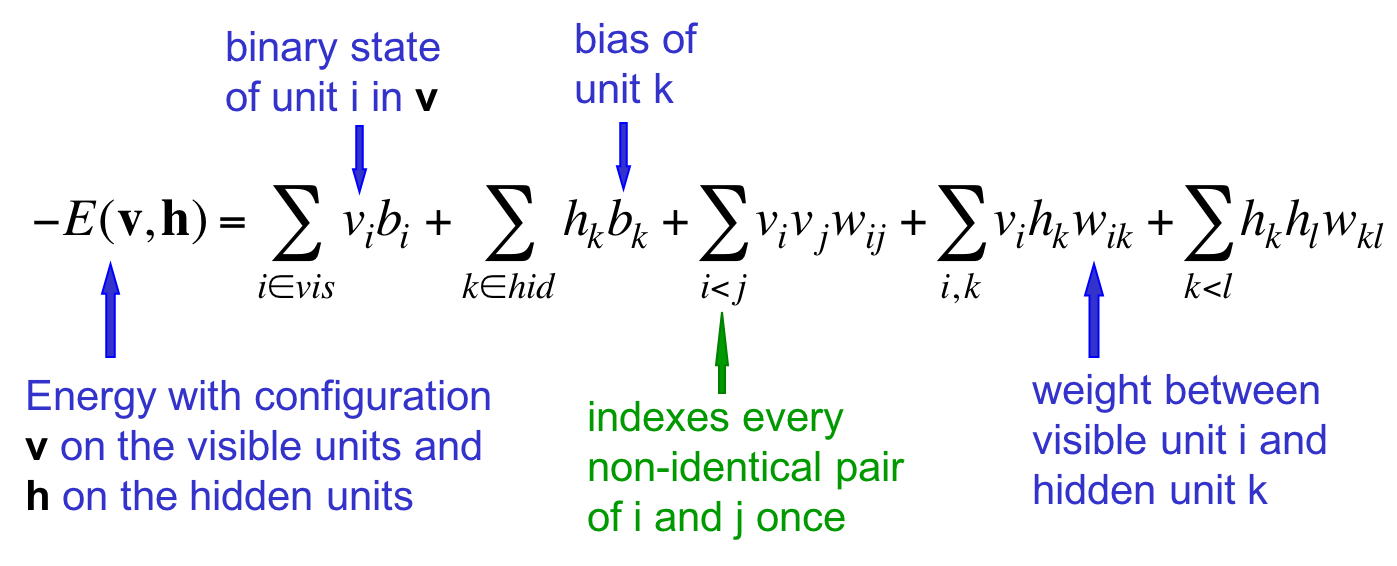
看上去有点复杂,其实很简单。v表示可见单元,h表示隐藏单元,它们都是二值的。求和时约束$i<j$是为了防止重复计算一个pair两次。
使用能量决定概率
一个joint configuration的概率是其能量比上所有configuration能量之和:
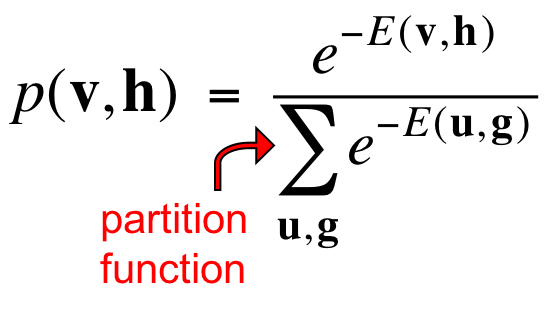
分母的作用是归一化,物理学家称其为partition function。
而某个可见单元的configuration的概率是,含有该可见单元configuration的所有联合configuration的能量之和所占的比例:
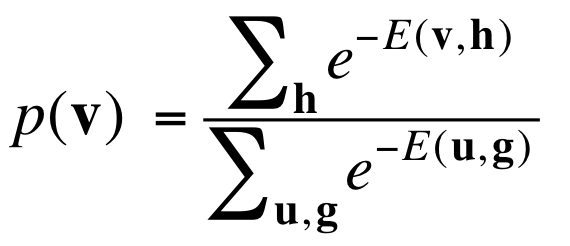
举个例子
虽然公式也不难,但举例说明理解更好。在下列简单的网络中:
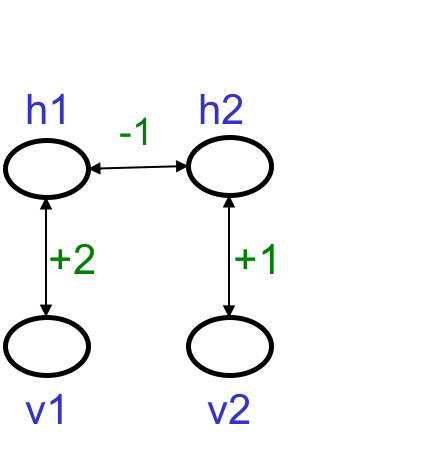
一共两个隐藏单元,两个可见单元,无偏置。
从做到右,写下所有可能的隐藏configuration,及其对应的所有可能的可见configuration,计算负能量,计算联合概率,求和得到可见configuration的概率:
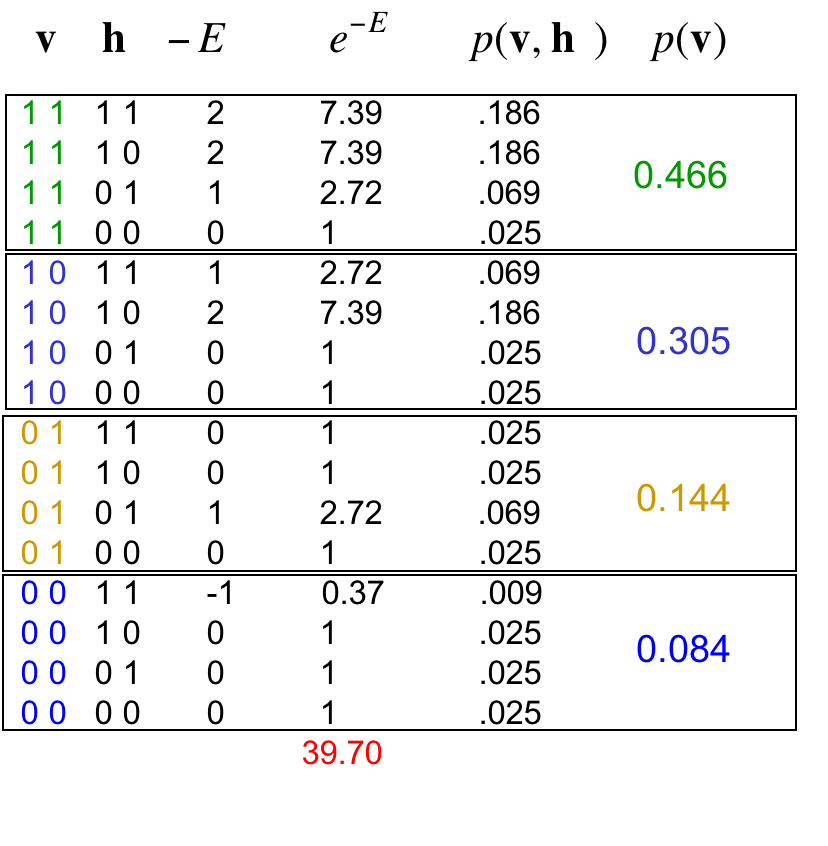
从模型中采样
如果模型的隐藏单元特别多,则不可能算出归一化项,因为项数是指数级增长的。于是利用上节课介绍的Markov Chain Monte Carlo法,先随机取一个configuration,然后不停地挑选单元让其根据能隙随机更新状态直到马尔科夫链使其达到热量均衡状态。此时某个configuration的概率由其能量与玻尔兹曼分布决定:
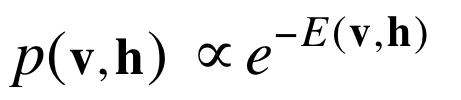
给定数据向量,从隐藏configuration上的后验概率分布采样
有时候我们想要训练模型,有时候我们想得到一个数据在玻尔兹曼机上的表达,这时候就需要根据后验概率分布采样了。
做法与上一小节类似,由于所有可能的隐藏configuration数量是指数级增长的,所以需要Markov Chain Monte Carlo法从后验概率分布中采样。只不过实施的时候,可见单元的configuration与数据向量保持一致,而只允许更新隐藏单元的状态。
![]() 知识共享署名-非商业性使用-相同方式共享:码农场 » Hinton神经网络公开课11 Hopfield nets and Boltzmann machines
知识共享署名-非商业性使用-相同方式共享:码农场 » Hinton神经网络公开课11 Hopfield nets and Boltzmann machines
 码农场
码农场
哇 我还是从国际经济法那里来的,是同一个学姐吗?好厉害啊