这次练习在USPS手写邮政编码数据集上训练识别模型,重点是训练神经网络时的各种调参技巧。
数据集
数据全集有11000张图片,其中1000作为训练集,1000作为验证集,9000作为测试集(训练集与测试集的比例不同寻常,很容易过拟合,富有挑战性)。
输入维度为256:
>> size(data.training.inputs) ans = 256 1000
每一维都是0到1之前的浮点数。
代码
大部分代码都写好了,加载数据集、执行优化、显示结果。唯一需要完成的损失函数的梯度函数。
定义
快速把代码框架过一遍。
class FFNeuralNet: """Implements Feedforward Neural Network from Assignment 3 trained with Backpropagation. """ def __init__(self, training_iters, validation_data, wd_coeff=None, lr_net=0.02, n_hid=300, n_classes=10, n_input_units=256, train_momentum=0.9, mini_batch_size=100, early_stopping=False): """Initialize neural network. Args: training_iters (int) : number of training iterations validation_data (dict) : contains 'inputs' and 'targets' data matrices wd_coeff (float) : weight decay coefficient lr_net (float) : learning rate for neural net classifier n_hid (int) : number of hidden units n_classes (int) : number of classes train_momentum (float) : momentum used in training mini_batch_size (int) : size of training batches early_stopping (bool) : saves model at validation error minimum """ self.n_classes = n_classes self.wd_coeff = wd_coeff self.batch_size = mini_batch_size self.lr_net = lr_net self.n_iterations = training_iters self.train_momentum = train_momentum self.early_stopping = early_stopping self.validation_data = validation_data # used for early stopping # model result params self.training_data_losses = [] self.validation_data_losses = [] # Model params # We don't use random initialization, for this assignment. This way, everybody will get the same results. self.n_params = (n_input_units + n_classes) * n_hid theta = np.transpose(np.column_stack(np.cos(range(self.n_params)))) * 0.1 if self.n_params else np.array([]) self.model = self.theta_to_model(theta) self.theta = self.model_to_theta(self.model) assert_array_equal(theta.flatten(), self.theta) self.momentum_speed = self.theta * 0.0
此处的
self.n_params = (n_input_units + n_classes) * n_hid
说明是一个全连接的网络,即所有输入单元连上了所有隐藏单元、所有隐藏单元连上了所有输出单元。
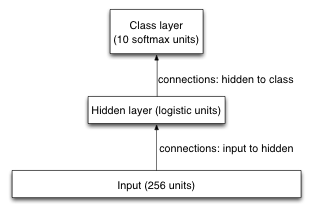
然后根据参数数量进行“伪随机初始化”:
theta = np.transpose(np.column_stack(np.cos(range(self.n_params)))) * 0.1 if self.n_params else np.array([])
这句实际上在按余弦生成固定数目的值:
cos(0:10) ans = 1.0000 0.5403 -0.4161 -0.9900 -0.6536 0.2837 0.9602 0.7539 -0.1455 -0.9111 -0.8391
得到的向量$\theta$就是模型的参数向量。
接下来有两个拼装和分解参数向量的静态方法:
@staticmethod
def model_to_theta(model):
"""Takes a model (or gradient in model form), and turns it into one long vector. See also theta_to_model."""
model_copy = copy.deepcopy(model)
return np.hstack((model_copy['inputToHid'].flatten(), model_copy['hidToClass'].flatten()))
@staticmethod
def theta_to_model(theta):
"""Takes a model (or gradient) in the form of one long vector (maybe produced by model_to_theta),
and restores it to the structure format, i.e. with fields .input_to_hid and .hid_to_class, both matrices.
"""
n_hid = np.size(theta, 0) / (NUM_INPUT_UNITS + NUM_CLASSES)
return {'inputToHid': np.reshape(theta[:NUM_INPUT_UNITS * n_hid], (n_hid, NUM_INPUT_UNITS)),
'hidToClass': np.reshape(theta[NUM_INPUT_UNITS * n_hid: np.size(theta, 0)], (NUM_CLASSES, n_hid))}
训练
def train(self, sequences):
"""Implements optimize(..) from assignment. This trains using gradient descent with momentum.
Args:
model_shape (tuple) : is the shape of the array of weights.
gradient_function : a function that takes parameters <model> and <data> and returns the gradient
(or approximate gradient in the case of CD-1) of the function that we're maximizing.
Note the contrast with the loss function that we saw in PA3, which we were minimizing.
The returned gradient is an array of the same shape as the provided <model> parameter.
Returns:
(numpy.array) : matrix of weights of the trained model (hid_to_class)
"""
self.reset_classifier()
if self.early_stopping:
best_so_far = dict()
best_so_far['theta'] = None
best_so_far['validationLoss'] = np.inf
best_so_far['afterNIters'] = None
n_training_cases = np.size(sequences['inputs'], 1)
for i in xrange(self.n_iterations):
training_batch_start = (i * self.batch_size) % n_training_cases
training_batch_x = sequences['inputs'][:, training_batch_start: training_batch_start + self.batch_size]
training_batch_y = sequences['targets'][:, training_batch_start: training_batch_start + self.batch_size]
self.fit(training_batch_x, training_batch_y)
self.momentum_speed = self.momentum_speed * self.train_momentum - self.gradient
self.theta += self.momentum_speed * self.lr_net
self.model = self.theta_to_model(self.theta)
self.training_data_losses += [self.loss(sequences)]
self.validation_data_losses += [self.loss(self.validation_data)]
if self.early_stopping and self.validation_data_losses[-1] < best_so_far['validationLoss']:
best_so_far['theta'] = copy.deepcopy(self.theta) # deepcopy avoids memory reference bug
best_so_far['validationLoss'] = self.validation_data_losses[-1]
best_so_far['afterNIters'] = i
if np.mod(i, round(self.n_iterations / float(self.n_classes))) == 0:
print 'After {0} optimization iterations, training data loss is {1}, and validation data ' \
'loss is {2}'.format(i, self.training_data_losses[-1], self.validation_data_losses[-1])
# check gradient again, this time with more typical parameters and with a different data size
if i == self.n_iterations:
print 'Now testing the gradient on just a mini-batch instead of the whole training set... '
training_batch = {'inputs': training_batch_x, 'targets': training_batch_y}
self.test_gradient(training_batch)
if self.early_stopping:
print 'Early stopping: validation loss was lowest after {0} iterations. ' \
'We chose the model that we had then.'.format(best_so_far['afterNIters'])
self.theta = copy.deepcopy(best_so_far['theta']) # deepcopy avoids memory reference bug
reset方法将模型重置为初始状态:
def reset_classifier(self): """Resets the model parameters. """ theta = np.transpose(np.column_stack(np.cos(range(self.n_params)))) * 0.1 if self.n_params else np.array([]) self.model = self.theta_to_model(theta) self.theta = self.model_to_theta(self.model) self.momentum_speed = self.theta * 0.0
fit方法计算损失函数的梯度:
def fit(self, X, y): """Fit a model using Classification gradient descent. """ self._d_loss_by_d_model(inputs=X, targets=y) return self
梯度计算
具体的计算实现如下:
def _d_loss_by_d_model(self, inputs, targets): """Compute derivative of loss. Args: data (dict): - 'inputs' is a matrix of size <number of inputs i.e. NUM_INPUT_UNITS> by <number of data cases> - 'targets' is a matrix of size <number of classes i.e. NUM_CLASSES> by <number of data cases> Returns: dict: The returned object is supposed to be exactly like parameter <model>, i.e. it has fields ret['inputToHid'] and ret['hidToClass']. However, the contents of those matrices are gradients (d loss by d model parameter), instead of model parameters. """ ret_model = dict() # First, feed forward the values, capture the weight input's (class_input and hid_input) and # activations (class_output and hid_output) at every layer. hid_input = np.dot(self.model['inputToHid'], inputs) hid_output = logistic(hid_input) class_input = np.dot(self.model['hidToClass'], hid_output) class_prob = np.exp(self.predict_log_proba(class_input)) # Now, back propagate. Compute the delta error (error_deriv) for the output layer (the third layer). error_deriv = class_prob - targets # Compute the gradient for the output layer across all training examples then divide # across the training set size for each weight gradient. hid_to_output_weights_gradient = np.dot(hid_output, error_deriv.T) / float(np.size(hid_output, axis=1)) ret_model['hidToClass'] = hid_to_output_weights_gradient.T # Compute the delta error (backpropagate_error_deriv) for the hidden layer. backpropagate_error_deriv = np.dot(self.model['hidToClass'].T, error_deriv) # Compute the gradient for the hidden layer across all training examples then divide # across the training set size for each weight gradient. input_to_hidden_weights_gradient = np.dot(inputs, ((1.0 - hid_output) * hid_output * backpropagate_error_deriv).T) / float(np.size(hid_output, axis=1)) ret_model['inputToHid'] = input_to_hidden_weights_gradient.T # Add in the weight decay. ret_model['inputToHid'] += self.model['inputToHid'] * self.wd_coeff ret_model['hidToClass'] += self.model['hidToClass'] * self.wd_coeff self.gradient = self.model_to_theta(ret_model)
前四句前向传播,其中
def predict_log_proba(self, class_input): """Predicts log probability of each class given class inputs Notes: * log(sum(exp of class_input)) is what we subtract to get properly normalized log class probabilities. Args: class_input (numpy.array) : probability of each class (see predict_sequences_proba(..)) (size: <1> by <number of data cases>) Returns: (numpy.array) : log probability of each class. """ class_normalizer = log_sum_exp_over_rows(class_input) return class_input - np.tile(class_normalizer, (np.size(class_input, 0), 1))
计算的是softmax层输出的概率(或称假设$h_{\theta}(x)$)的对数:
$\begin{align}
h_\theta(x) =
\begin{bmatrix}
P(y = 1 | x; \theta) \\
P(y = 2 | x; \theta) \\
\vdots \\
P(y = K | x; \theta)
\end{bmatrix}
=
\frac{1}{ \sum_{j=1}^{K}{\exp(\theta^{(j)\top} x) }}
\begin{bmatrix}
\exp(\theta^{(1)\top} x ) \\
\exp(\theta^{(2)\top} x ) \\
\vdots \\
\exp(\theta^{(K)\top} x ) \\
\end{bmatrix}
\end{align}$
损失函数中误差的部分是:
$\begin{align}
J(\theta) &= - \left[ \sum_{i=1}^m (1-y^{(i)}) \log (1-h_\theta(x^{(i)})) + y^{(i)} \log h_\theta(x^{(i)}) \right] \\
&= - \left[ \sum_{i=1}^{m} \sum_{k=0}^{1} 1\left\{y^{(i)} = k\right\} \log P(y^{(i)} = k | x^{(i)} ; \theta) \right]
\end{align}$
导数之类的看http://www.hankcs.com/ml/programming-exercise-2-logistic-regression-cs229.html 吧,老生常谈了。
动量法
梯度有了,将历史速度乘以动量,减去梯度,乘以学习率应用到权值上去。注意这里的动量法与斯坦福系的稍有不同:http://www.hankcs.com/ml/sgd-cnn.html#h3-2 。
self.momentum_speed = self.momentum_speed * self.train_momentum - self.gradient self.theta += self.momentum_speed * self.lr_net self.model = self.theta_to_model(self.theta)
调节超参数
学习率
以较小学习率训练70个迭代,效果如下:
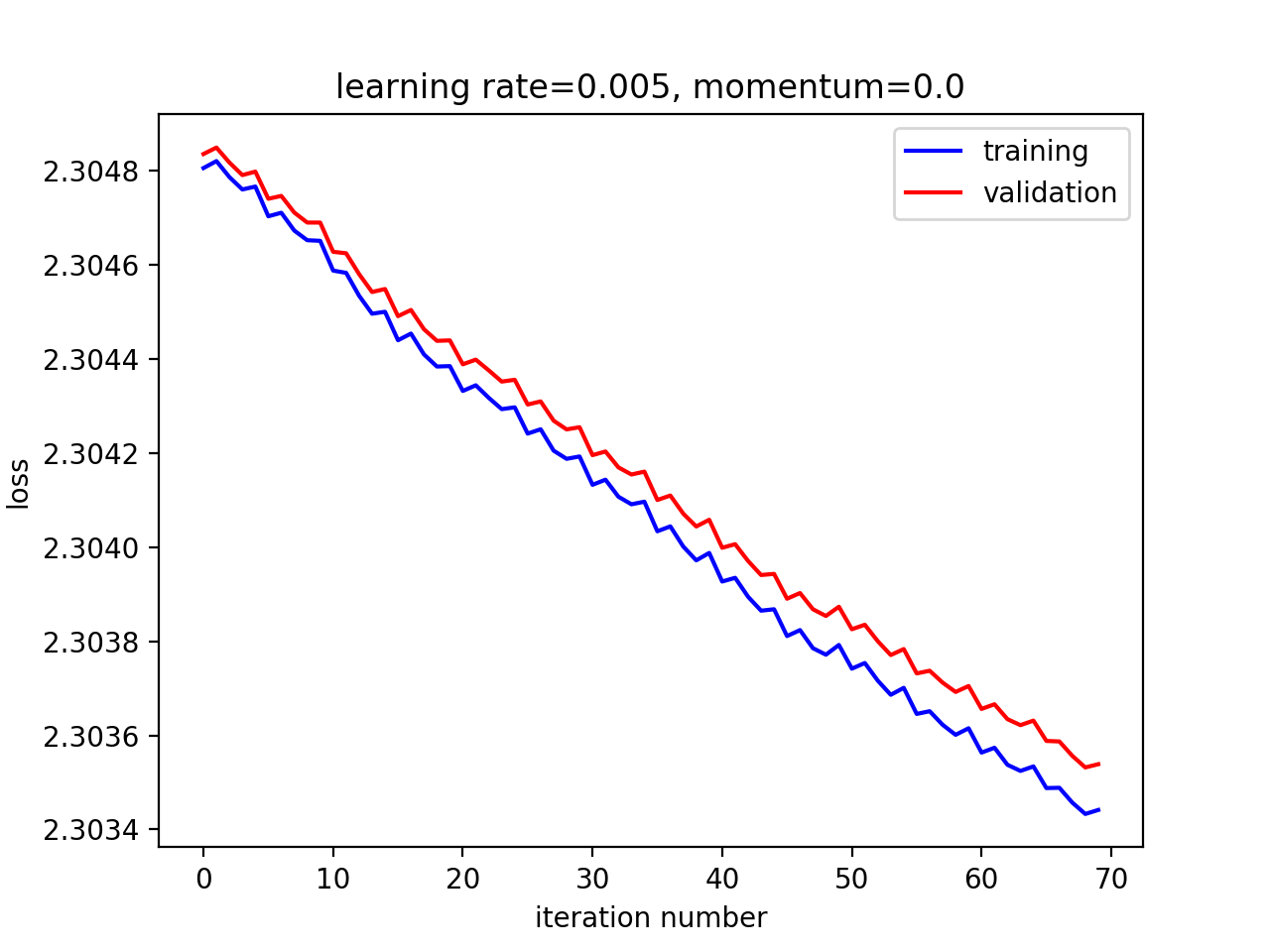
在学习率特别小的情况下,70个迭代做不了多少优化。我们可以训练更多迭代,但这样会容易过拟合。
试试大一点的学习率:
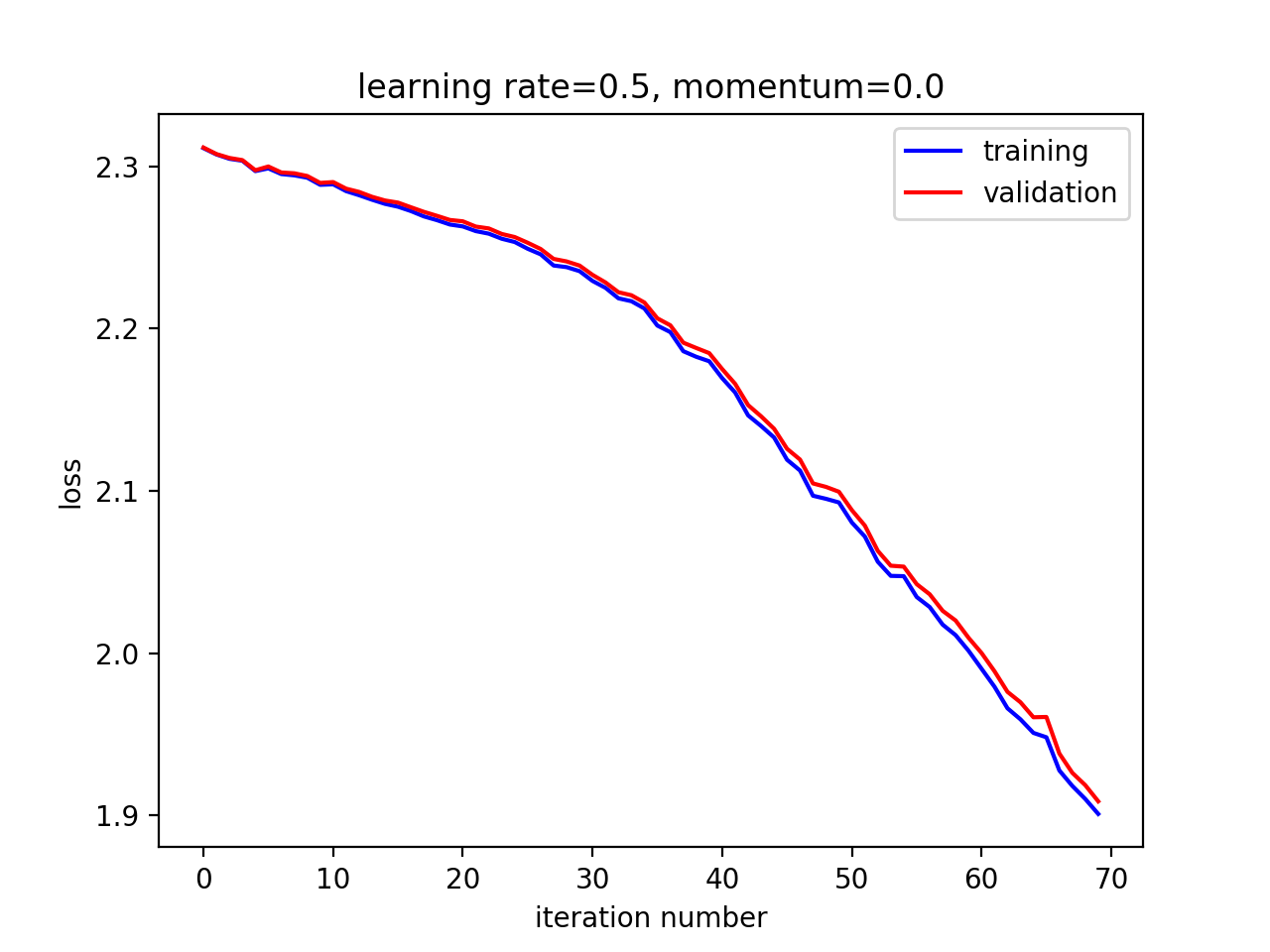
的确达到了更好的效果。
动量
如果加上动量,来个自动寻参:
learning_rates = [0.002, 0.01, 0.05, 0.2, 1.0, 5.0, 20.0]
momentums = [0.0, 0.9]
for momentum in momentums:
for learning_rate in learning_rates:
print "Momentum and learning rate are ({0}, {1})".format(momentum, learning_rate)
a3.a3_main(0, n_hid=10, n_iterations=70, lr_net=learning_rate, train_momentum=momentum,
early_stopping=False, mini_batch_size=4)
print
观察在不同超参数组合下的收敛速度与最终效果
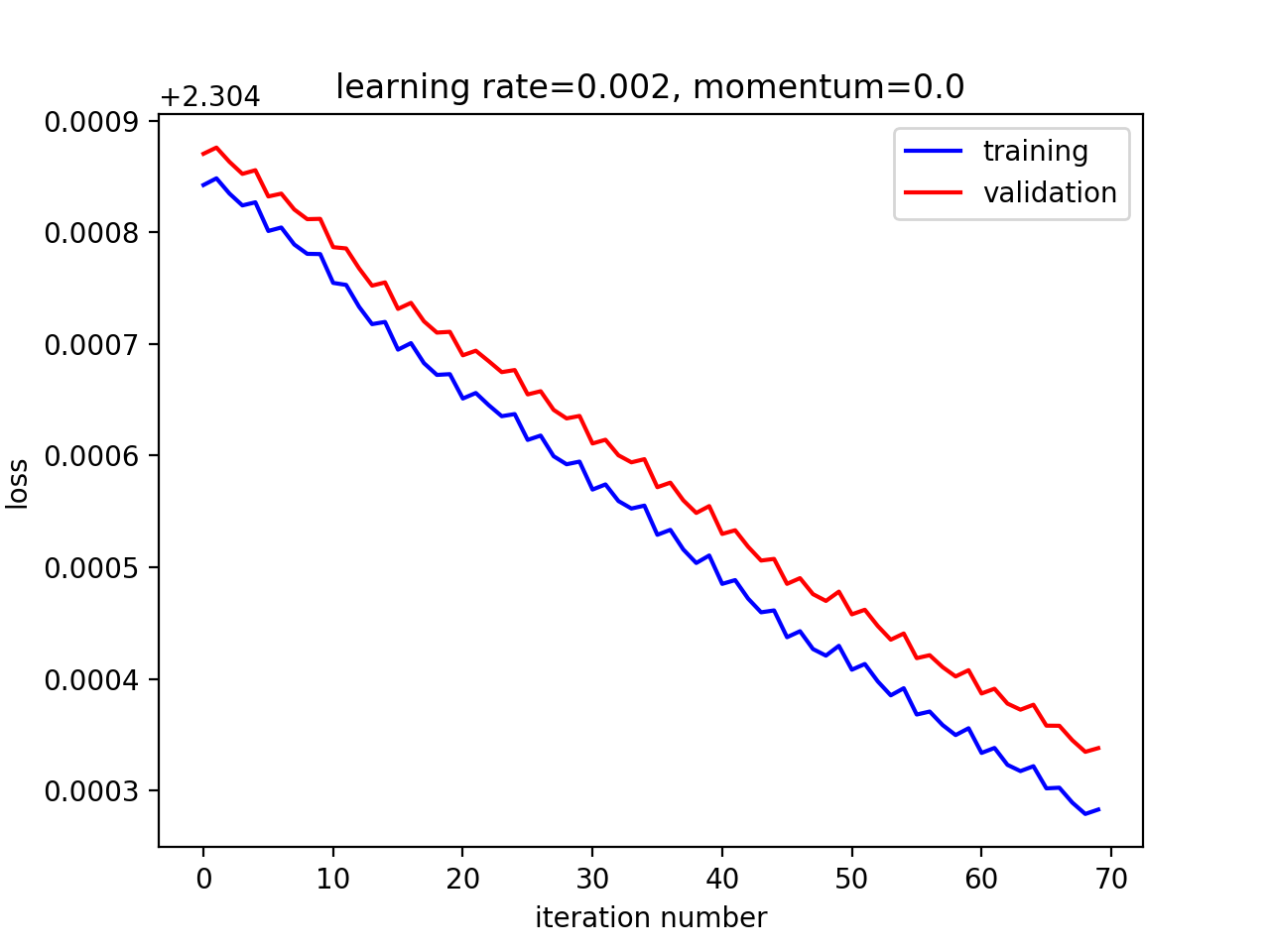
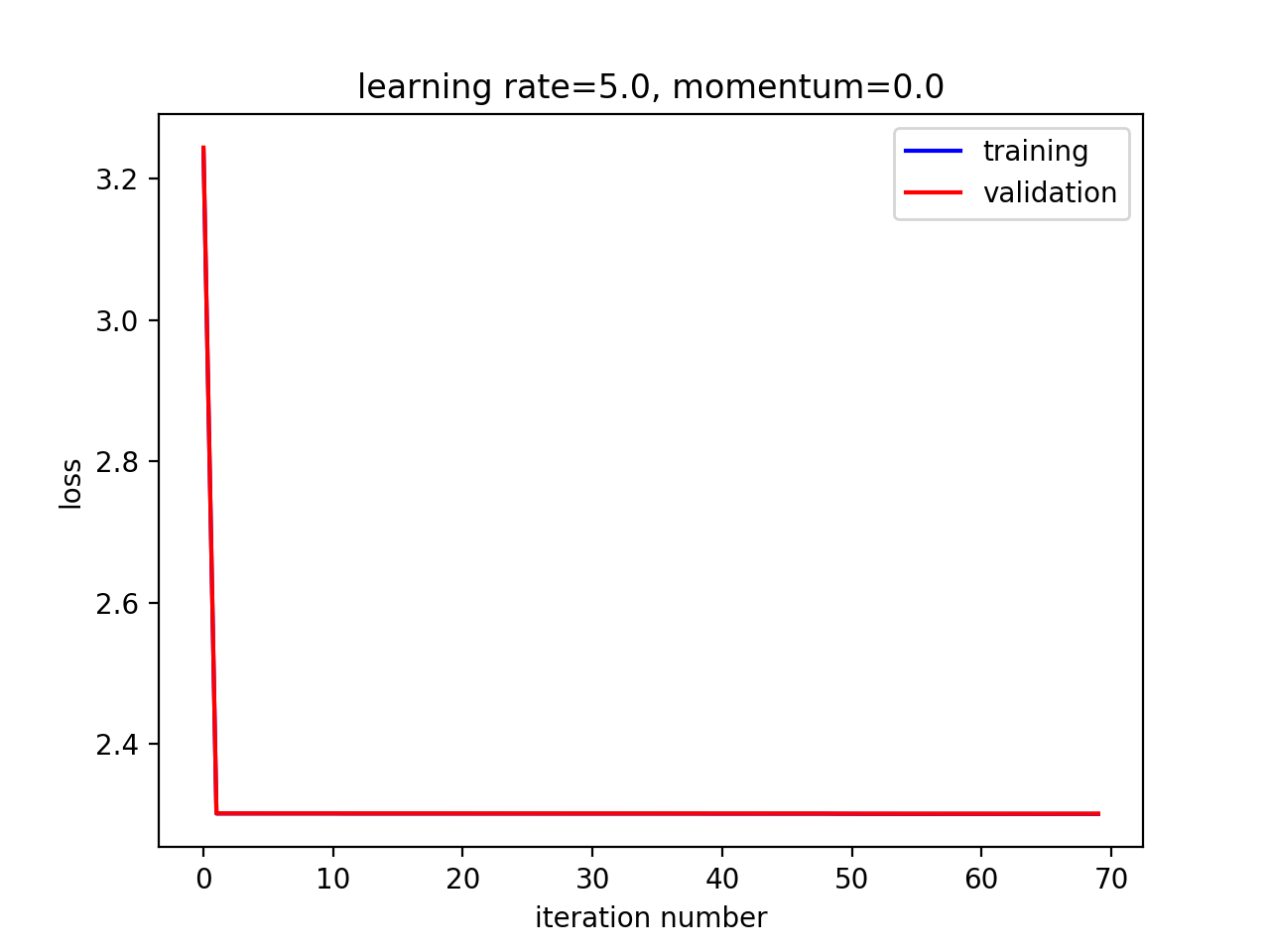
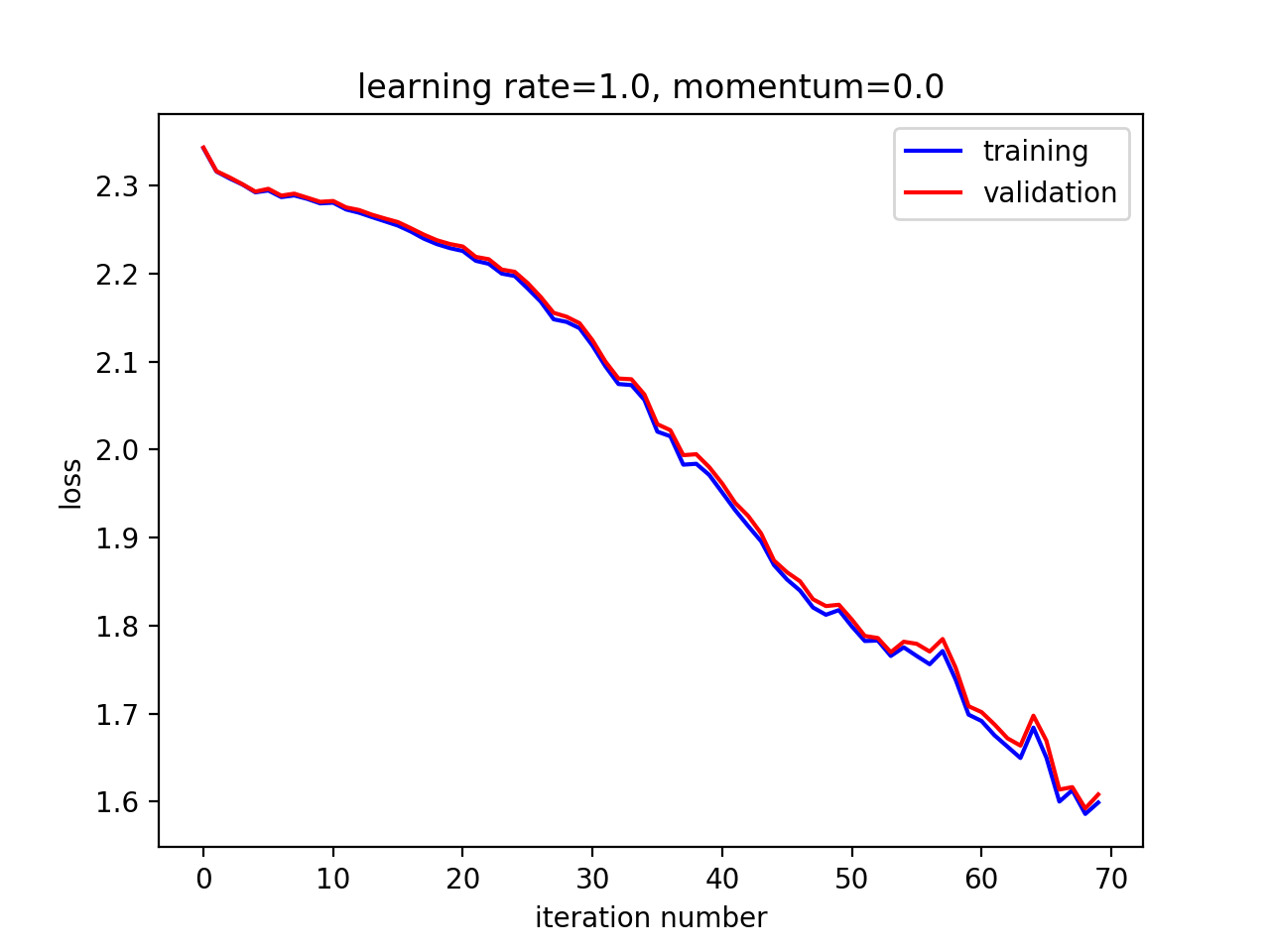
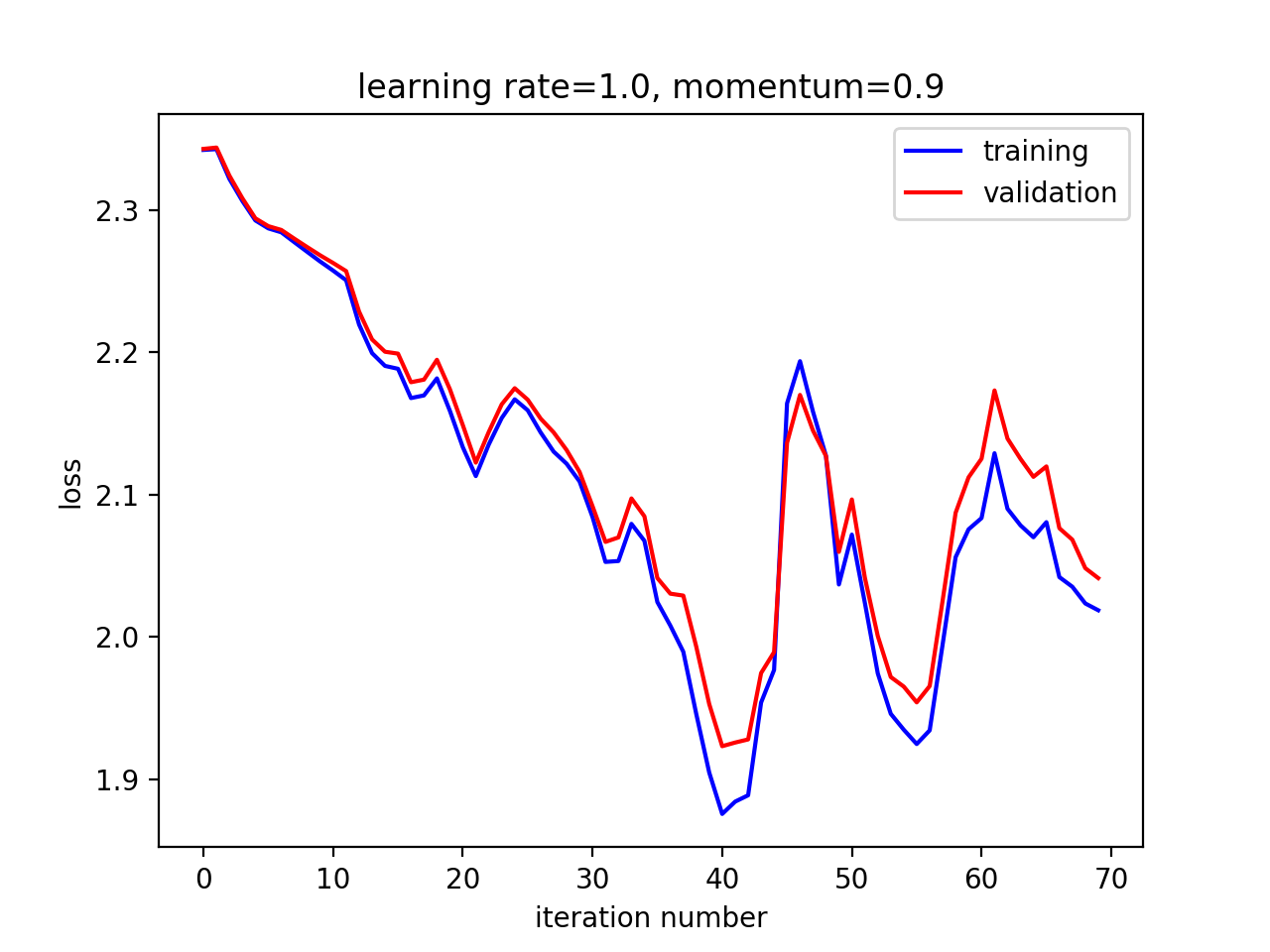
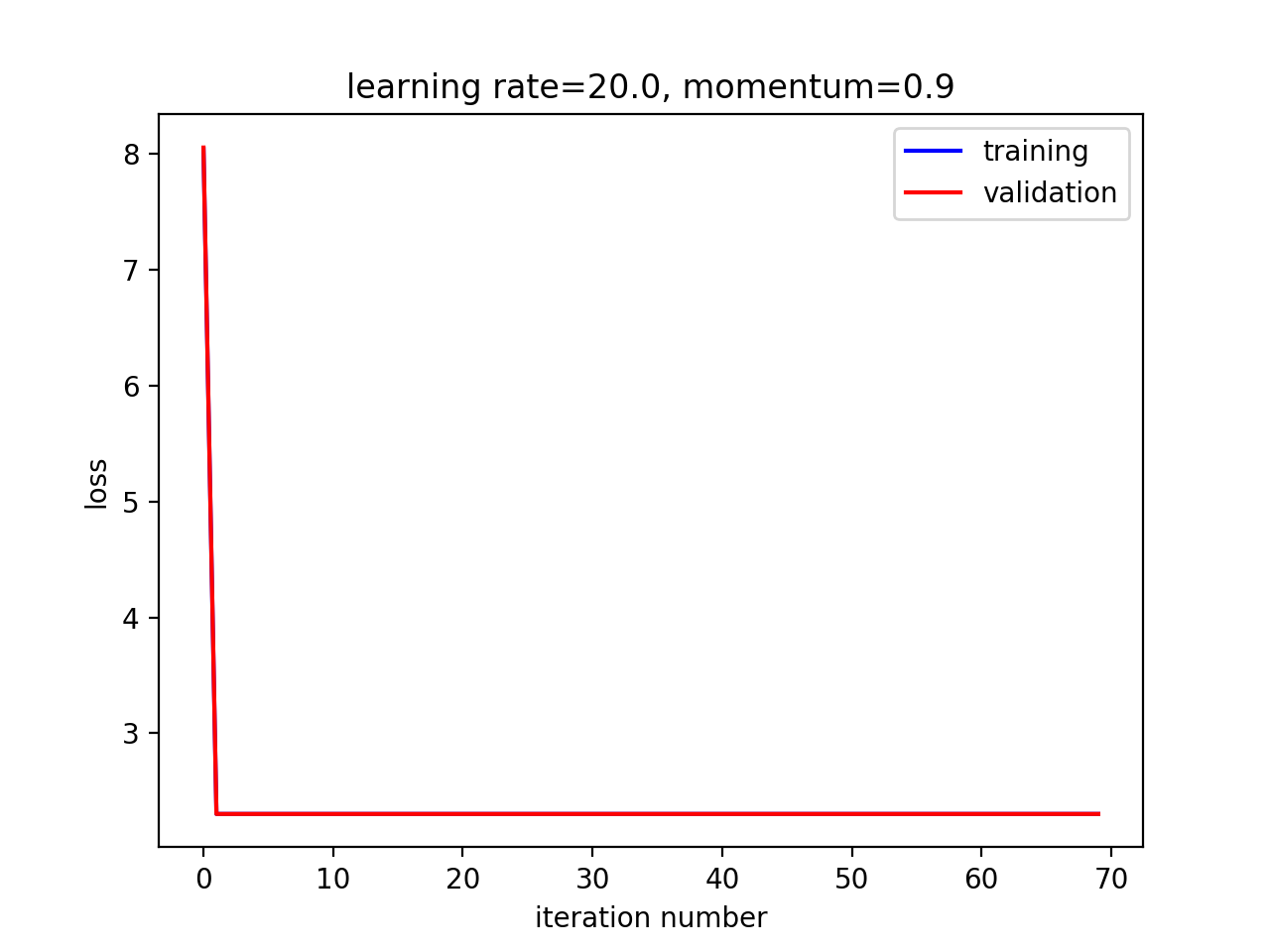
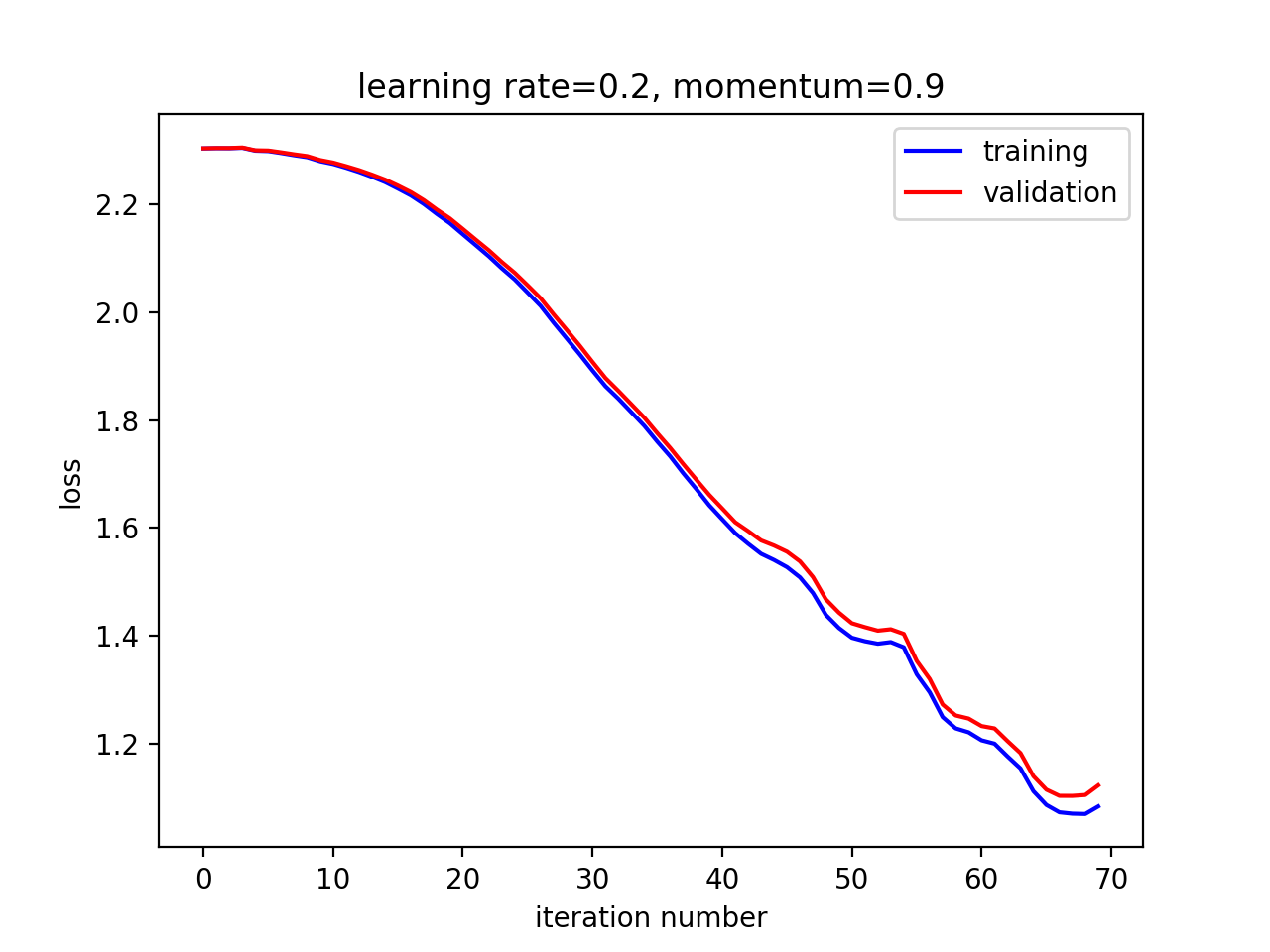
在这个例子中,小学习率,大动量取得了最佳效果。
隐藏单元数
当我们找到一组较好的超参数时,我们就可以挑战更大更复杂的模型了。模型泛化程度的指标是验证集上的分类损失,而不是正则损失。将惩罚因子设为0,隐藏单元数增加到200。
a3.a3_main(0, n_hid=200, n_iterations=1000, lr_net=0.35, train_momentum=0.9, early_stopping=False, mini_batch_size=100)
看看效果:
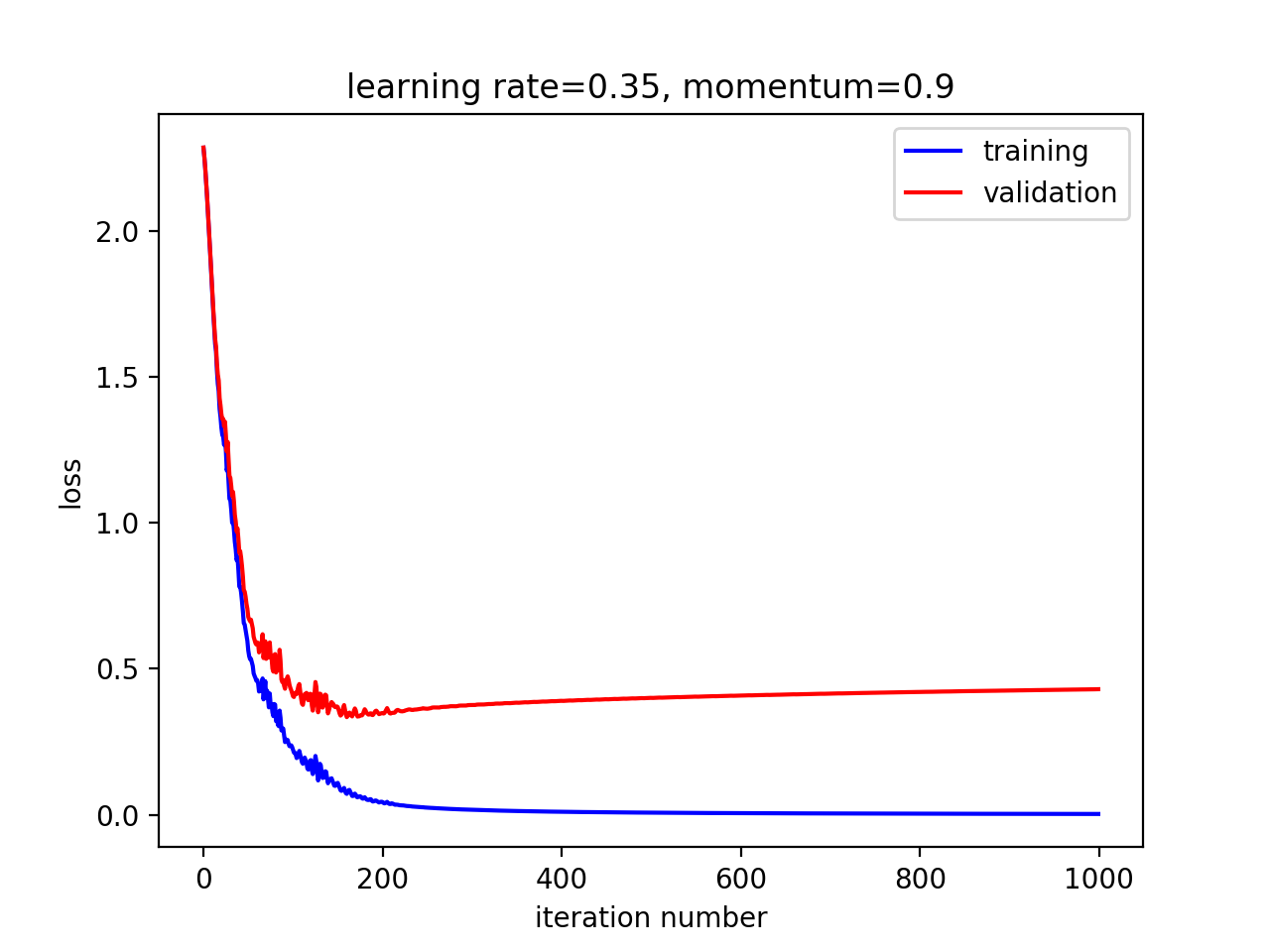
效果更好了。
early stopping
最简单的正则措施是提前终止训练,我们将在验证集上的分类损失达到最低的时候终止训练。从上图来看,大约是接近200迭代的时候,剩余的800个迭代都是在浪费时间。
打开开关:
a3.a3_main(0, n_hid=200, n_iterations=1000, lr_net=0.35, train_momentum=0.9, early_stopping=True, mini_batch_size=100)
得到:
Early stopping: validation loss was lowest after 160 iterations. We chose the model that we had then.
权值惩罚
另一个正则手段是惩罚大权值,关闭early stopping,打开权值惩罚:
for decay in [0, 0.0001, 0.001, 0.01, 1., 5]: print decay a3.a3_main(decay, n_hid=200, n_iterations=1000, lr_net=0.35, train_momentum=0.9, early_stopping=False, mini_batch_size=100) print
再来看看效果
在decay=0.0001的时候
After 900 optimization iterations, training data loss is 0.0483611028484, and validation data loss is 0.391353957494 The loss on the test data is 0.40910395955 The classification loss (i.e. without weight decay) on the test data is 0.369096931752 The classification error rate on the test data is 0.0907777777778 The loss on the training data is 0.00756094647265 The classification loss (i.e. without weight decay) on the training data is 0.00756094647265 The classification error rate on the training data is 0.0 The loss on the validation data is 0.348293958302 The classification loss (i.e. without weight decay) on the validation data is 0.348293958302 The classification error rate on the validation data is 0.085
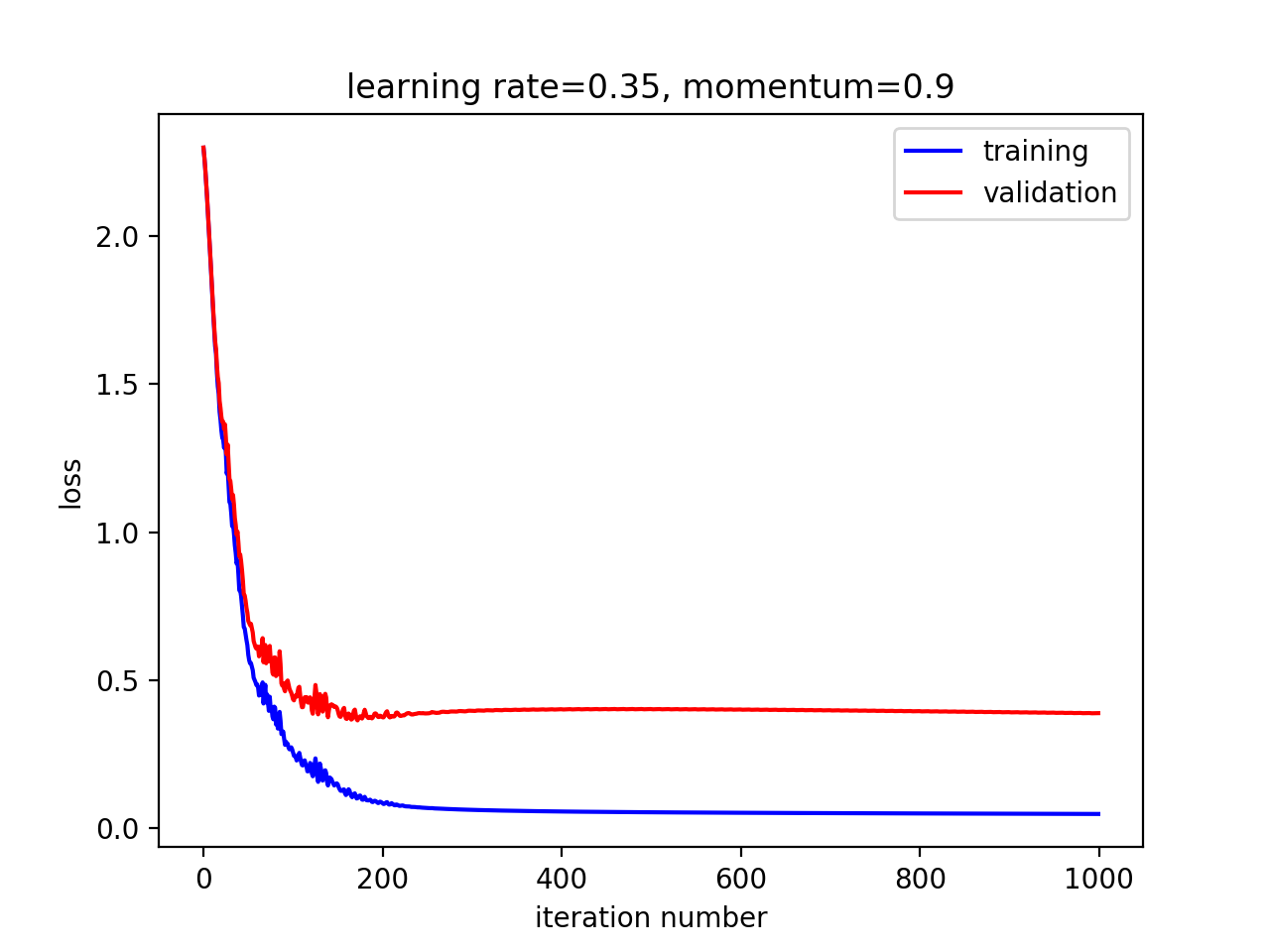
最后的手段是使用更少的参数。试验不同的隐藏节点数:
for size in [10, 30, 100, 130, 170]: print size a3.a3_main(0, n_hid=size, n_iterations=1000, lr_net=0.35, train_momentum=0.9, early_stopping=False, mini_batch_size=100) print
根据validation loss来看,最佳大约是30:
The loss on the test data is 0.364650620143 The classification error rate on the test data is 0.0872222222222 The loss on the training data is 0.00404192494518 The classification error rate on the training data is 0.0 The loss on the validation data is 0.317076694896 The classification error rate on the validation data is 0.078
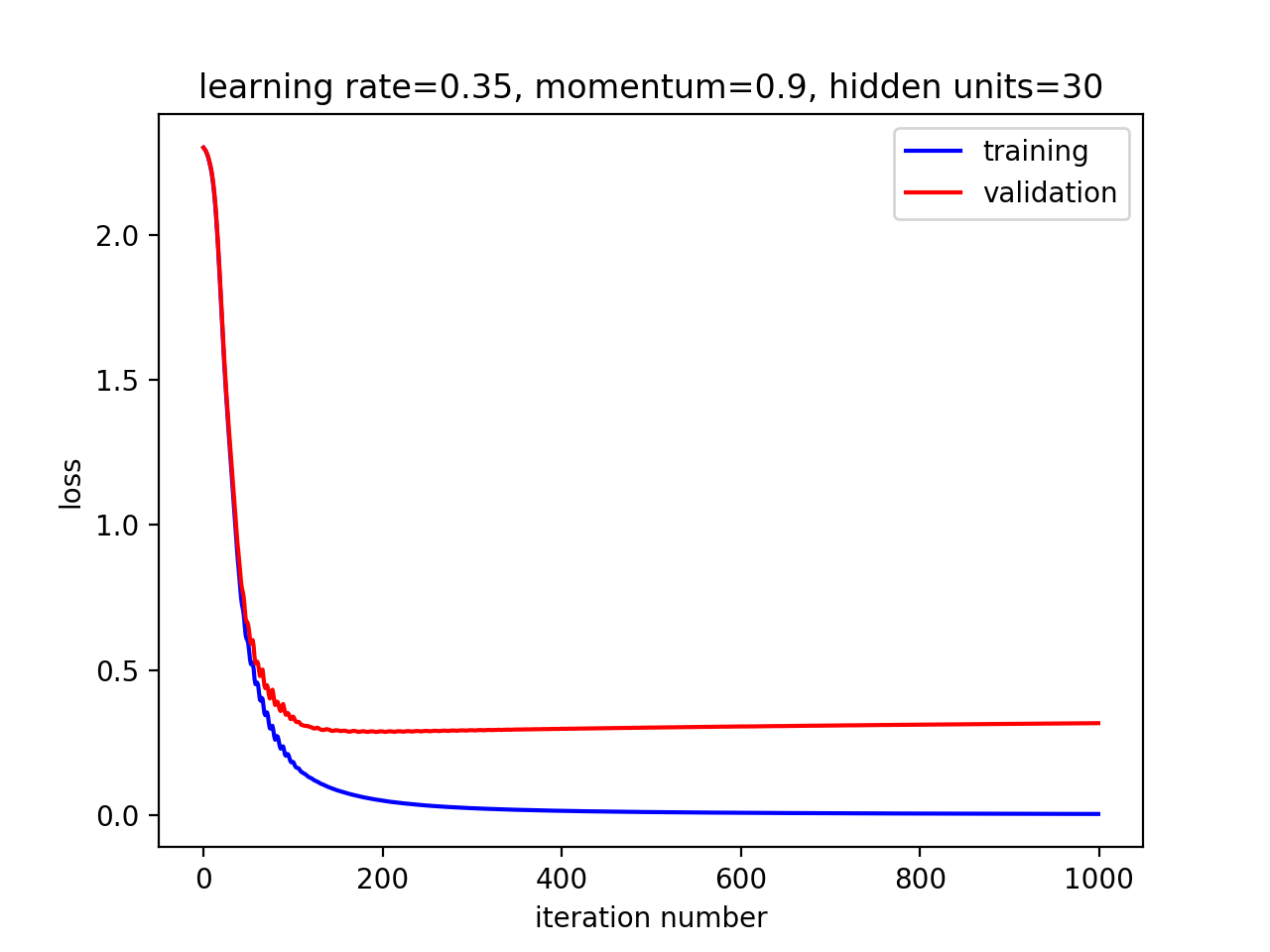
综合
当然,实践中可以结合多种手段,比如打开early_stopping:
for size in [18, 37, 83, 113, 189]: print size a3.a3_main(0, n_hid=size, n_iterations=1000, lr_net=0.35, train_momentum=0.9, early_stopping=True, mini_batch_size=100) print
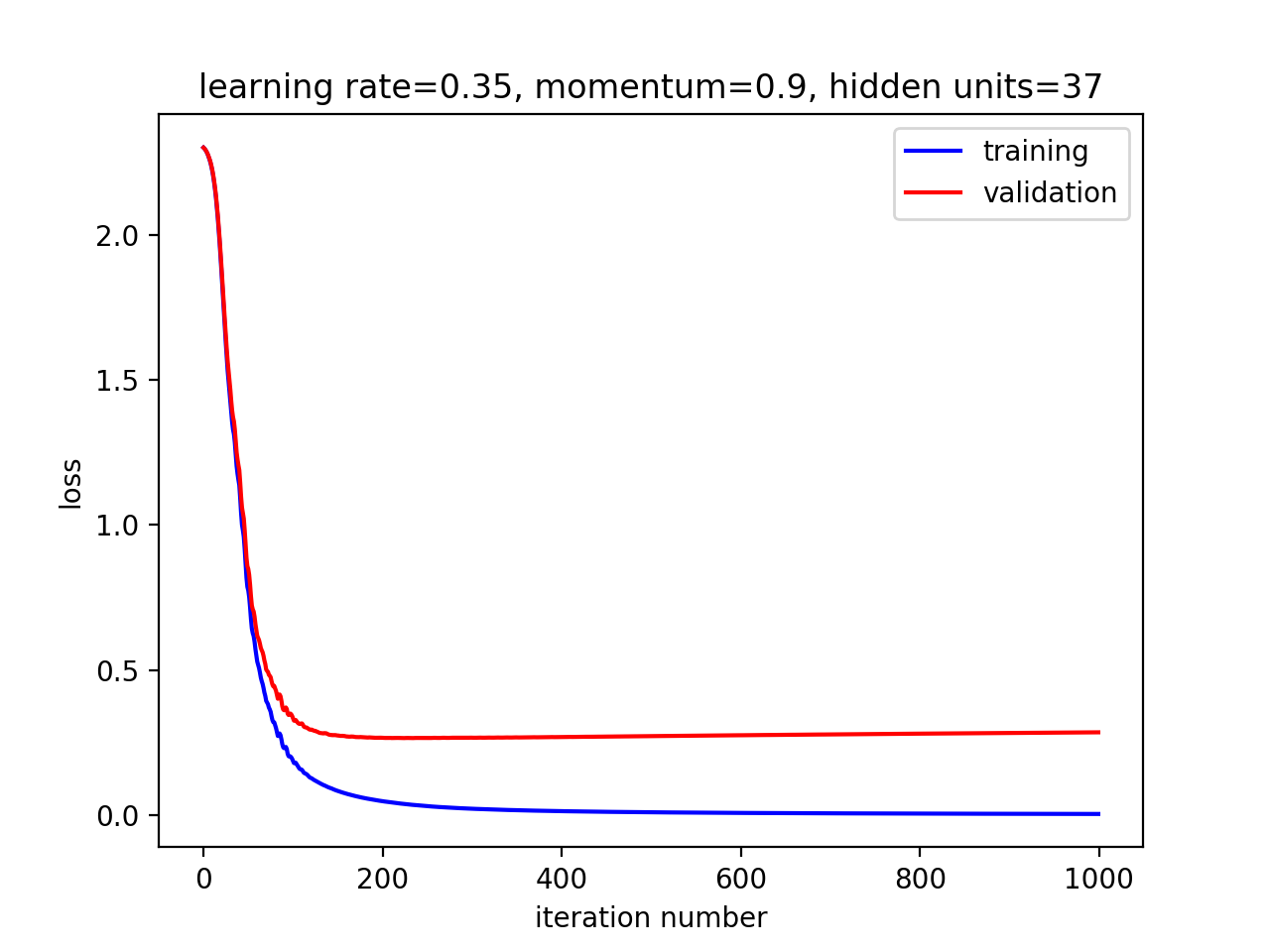
最佳hidden size大约是37:
The loss on the test data is 0.309983607422 The classification error rate on the test data is 0.0794444444444 The loss on the training data is 0.0036007342029 The classification error rate on the training data is 0.0 The loss on the validation data is 0.285084100748 The classification error rate on the validation data is 0.067
Reference
https://github.com/hankcs/coursera-neural-net
http://ufldl.stanford.edu/tutorial/supervised/SoftmaxRegression/
![]() 知识共享署名-非商业性使用-相同方式共享:码农场 » Hinton神经网络公开课编程练习3 Optimization and generalization
知识共享署名-非商业性使用-相同方式共享:码农场 » Hinton神经网络公开课编程练习3 Optimization and generalization
 码农场
码农场