码农场目录
这节课介绍防止模型过拟合的各种方法，给出了正则化项、惩罚因子的贝叶斯解读；并展示了基于贝叶斯解读的一种实践有效的惩罚因子调参方法。
复习：过拟合
训练数据中不光有正确的规律，而且还有偶然的规律（采样误差，只取决于训练实例的选择）。拟合模型的时候，无法知道规律是真实的还是偶然的。如果模型复杂度高，它有可能学到了采样误差，但泛化得很差。
防止过拟合
-
更多数据
这是最好的方法，只要你的计算力足够 -
使用复杂度恰到好处的模型
既能拟合真实的规律，又不至于学到偶然的规律 -
综合不同的模型
可以用不同形式的模型，也可以用同一种模型在不同数据子集上的训练结果（这被称为“bagging”） -
贝叶斯
使用一个神经网络结构，但综合不同的weight下的预测结果
限制神经网络的复杂度
有很多限制手段：
-
限制隐藏层和单元数量
-
以小权值起步，在过拟合前停止训练
-
L1或L2正则
-
用噪音干扰激活值
有时候会综合使用多种手段。
如何挑选控制复杂度的参数
比如隐藏单元数和惩罚因子大小等，如何确定呢？
-
错误的手段是在测试集上尝试不同的参数取最佳的一组。这听上去是个简单好用的方法，也的确有很多人在用；但实际上是错误的。不信的话换一组新的测试集试试。
-
最极端的例子是，假设测试集是完全随机的。用上述方式学到的模型却不是随机的，这时候再来一组随机的新测试数据，结果可想而知。
交叉验证：改进的调参方法
将整个数据集拆分为3个子集：
-
训练集：用来训练模型
-
验证集：用来确定最佳的训练参数
-
测试集：验证模型效果（通常比验证集上的效果要差）
具体的做法通常是N折交叉验证：先把测试集单独拎出来；然后把剩下的分为N等分，取一份作为验证集，剩下的$N-1$份作为训练集。轮换N次训练，得到关于某组超参数的N次估计。
注意这N组试验是相关的，如果所有无规律的噪音实例都落入了同一个子集，那么无论该子集是训练集还是验证集，效果都很差。
通过提前终止训练来防止过拟合
通常在计算力小而数据量大的情况下采用，这种方法不尝试多种超参数，而是开始时采用一个小权值，然后在验证集上的效果变坏的时候直接终止训练。
具体操作的时候可能较难确定确切拐点，因为误差经常上下波动。通常会超出最佳时间节点，然后折返回去。
这种方法天然地限制了模型的复杂度，因为权值很小并且来不及变大就终止了。
为什么权值小复杂度低
当权值很小的时候，对逻辑斯谛单元来讲，恰好处于其线性的部分（S形的尾部近似线性）。所以整个网络相当于线性的。
线性系统直接将输入乘上某个系数映射到输出，没什么复杂度。
限制权值的大小
L2正则通过向算是函数添加一个额外项来惩罚过大的权值，除非误差相对较大，否则保持较小权值。
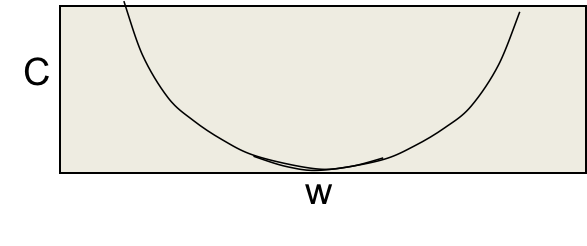
权值及L2损失函数如上图所示，是一个抛物线。其形式化的定义如下：
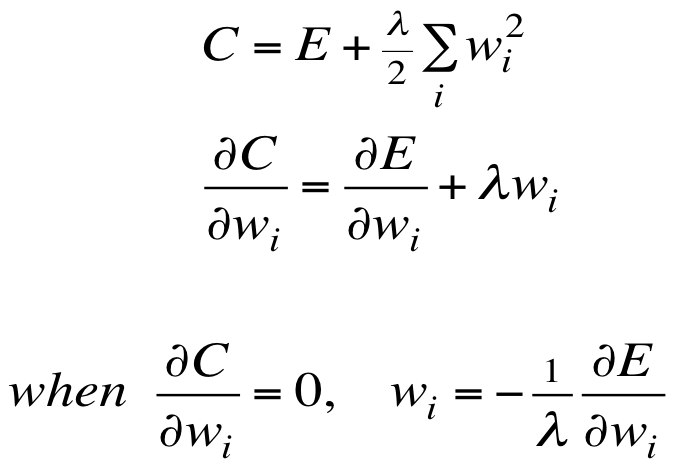
所以在损失函数的局部最小值点处（导数为0），唯一允许出现大权值的情况是，误差导数也很大。
L2权值惩罚项的作用
将L2正则项视为损失函数的一部分，这么做的目的是防止网络使用不必要的权值。通过阻止模型利用多余的权值拟合采样误差，可以使模型泛化得更好。权值较小，则输出变化得比输入慢，模型更加“平稳”。
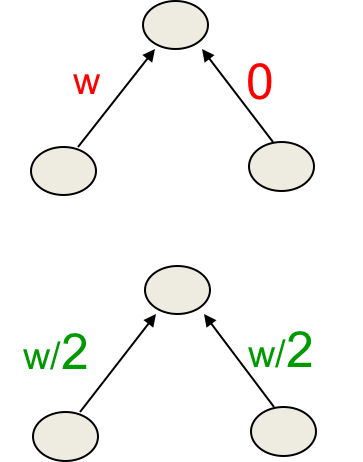
存在L2的话，如果网络有两个大小类似的输入，它会优先让两个权值平摊，而不是全推给单个权值（算算它们的L2惩罚项大小就知道了）。
其他权值惩罚方式
有时候用L1正则更好，其损失函数是V字形：
L1正则强制权值的绝对值尽量小，这很容易理解。
有时候使用更极端的惩罚方式更好，一些较大的权值反而导数更小。导数小误差变化就小，在“提前终止训练”的技巧下，会允许网络保留部分较大的权值，而不至于将权值限定在0左右。
权值惩罚与权值约束
相对于惩罚每个权值的平方和，另一种手段是限制权值平方和的最大值。如果某次更新破坏了这个限制，那就将权值向量缩放到满足约束。
后者有很多优势，比如选择超参数更方便（因为逻辑斯谛单元的0和1通常有很自然的解释）、防止权值卡在原点附近动弹不得。当一个单元触发约束的时候，惩罚效果由最大的梯度（更新量）决定。只要惩罚这个出头之鸟就行了，胜过将所有不相关的权值推向0。
使用噪音作为正则项
通过噪音实现L2正则
在使用平方误差的线性网络中，每传播一层，噪音（高斯）的方差被权值放大一次。如果输出单元是线性的话，放大的噪声会直接加到输出上去。
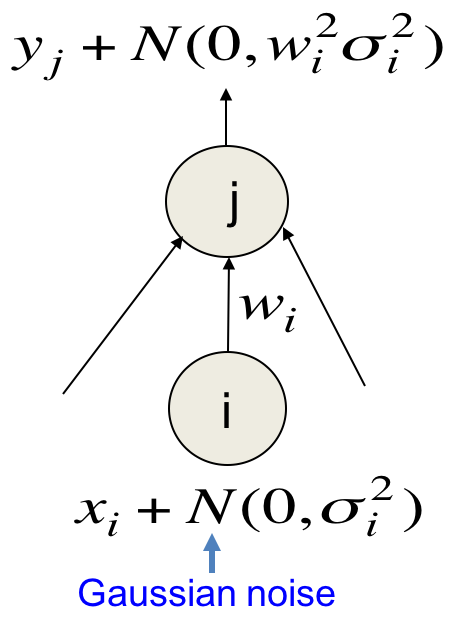
最小化这个损失函数相当于最小化与噪声无关的平方误差，以及最小化$w^2\sigma^2$。后者就相当于一个L2正则化项，推导过程如下：
这里反复利用到了$\epsilon_i$与$\epsilon_j$以及$y-t$无关的性质。
复杂网络上的噪音
在复杂网络上的噪音则不严格等于L2正则项，但比L2正则效果更好，特别是RNN中。
在激活值上引入噪音作为正则项
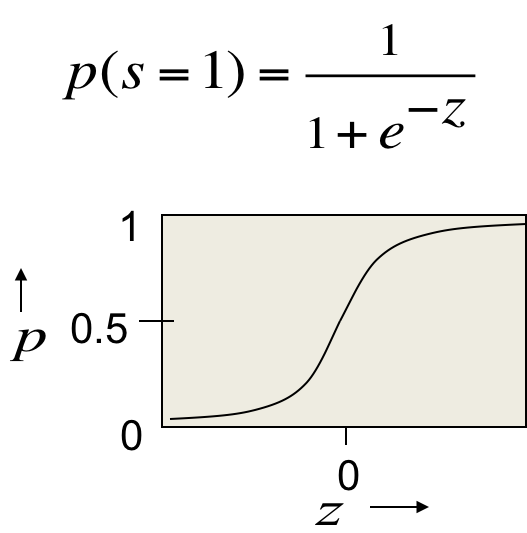
在一个逻辑斯谛单元构成的神经网络上，如果前向传播时我们让每个逻辑斯谛按照自己的激活值作为概率分布随机地输出0或1，反向传播时则使用真实值。结果是在训练集上效果变差，训练速度变慢；但在测试集上效果要好很多。
知识共享署名-非商业性使用-相同方式共享：码农场 » Hinton神经网络公开课9 Ways to make neural networks generalize better