Hinton神经网络公开课9 Ways to make neural networks generalize better

贝叶斯方法

与其找出最可能的一组超参数，贝叶斯方法考虑所有可能的超参数组合及生成给定数据集的概率。

贝叶斯框架

贝叶斯框架假设对万事万物都存在先验分布，该分布可能并不准确。给定观测数据，我们将先验分布和似然项综合起来得到后验分布。该似然项表示给定模型参数，生成这些观测数据的概率。贝叶斯方法偏好那些更可能生成给定数据集的参数。即便先验分布不准确，只要有足够的数据，似然项依然足够准确，可以接近真实分布。

抛硬币例子

假设你只知道抛硬币的结果是随机独立事件，正面是$p$，反面是$1-p$。于是我们的模型只有一个参数$p$。

当我们投掷100次，有53次正面的时候，频率学派会根据最大似然估计$p=0.53$，为什么呢？

抛硬币的数学

模型生成观测数据的概率如下：

求导，导数取0，发现$p=0.53$，这就是最大似然的数学原理。

一些问题

如果只抛一次并获得一次正面怎么办呢？

直接说$p=1$太武断了，只能说有可能是1，但从生活经验来看更可能是0.5左右。于是不如给出所有的$p$及其概率。

参数的概率分布

根据贝叶斯方法，第一个先验是假设所有的$p$都是等可能存在的。比如有些硬币永远出正面，有些硬币以0.5的概率随机出正面等等，这些硬币出现的概率都是相等的。此时p的概率密度如下：

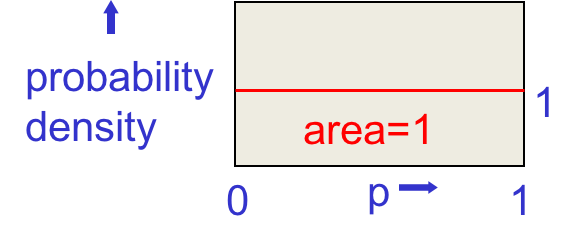
假设观测到一次正面。

红线是我们的先验，将其上的每个点都乘以根据该概率观测到正面的概率（横坐标乘以纵坐标），就会得到下图的概率密度：

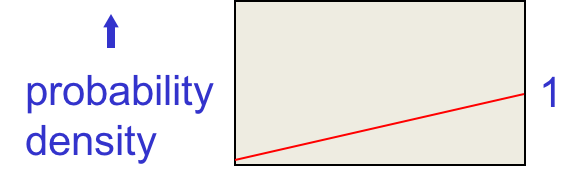
 这是未归一化的概率，缩放纵坐标归一化面积后得到：

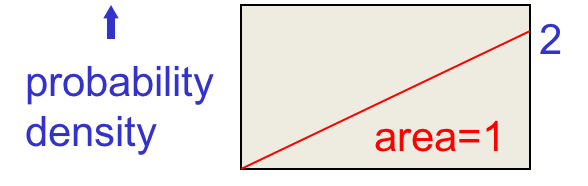
假设观测到一次背面

对每个$p$来讲，观测到背面的概率都是$1-p$，对应下图的绿线：

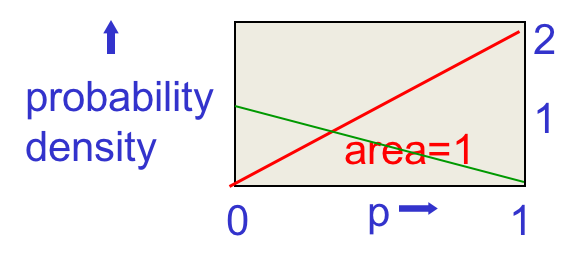
将先验概率与似然项相乘，得到如下曲线：

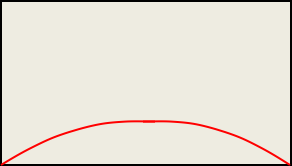
再次归一化得到：

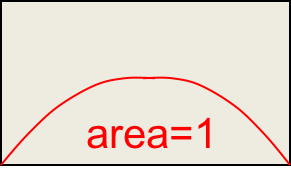
这就是观测到一次正面和一次反面的后验概率分布。从这个概率分布来看，我们直观上可以推断$p$不太可能是0或1，而有可能在两者中间。

重复98次

一共得到53次正面和47次反面之后，得到如下的曲线：

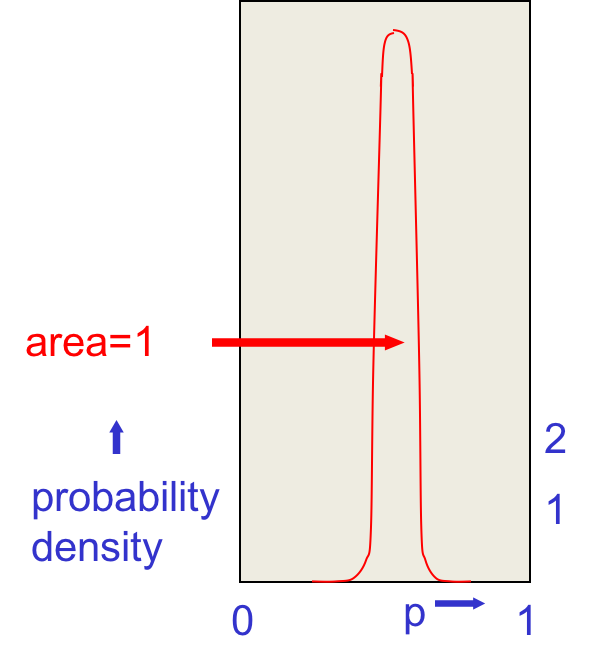
$p=0.53$时概率最大，小一点概率也很大，小太多就不大了。

贝叶斯定理

定义W为一组参数，D为一组数据，则：

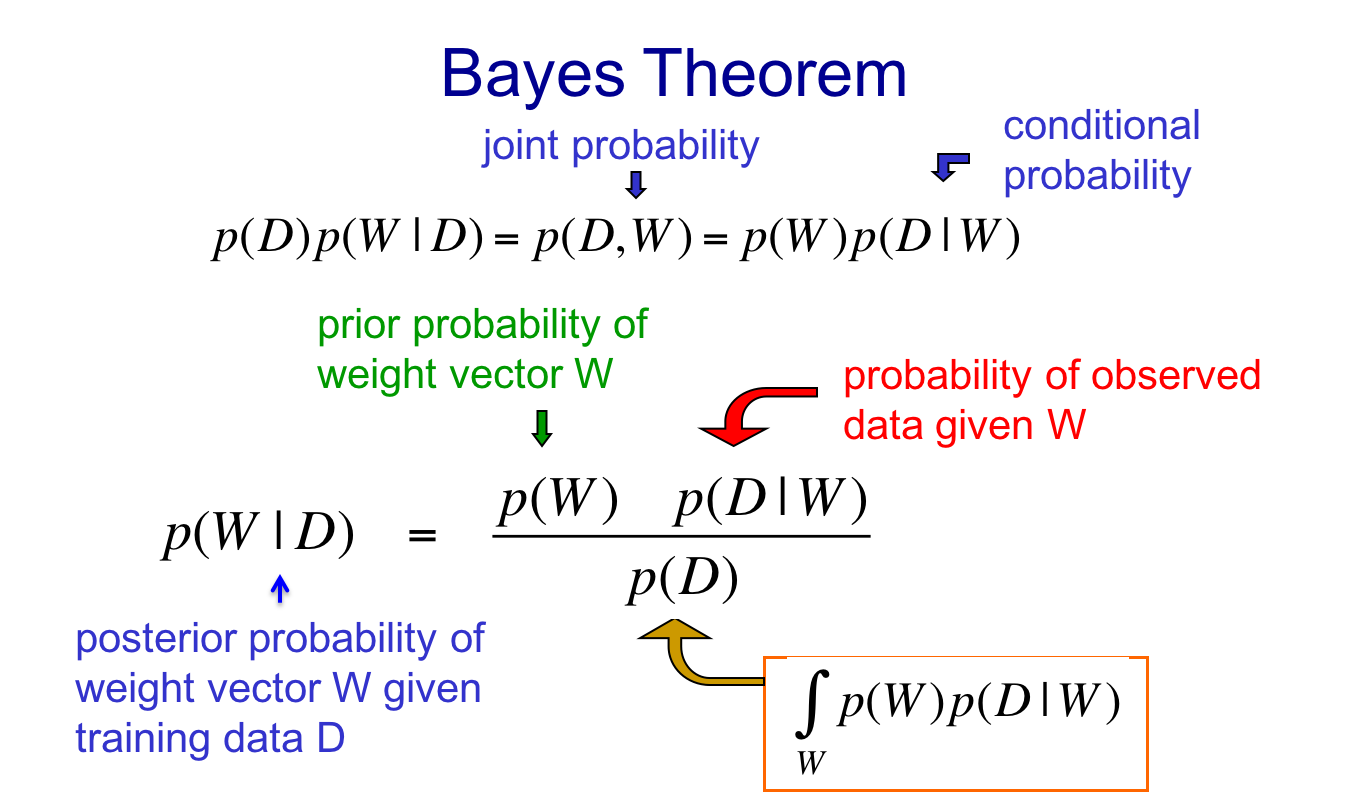
给定数据集D，某个参数向量W的条件概率等于，参数向量W的先验概率乘以，给定参数向量W观测到数据集D概率，然后通过数据集的概率进行归一化的结果。由于分母与某个特定的W无关，所以在寻找最大后验概率的时候，可以忽略这个分母。

关于权值惩罚的贝叶斯解读

在使用权值惩罚手段训练模型的时候，我们实际上在试图找出一组同时满足我们关于权值的先验知识与数据集后验概率分布的参数。

这被称作Maximum alpha Posteriori learning，给了我们一个容易理解的解释。

最大似然监督学习

寻找最小化平方误差的模型参数相当于最大化正确答案的对数概率密度。假设正确答案由均值为模型输出的高斯噪声分布生成。

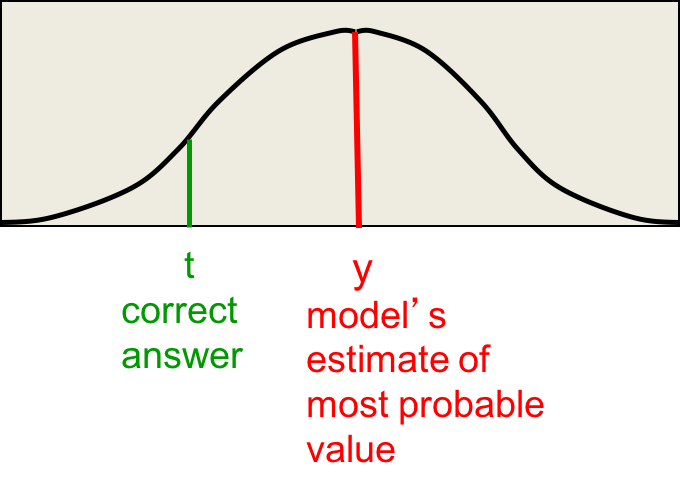
假设模型的输出为：

放到高斯分布里面去，目标值（正确答案）的概率密度为：

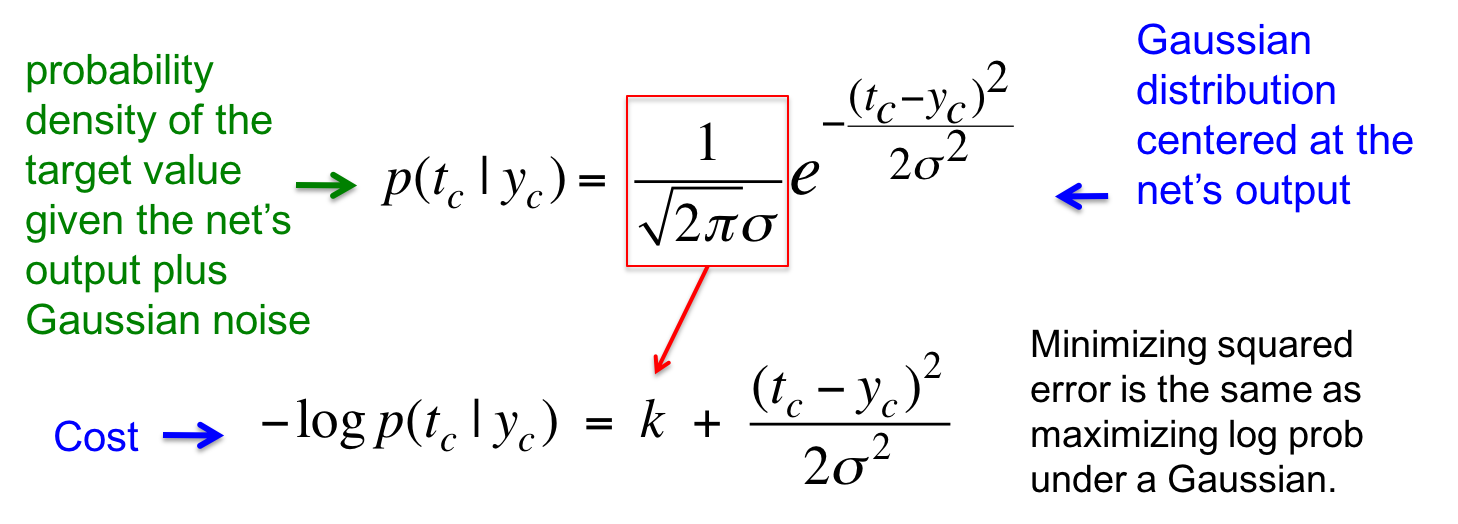
取了负对数之后，恰好得到类似平方损失函数的形式，只不过多了个常数项，以及作为分母的高斯分布的方差。所以只要见到最小化平方误差的损失函数，都可以将其解读为最大化目标值在高斯分布下的概率对数。

MAP: Maximum a Posteriori

贝叶斯方法就是找出所有权值向量满足的完整的后验概率分布。对于非线性网络来讲，如果权值很多则比较难找到，但贝叶斯学派有许多聪明的技巧去估计这个复杂的分布，比如著名的Monte Carlo方法。

当我们还是先从简单的出发吧，假设我们依然仅仅想找到一个最可能的参数向量。

• 我们可以取一个随机的初始值，然后朝着增大$p(W|D)$的方向调整它

• 但这只能达到局部最优

• 切换到对数域比概率域更方便

• 我们的根本目标是最大化在所有训练实例上生成目标值的概率之积。

• 假设在不同的训练实例上的误差彼此独立，则

• 

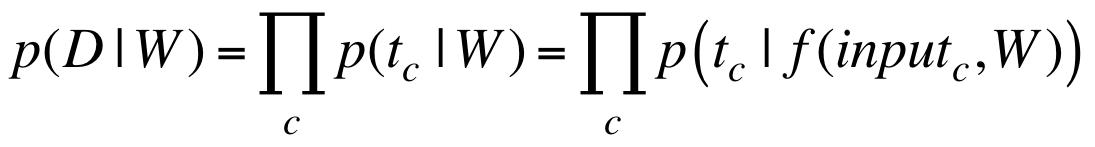
• 根据对数函数的单调性，以及考虑到计算机浮点数运算的特性，一般对两端取对数：

• 

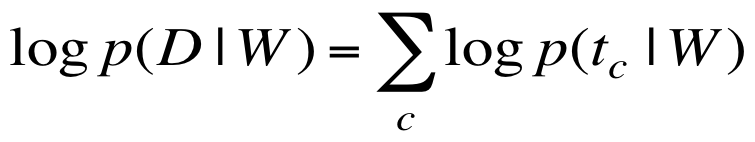
在MAP中，我们实际上寻找先验和数据的均衡：

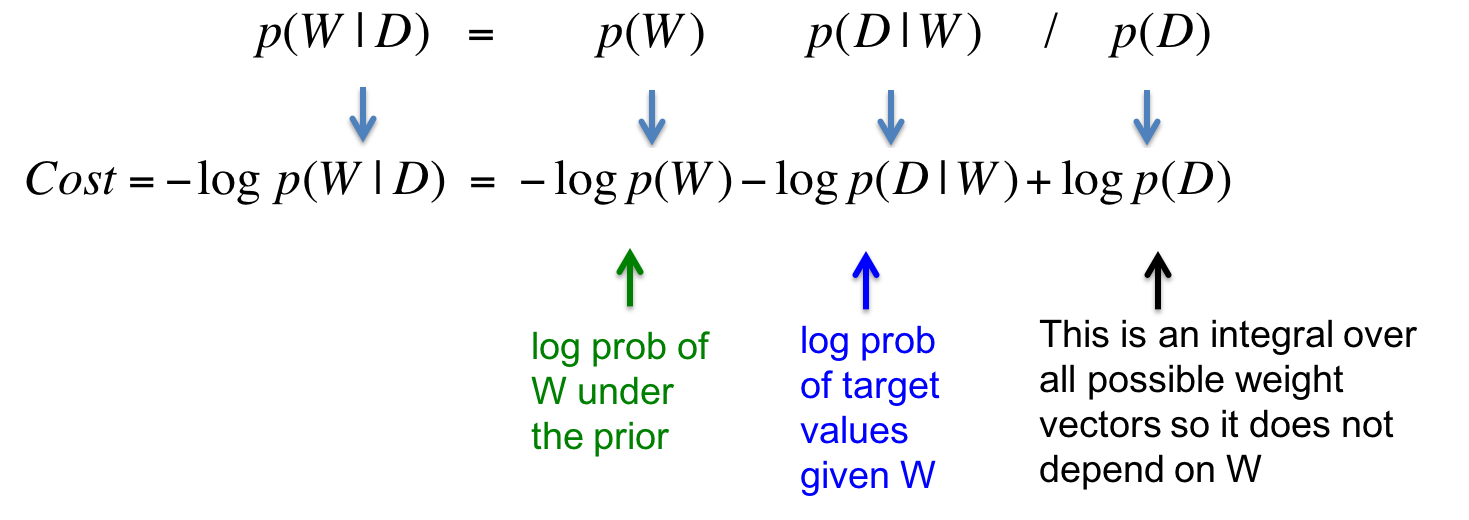
最后一项是所有权值向量下数据的概率之和，与W无关，所以可以忽略掉。中间一项就是误差项。第一项我们对W的先验。

W的先验概率分布下的概率对数

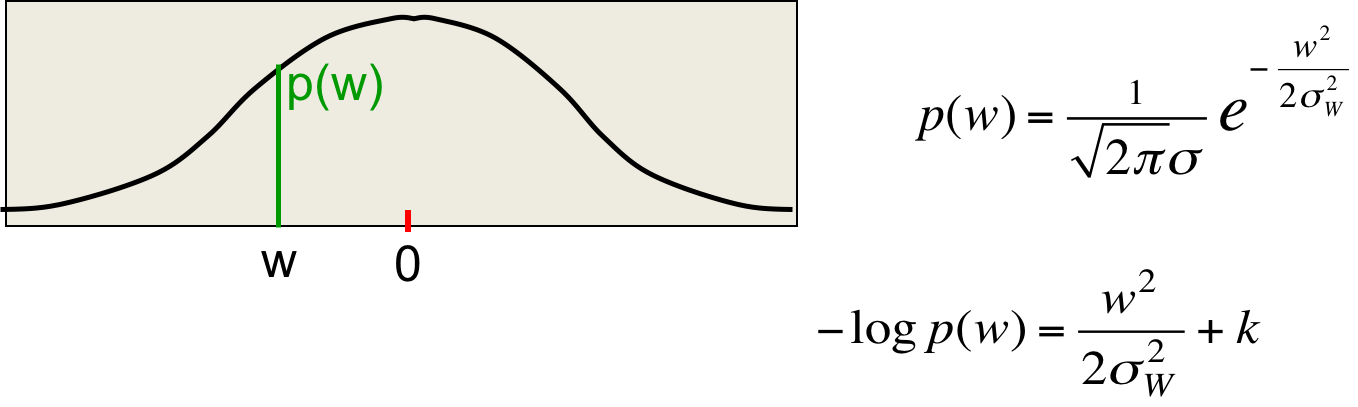
第一项的高斯解读如下，最小化参数向量的平方其实就是最大化参数向量在0均值高斯分布下的概率对数。

如果我们想要w的概率大一点，那很显然它应该接近0。

参数惩罚的贝叶斯解读

把上述知识点合在一起，就得到了最终的贝叶斯解读：

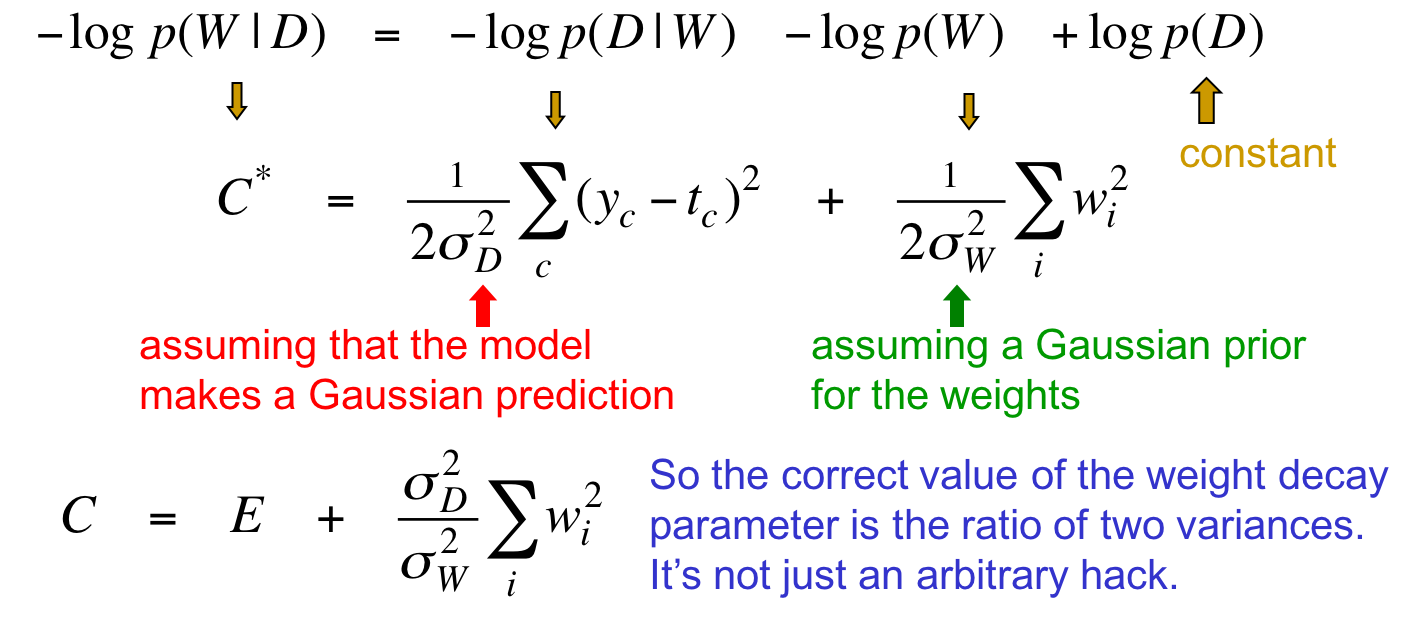
这里一共做了两次高斯假设：假设模型的预测是高斯分布，假设参数向量的先验分布是高斯分布。

在等式两边同时乘以$2{\sigma}_D^2$，得到新的损失函数$C$。其中第一项$E$恰好变成常见的平方误差。而第二项则变成了参数的平方和乘以两个高斯分布的方差的比值。该比值就是通常所说的惩罚因子。

以前一直将惩罚因子看做一个利用交叉验证集反复尝试得出的超参数，但理解了高斯解释之后，惩罚因子其实不是一个人工设定的武断的超参数，而是整个框架中两个分布的方差的比值。

确定神经网络中的惩罚因子

这一节介绍David MacKay发明的调参方法，该方法就是基于上述贝叶斯解读的。

估计输出噪声的方差

以最小化平方误差为目标训练完模型之后，我们可以找出输出噪声的“最佳值”。

• 最佳值是加入高斯噪声后最大化正确答案的概率的那个值

• 最佳值其实就是残差（误差）的方差

估计参数高斯先验的方差

先以一个初始值作为参数高斯先验的方差去训练模型，然后使用一种叫“empirical Bayes”的dirty trick。

• 将先验的方差设为模型已学到的参数的方差。这是个“大逆不道”的做法，我们在用数据本身去决定自己的先验！

• 具体做法是用零均值的高斯分布去拟合已学到的参数值，然后用拟合到的高斯分布的方差作为先验分布的方差。这种做法有个副产品，就是可以为不同参数子集（比如不同的层）学习不同的方差

• 整个过程不需要验证集，可以用整个训练集

MacKay法

将这些知识综合起来，就得到了MacKay的方法：

• 以某些对噪声和先验的方差的初始值的比值作为惩罚因子，训练模型

• 然后将噪声方差设为误差的方差，参数先验的方差设为参数的方差，两者比值作为新的惩罚因子，训练模型

• 反复重复上一个步骤

虽然理论上无法解释，但实践效果很好

 知识共享署名-非商业性使用-相同方式共享：码农场 » Hinton神经网络公开课9 Ways to make neural networks generalize better