Hinton神经网络公开课8 More recurrent neural networks

首先简要介绍Hessian-Free优化理论。这是块硬骨头，并不要求一定掌握。

在给定方向上的移动能够将误差降低多少

在训练神经网络的时候，我们想要在error surface上尽量多地下降。梯度有了之后，具体能够迈多大一步呢？以二次曲线为例，给定曲线，假设其曲率为常数，并且假设梯度随error下降而减小。误差的最大减小量取决于梯度与曲率的比值，不同的方向梯度与曲率都可能不一样。

比如：

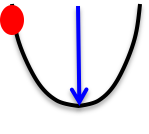
横轴是weight，纵轴是error（可以想象这是碗状凸函数的一个纵切面）。从红点出发能够获得的最大error减小量为蓝色箭头。

如果以另一个方向做切面，则可能得到如下曲线：

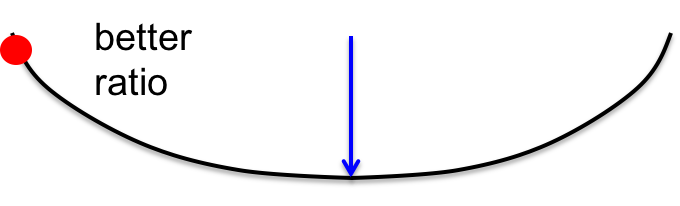
虽然梯度更小，但曲率小的更多，两者比值反而更大，error下降量就更大了。

那要怎样才能找到第二种方向呢？

牛顿法

二次error surface上梯度下降法的问题是，梯度指向最陡峭的方向，但不一定是error下降最快的方向。只有error surface的横截面是圆形的时候，梯度才是下降最快的方向。所以牛顿法的思路是利用线性变换将椭圆转化为圆。

具体做法是将梯度向量乘以曲率矩阵（海森矩阵）的逆：

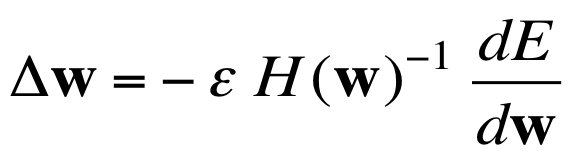
思路是极好的，在二次曲面上选好$\epsilon$可以一步到位直达最小值。但对于百万维度的weight来讲，曲率矩阵有一万亿个元素，计算不可行。

曲率矩阵

曲率矩阵的意义如下：

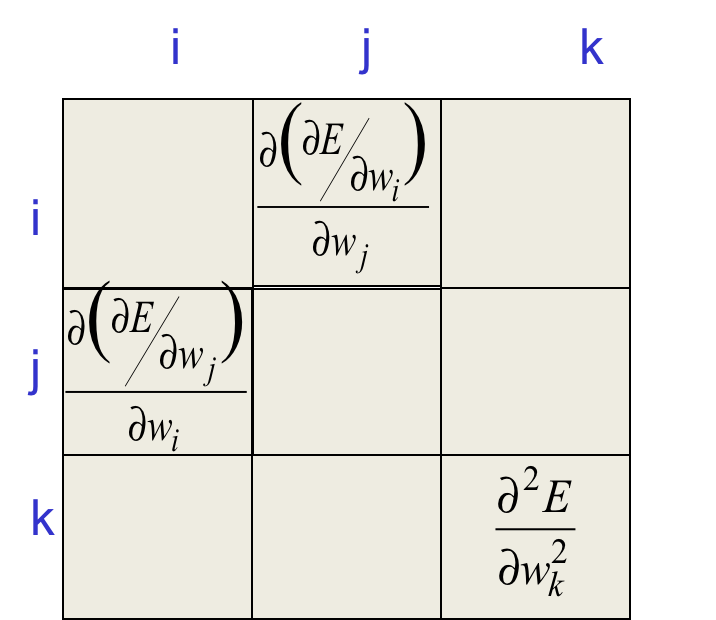
非对角线每个元素代表改变某个维度的权值，会引起误差关于另一个维度的权值的梯度如何改变。而对角线上的元素则表示改变某个权值，误差关于该权值的梯度如何变化。两者是统一的。

非对角线上的元素其实表示error surface中梯度的“纠缠（twist）”，如果沿着某个方向移动，则梯度在另一个方向的梯度会发生改变。如果error surface横截面是标准的圆形的话，所有非对角线的元素都将是0。

steepest梯度下降的问题是，在椭圆形的error surface上往一个方向（维度）移动的时候，另一个方向上的梯度会发生改变。如果改变其他维度上的权值，则当前维度上的梯度会受到影响，它们是纠缠在一起的。如果同时更新所有权值的话，可能会适得其反。其他维度上的变化可能会使当前维度上的梯度改变符号。

总之，曲率矩阵决定这种“纠缠”的具体大小，

如何避免对大矩阵求逆

Le Cun提出可以只考虑主对角线元素，但主对角线只是矩阵的一小部分。

另有许多近似曲率矩阵的方法，比如Hessian-free或LBFGS。在HF中，我们求一个近似值来代替真实值，通过一种叫Conjugate gradient的技术最小化误差，然后继续求近似值……在RNN中，还需要避免剧烈改动隐状态，这可以通过惩罚因子实现。

Conjugate gradient

只简要介绍一下，这是替代求解海森矩阵的逆直达最优解的一种方法。它不是同时改变所有维度上的权值，而是一次只在一个方向上做改动。每改动一次，都会在这个方向上达到最优（可能需要一些计算）；聪明之处是，在接下来的改动中，都不会抵消已有的优化。方向的选取上，要求新的方向与前一个方向是Conjugatede的。Conjugatede的意思是，在新方向上的移动不会改变之前方向上的梯度。

图解Conjugate gradient

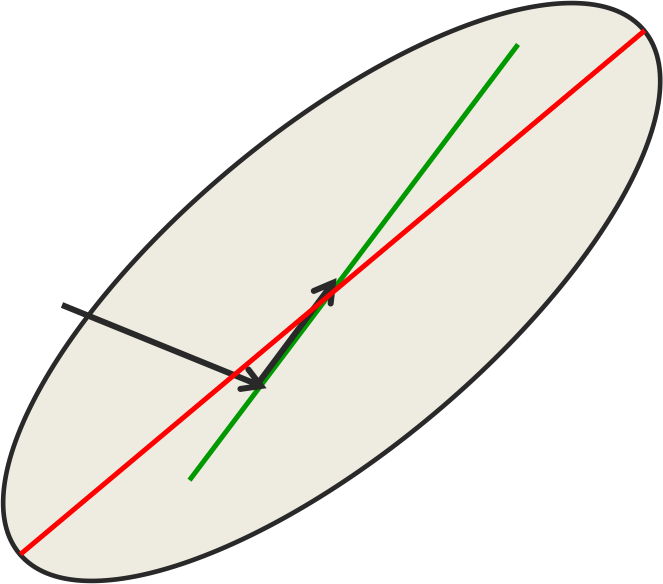
红线是山谷的底端，如果角度正确，红线上的梯度能达到0。但黑线的角度不是，我们以黑线方向接近红线，然后沿着红线走一段。由于红线是山谷谷底的方向，沿着谷底走是最佳的。但黑线方式上的极值点并不在红线上，我们可能稍微越过了一点。

接下来通过Conjugate gradient找出了一个方向，也就是绿线。绿线上所有点在第一个黑线方向上的梯度都是0，于是放心地在绿线上找一个最小值点。由于这是二维的，所以第二步就得到最优解。对于高维error surface，反复地轮换方向，由于在所有方向上都达到了最优解，所以也就到达了最优解。

Conjugate gradient的作用

在N步之后，Conjugate gradient保证能够到达N维error space的极值点。往往在远小于N步的时候，Conjugate gradient就已经非常接近极值点了。所以实践中往往不做完N步（做完N步复杂度跟求H的逆一样大）。

对非二次error surface，也可以应用Conjugate gradient（non-linear conjugate grad），效果要差一点。HF optimizer 通过将真实error surface近似为二次，来取得较高性能。

为文本序列建模

这一节应用HF到序列建模任务上去。

字符级模型的优势

自然语言处理中最常见的文本单位是词，这里为什么要用字符呢？

• 互联网是由字符组成的

• 任何足够强大的方法都会觉得学习“哪些字符构成词”是不必要的

• 词语切分预处理非常麻烦（英语时态单复数、缩写、命名实体以及类似词素又不是词素的部分。老爷子说以sn开头的词汇都跟鼻子有关。比如sneeze、snot。有人可能说snow就不是啊？可snow还被用来指代可卡因，因为是用鼻子吸的！）。在诸如芬兰语之类的黏着语中，存在一个很长很长的词语表达其他语言中几个词语的意思。

网络结构

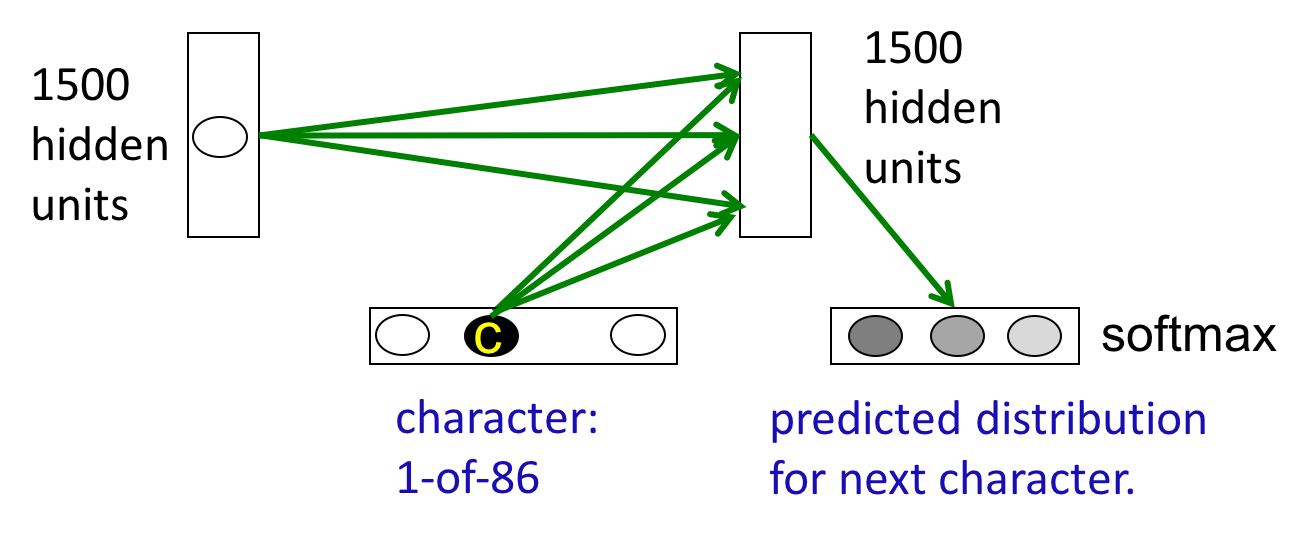
隐藏层和输入的当前字符共同影响隐藏层，输出到softmax层决定下一个字符的概率分布。预测86个字符比预测10万个词语要简单很多。

RNN中的字典树

在传统的trie中，每个节点都是FSM中一个唯一的状态。

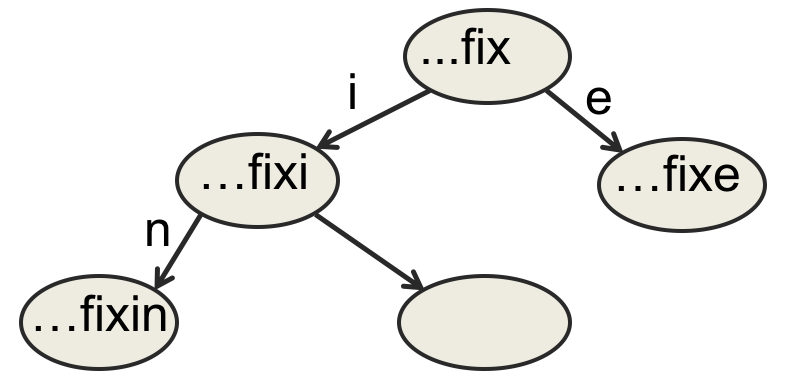
如果字母表大小是86，最长的词语长度为N，则空间复杂度是$86^N$。

而在RNN中，每个节点都是一个被所有节点共享的hidden state vector，每接受一个字符，hidden state vector被更新为一个新的vector。

• 好处除了空间复杂度之外，还可以让不同的节点共享知识。比如ing这个后缀往往接在动词后面，而不仅限于接在fix这个词后面。

• 下一个hidden state vector需要根据当前hidden state vector和当前输入字符联合决定。

Multiplicative connections

当前字符提供输入的方式也有讲究，不是将其拼接到hidden state vector上去，而是通过它选择hidden-to-hidden权值矩阵。不过这样就需要86x1500x1500个参数了，会过拟合。我们希望不同的字符选择不同hidden state vector，但相似的字符应该得到相似的hidden state vector，比如数字8和9。

使用factor进行乘法式的interaction

我们想将hidden state vector和输入混合起来，除了拼接外另有一种乘法式的混合方法，称作factor。

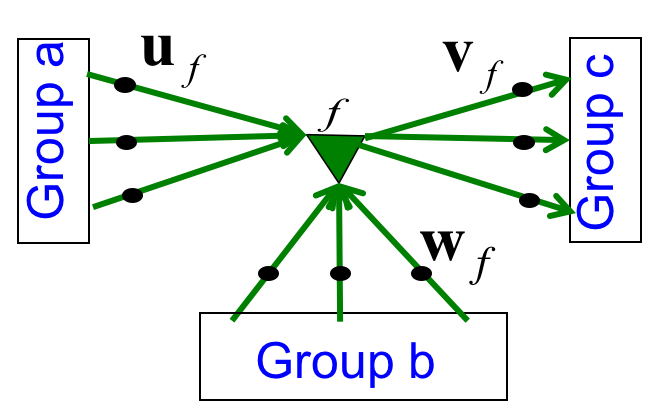
上图中间的三角形f就是factor，它首先让a和权值相乘得到一个标量，同理对b得到另一个标量，然后将两个标量相乘再乘以输出connection上的权值得到最终输出。

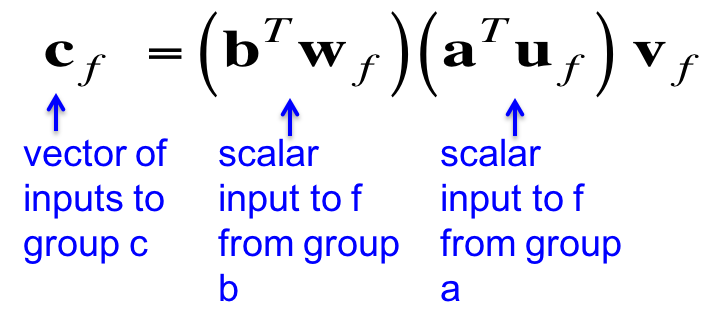
这个公式看上去的确有些奇怪，似乎两种信息混合后只得到了一个标量，反而connection上的权值缩放后倒成了最终输出。

但这只是表象，如果我们把公式变一下形，得到：

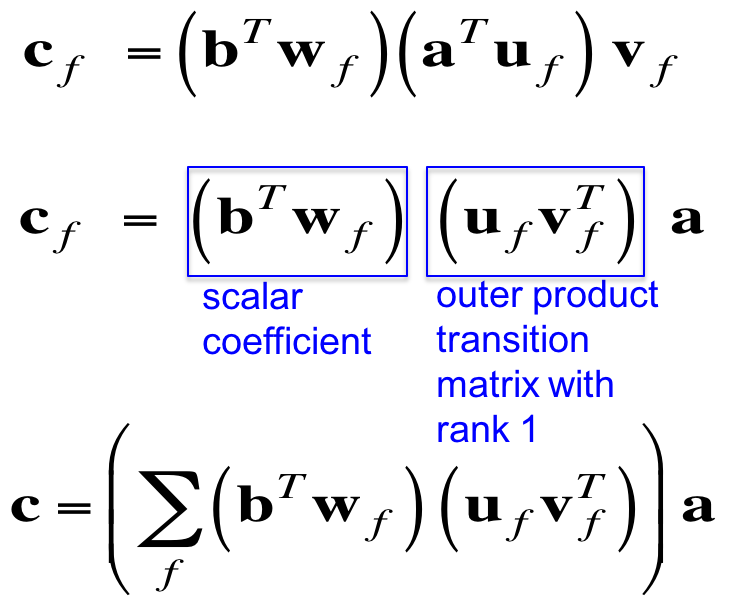
第一个蓝框是一个标量系数，第二个是秩1的变换矩阵；于是每个factor实际上定义了一个从a到c的变换矩阵（有点像卷积核）。

整体结构

对1500个hidden units（这也是FSM中node的vector的维度）的网络来讲，一共有1500个factor。因为hidden to hidden是全连接的。

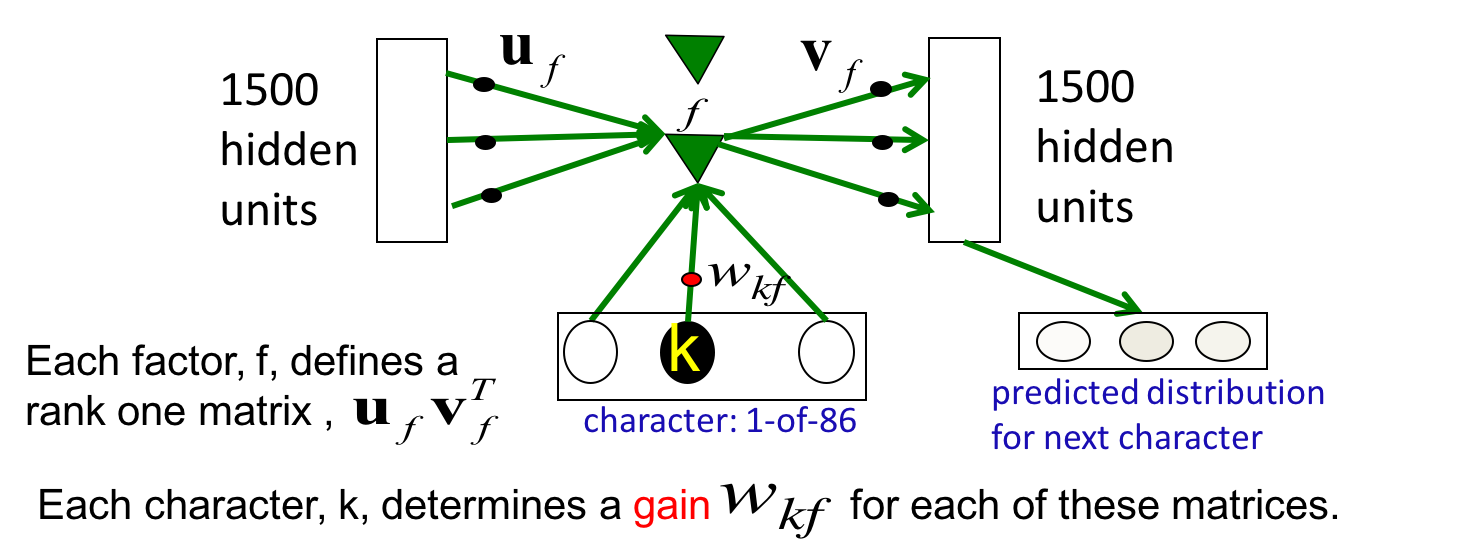
另外值得注意的是，字符是one-hot的，所以任何时刻只有一个weight标量在起作用。这个标量可以看做一种“增益”。

 知识共享署名-非商业性使用-相同方式共享：码农场 » Hinton神经网络公开课8 More recurrent neural networks