码农场目录
利用RBM为实值数据建模
这一节讲解如何用RBM去model实值数据，思想是用线性高斯单元（linear Gaussian units）代替可见层的二值随机单元。为了便于训练，还需要将隐藏单元换成rectified linear units。
为实值数据建模
对于手写数字图片来讲，其中介于黑白之间的灰色像素可以视作“mean-field” 逻辑斯谛单元（Instead of using units that have stochastic binary states, it is possible to use "mean field" units that have deterministic, real-valued states between 0 and 1, as in an analog Hopfield net.）的激活值，这是一个代表该像素被涂黑的概率。
但对真实照片来讲则不行，因为真实照片中的每个像素几乎都是周围照片的平均，在均值处有很高的概率密度，而在其他位置则很低。逻辑斯谛单元无法表达这样的概率分布。
实值可见单元的一种形式
将像素视作高斯随机变量，定义能量方程：
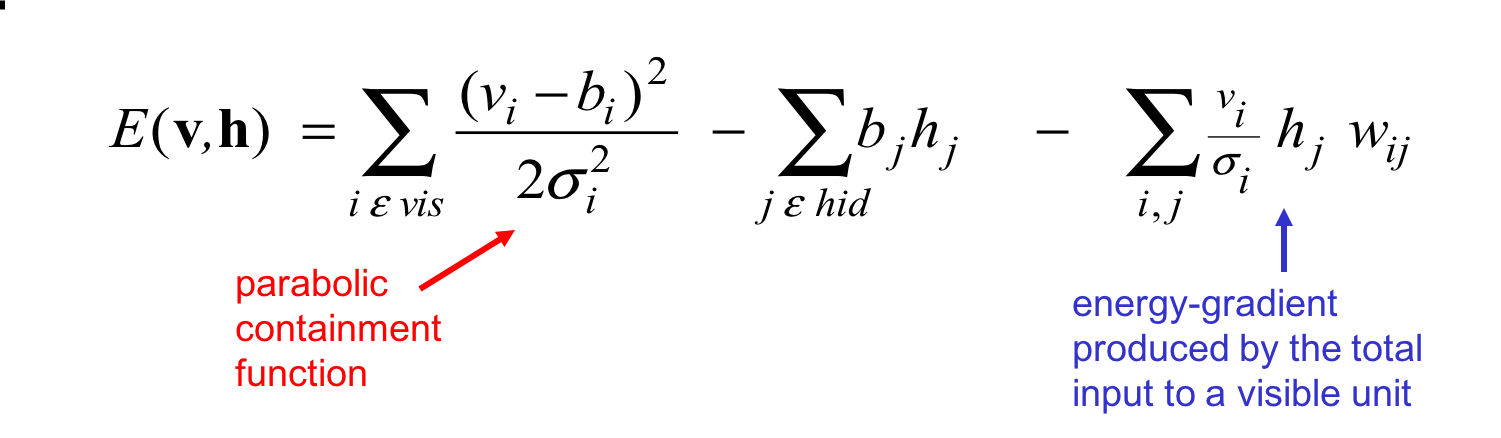
红色指向的是整个第一项，不是分母。对应下图的红色抛物线：
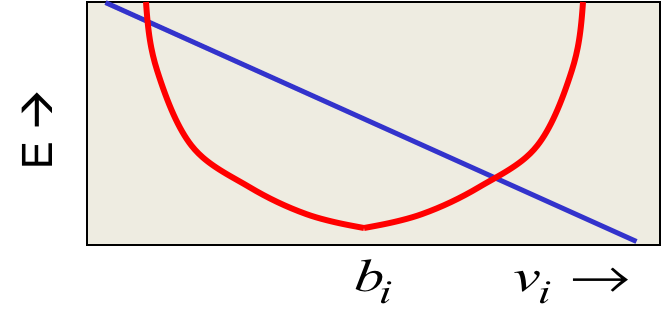
蓝色指向的项对$v_i$求导得到常数，所以是一条直线。剩下的部分是一个常数项。将三者加起来得到最终的能量方程。蓝色直线实际上是将均值$b_i$往一边拉，拉的程度取决于直线斜率。
Gaussian-Binary RBMs
上述能量方程及其导数是简单的，但训练起来是困难的，很难学习到可见单元上紧凑（应该指的是数值小）的方差。原因参考如下图解：
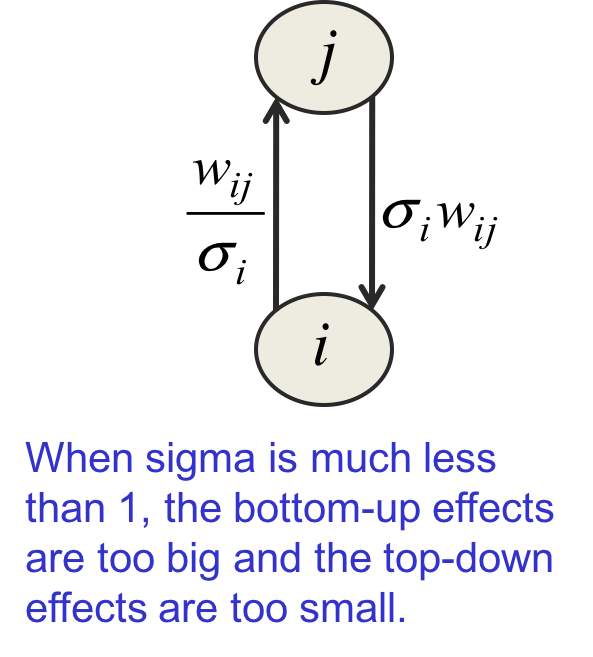
当标准差$\sigma_i$非常小的时候，从可见单元到隐藏单元的输入（弧上标的表达式）非常大，而反向的输入又非常小。算法一会儿关闭隐藏单元，一会儿又打开它，这会恶化训练效果。解决方案是增加隐藏单元数，虽然从隐藏单元到可见单元的权值依然很小，但许多个这样的弧共同贡献的效果累加起来依然会很大。
Stepped sigmoid units：一种实现实值的优雅方式
复制随机逻辑斯谛单元多份，权值相同，但偏置分别偏移为：
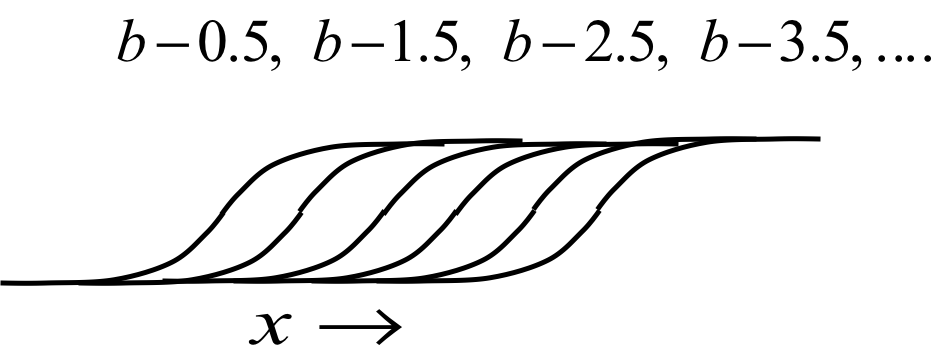
在$\sigma_i$非常小的时候，$x=\frac{w_{ij}}{\sigma_i}$会增大，于是更多的隐藏单元被激活，从隐藏单元到可见单元的累加输入值会增大，这正是我们想要的效果。
高效近似
但这么多逻辑斯谛单元的计算还是个很昂贵的问题，有种近似叫做rectified linear units，效果也很好。
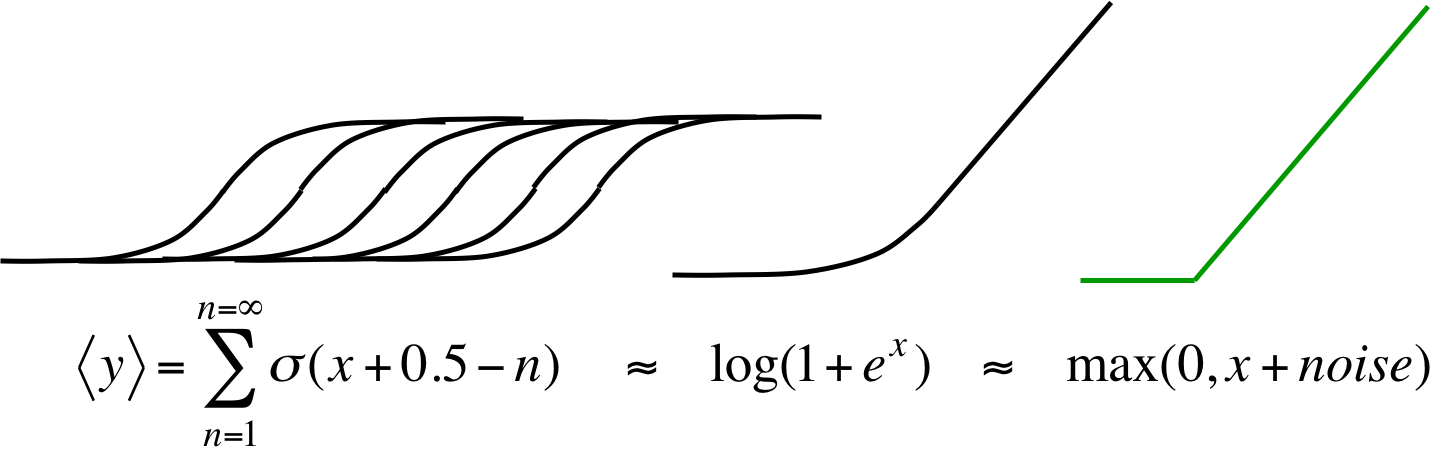
每个函数头上是自己的图像。
Contrastive divergence learning也兼容这种单元，噪音方差是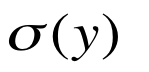
。
rectified linear units
这种单元的黑话缩写是relu，relu有种scale equivariance：
也就是说，输入x缩放a倍，激活值也缩放a倍，“but”后面的部分只是说明这不是个严格的线性单元而已。
这有点像无池化情况下CNN的translation equivariance：
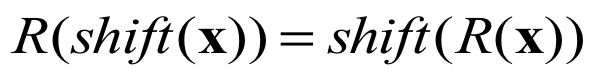
RBMs是Infinite Sigmoid Belief Nets
这一节是高级话题，本来不适合放到第一门神经网络课中。但它在数学上很漂亮，所以Hinton忍不住放进去了。
关于为什么layer-by-layer learning有效的另一种观点
RBM和使用相同权值矩阵的无限深度网络是等价的，在RBM的equilibrium distribution态时进行的马尔科夫链采样可被视作sigmoid belief net，下面是图解。
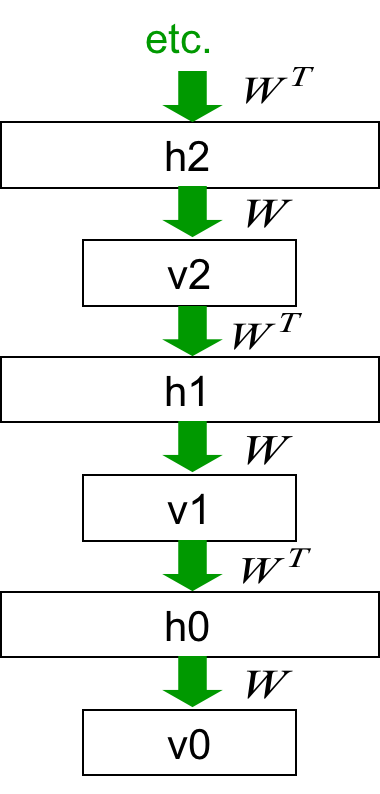
这个无限深度的有向网络生成的分布，恰好就是由W定义的一组条件分布：$p(v|h)$和$p(h|v)$对应的equilibrium distribution。
从顶而下的pass完全等效于让RBM进入equilibrium状态，也就是说这个网络定义的分布与RBM是一致的。
infinite sigmoid belief net中的推断
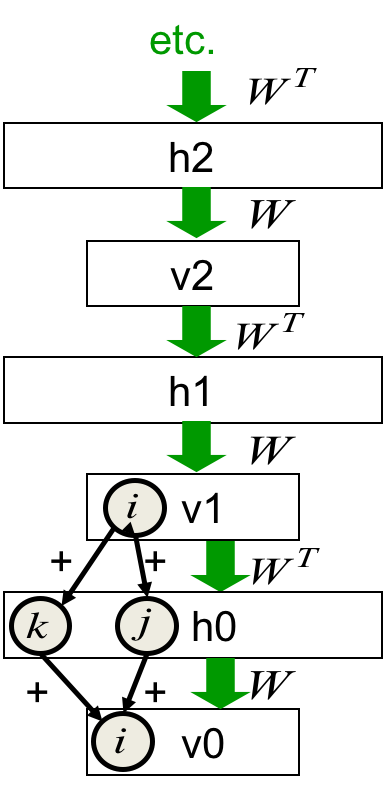
上次课程中谈到，由于explaining away的存在，很难由v0推断h0。将v0的状态向量乘以W的转置输入逻辑斯谛函数作为h0中随机二值单元的概率分布然后采样得到h0的二值向量。然而权值同样很大的k和j在这个后验概率分布的采样上会呈现出负关联的现象，哪怕它们本来是独立的。
但h0上面的所有层提供给h0的先验可以抵消explaining away，v0乘以$W^T$实际上得到的是最大似然项和先验项的乘积。在这个有向网络中进行的推断完全等效于让RBM从datavector起步到达equilibrium状态。
还可以从sigmoid belief net的训练中推导出RBM的训练。sigmoid belief net 的 learning rule 是：
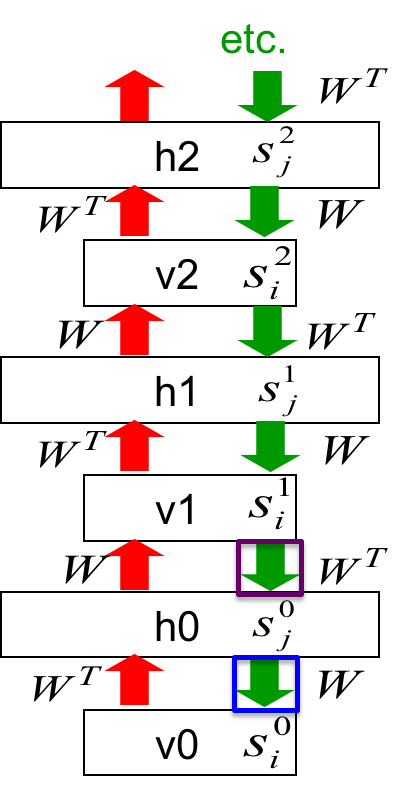
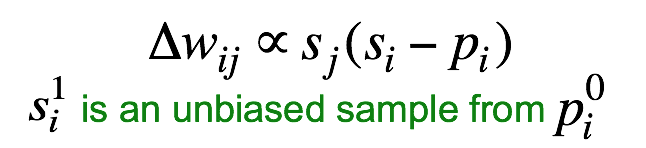
注意到这个网络中，得到$s_i^1$与得到$p_i^0$的过程是完全一致的。都是给定h0的vector，乘以W输入逻辑斯谛方程得到一个后验概率然后采样。 由于权值在所有层都是一样的，所以所有对W的更新都会累加到同一个W上去：
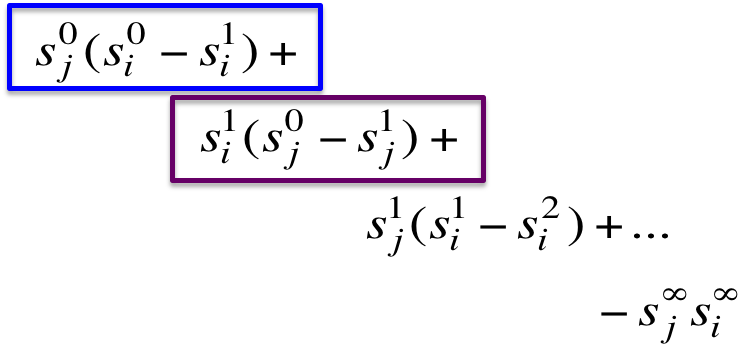
展开发现每一项首尾抵消，最终恰好得到RBM的learning rule：
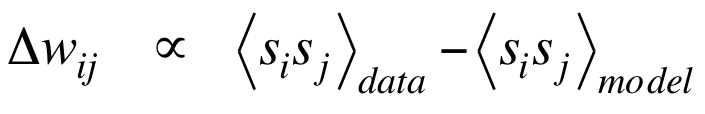
训练深度有向网络
所以这两种网络是等效的：
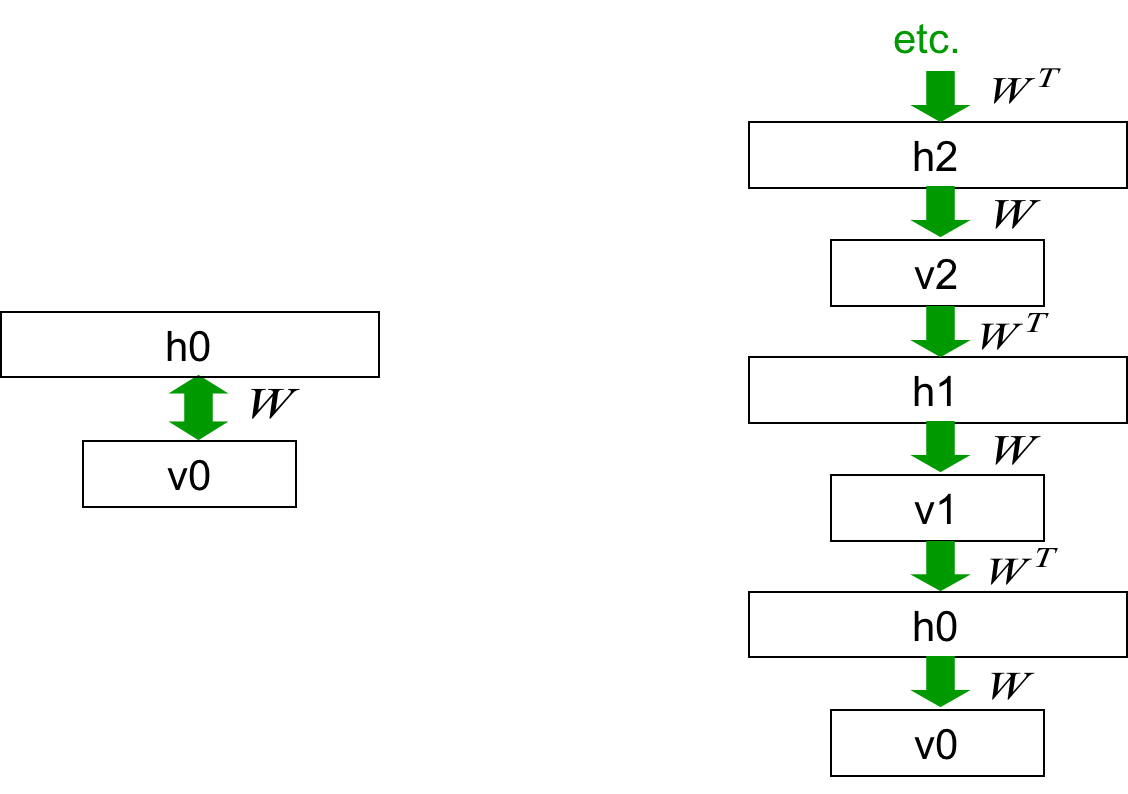
双向箭头可以看做是无限层叠的缩写，然后用CD1而不是最大似然去学习这个“RBM”。
接着将第一个W“冻结”（固定，不让其变化）住，剩下的权值依然绑在一起。就好像把h0作为数据学习RBM一样：
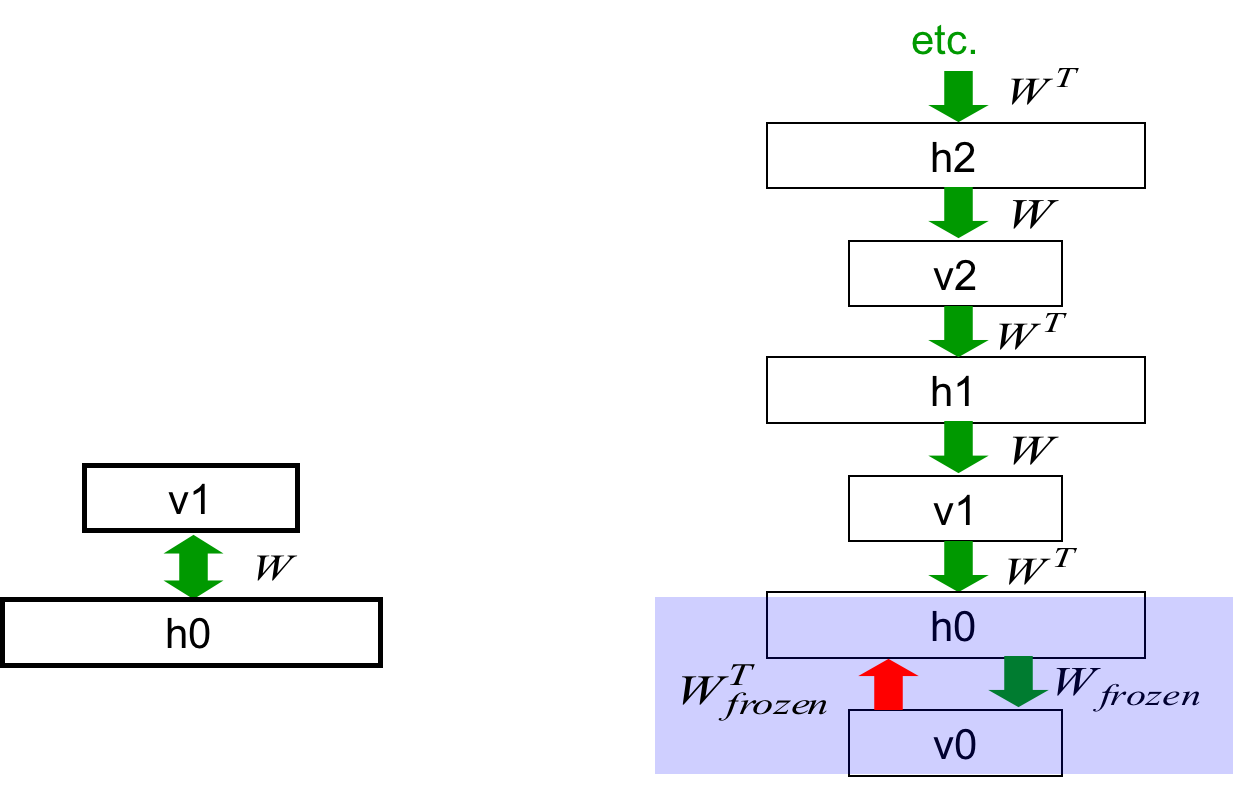
重复这个过程多次，一直到达顶层。
当上层权值与下层权值不同时会发生什么
上层不再提供精确的complementary prior的话，从下层推断的后验概率就不准确了，但提供了概率对数的variational lower bound。
但上层学习到了更接近aggregated posterior distribution的先验，使得模型输出数据的能力增强。有得有失，但Hinton, Osindero and Teh (2006) 证明了得大于失。
contrastive divergence learning时发生了什么
在这个网络中，contrastive divergence learning实际上忽略了高层网络的共享权值贡献的梯度：
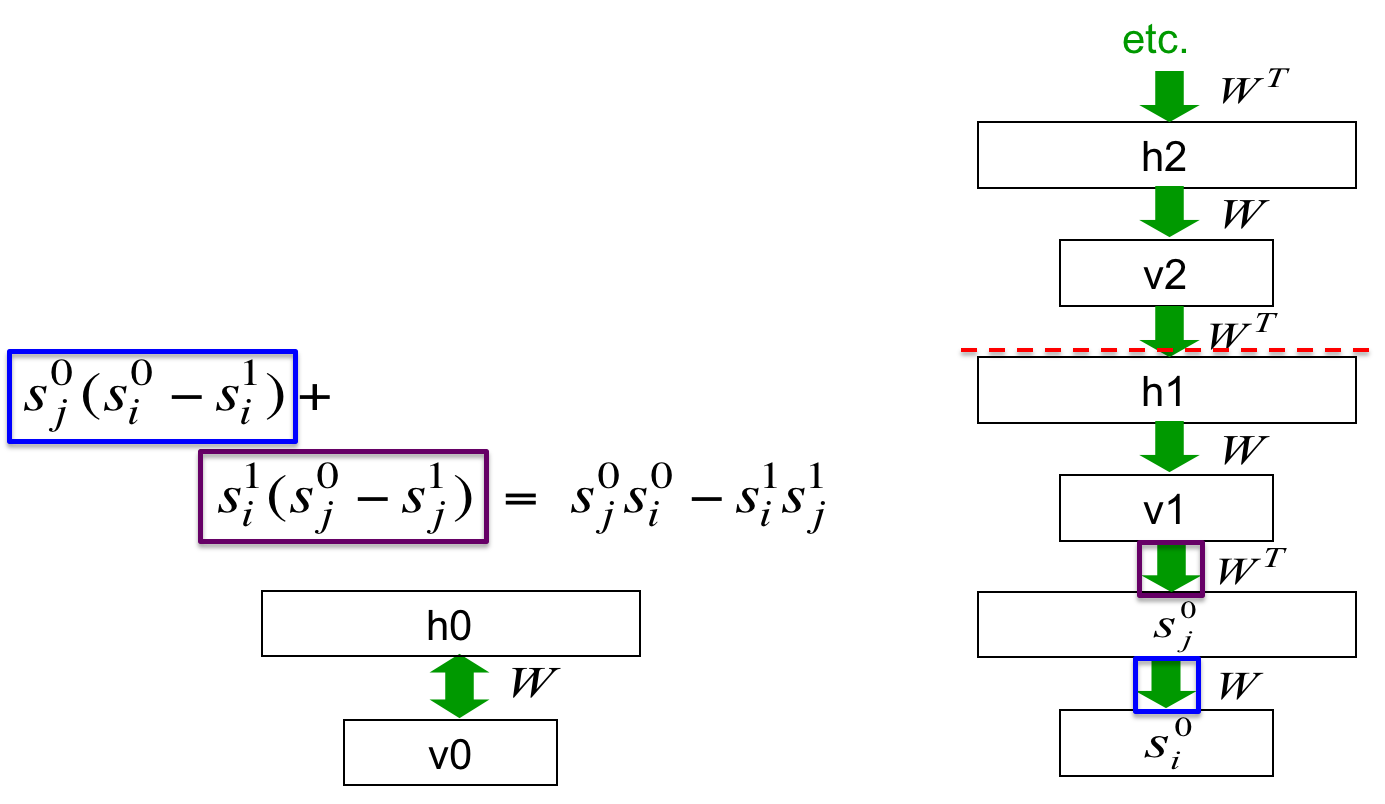
从红线处断开，上面的权值是绑定的，下面的权值是冻结的。可见第3个W的更新只涉及到前两个层，跟高层无关。
为什么可以忽略高层的梯度
当权值很小的时候，马尔科夫链mix得很快（是权值的指数函数；mix应该是这个意思：不断运行马尔科夫链到概率分布不发生显著变化）。当权值是0的时候，一步就mix结束了。mix得越多，越接近equilibrium distribution ，也就是说高层会“忘记”datavector。
在equilibrium状态时，高层隐藏单元采样自equilibrium distribution。那么数据（低层的隐藏单元）关于权值的梯度是0，因为此时的weight是对equilibrium distribution而言完美的模型。
当权值变大了之后，可能需要CD更多迭代。这对应了infinite sigmoid belief net中冻结更多层。有个有趣的结论，如果层叠RBM的目的是为了学习多层特征表达的话，那么并不一定要学习精确的最大似然，即使是CD1也能取得较好结果。
知识共享署名-非商业性使用-相同方式共享：码农场 » Hinton神经网络公开课14 Deep neural nets with generative pre-training