Hinton神经网络公开课4 Learning feature vectors for words

词的向量表示

关系信息的特征表示

引子很新奇，是一张英国人的家谱和一张结构相似的意大利人的家谱：

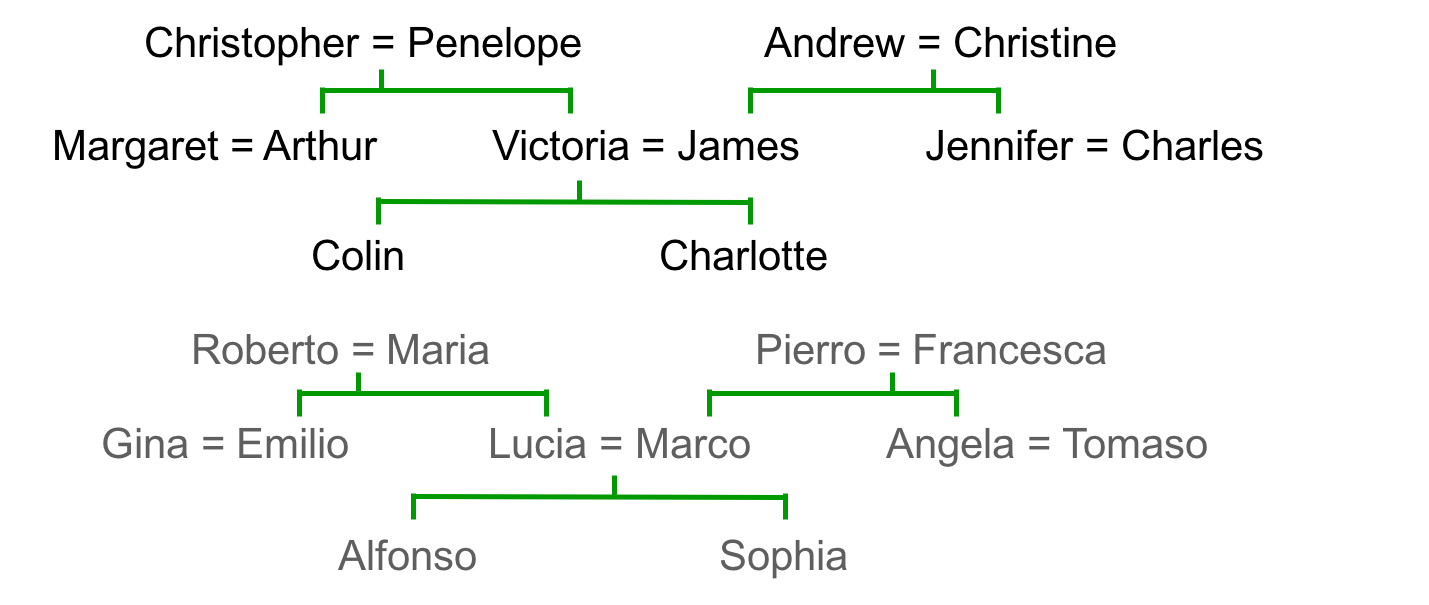
这是一种关系信息，比如甲的父亲是乙，=表示夫妻。神经网络可以通过反向传播学习这些关系对，将关系信息转为特征向量。最终的效果是，提问“乙的儿子是？”神经网络能够回答“甲”。将这两个家谱的关系对一同输入神经网络，我们还期待神经网络也能正确回答。这其实与word2vec是一样的，只不过这里是一种家谱领域上的特例而已（或者说word2vec不是个新鲜东西，原理可追溯到80年代的“关系信息表示研究”）。

朴素的方法是找到规则：

但寻找规则需要搜索不连续的概率空间，比较低效。神经网络可以用连续的权值空间捕捉这些信息。比如给定第一个词“乙”，第二个词“儿子”，根据某种向量关系求第三个词。

网络结构

既然确定了输入输出，那么神经网络的输入输出层就都确定了，中间的层需要自己灵活处理。网络结构如下：

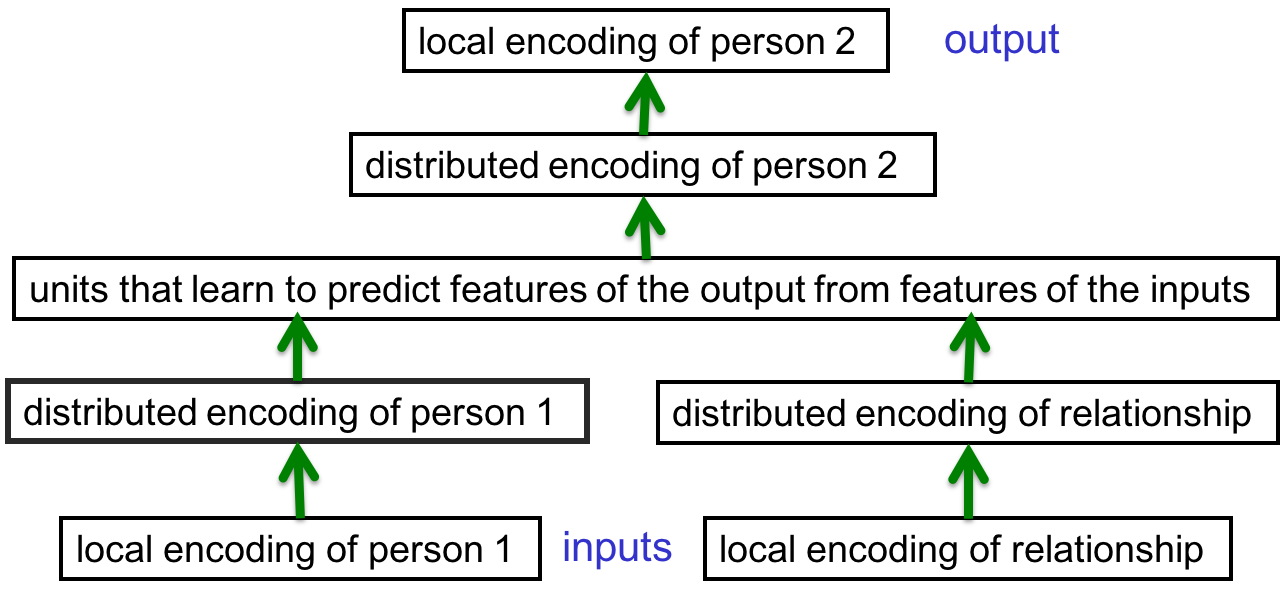
输入层是人名和关系的neutral形式，即one-hot向量。这是最原生态的特征表示，我们没有告诉神经网络谁类似谁，“儿子”类似“女儿”之类的信息。所有词语都是均等的不相似。

比如一共24个人的话，person1这层有24个输入unit。到了distributed encoding层，节点数目相对少一些，比如只有6个。因为它们没法一对一地对应到24个人，所以它必须用某种模式重新表示这些人。读入给定的112个关系对。训练的过程中不断调整权重，训练完后看看这六个unit是什么样子。

隐藏层捕捉了什么

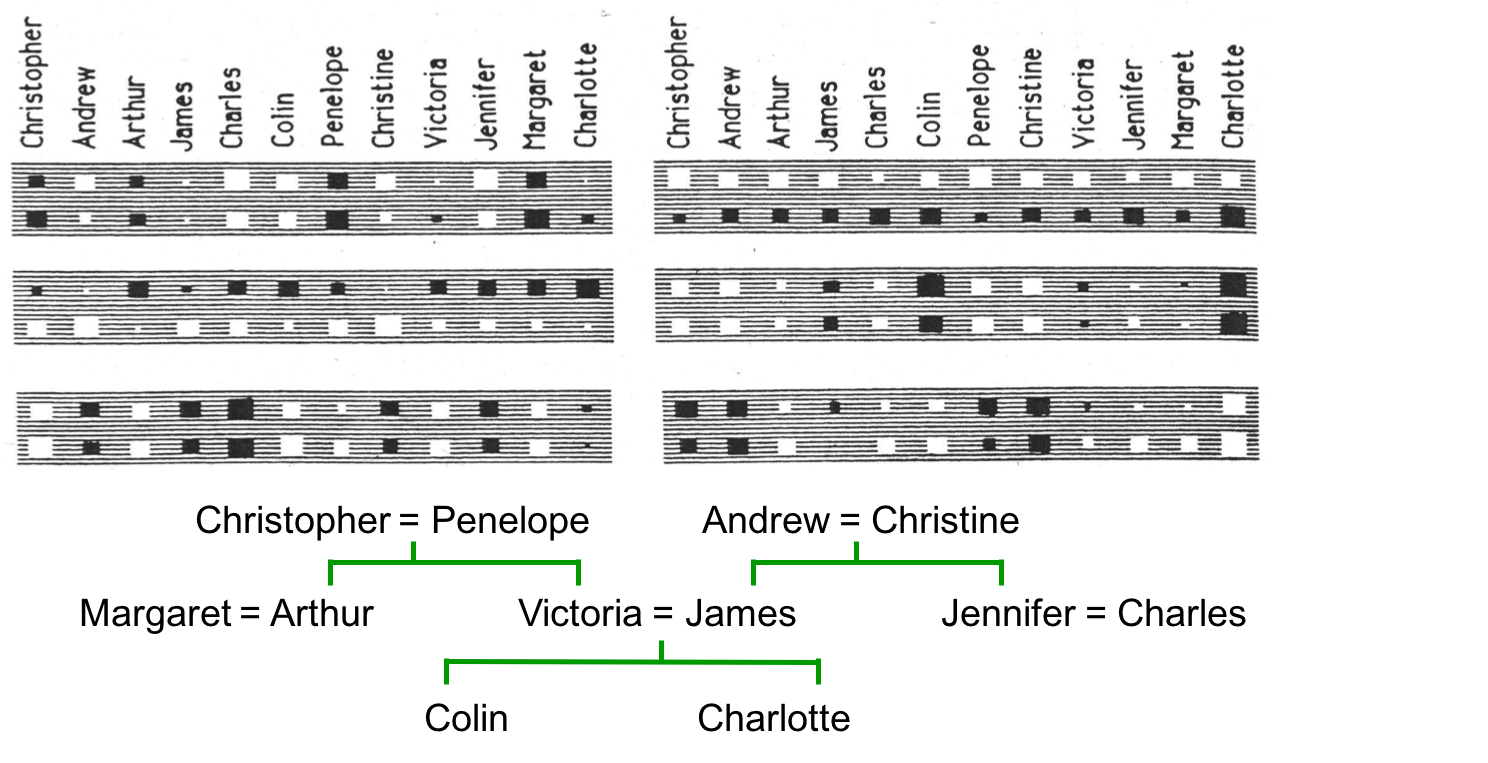
上图一共六个大长方形，对应6个unit。每个unit有24个输入，于是每个长方形中有24个小方块，分别表示该unit的输入（原文incoming weights，理解为上一级输入层one-hot向量与权值向量的element wise乘积）。白色代表正值，黑色代表负值，大小代表绝对值大小。24个方块分为两行，第一行是英国人，第二行是意大利人。

来看看右上角的那个unit，有一个有趣的现象。它的输入恰好第一行都是正，第二行都是负，这恰好区分了输入是英国人还是意大利人。我们从没有教它这个知识，但它就是学会了。这是很重要的知识，因为如果输入是英国人的话，输出一定是英国人。这代表着输出的一比特信息，抓住它就成功了一半。

右边第2个unit也很有意思，头4个大白色方块分别代表(Christopher及Roberto)和(Andrew及Pierro)。它们大小相似说明这两对人分别是类似的，这个结果与家谱一致。同理其他上下大小相似的方块都说明这样的类似关系。父亲和父亲权重相同，祖母和祖母权重相同，所以这个神经元捕捉的是“这个人属于哪一代”。正得越厉害代表越老的一代，负得越厉害代表越年轻的一代。

左下角的unit同样有可理解的信息，如果你把负值对应的人名标红，你会发现他们都位于家谱树的右边：

所以这个unit捕捉的是这个人位于家谱树的哪一边，这也是个有用的区分信息。

再次强调，我们根本没有灌输任何关于人类社会中“国籍”“世代”的背景知识，但神经网络就自动判断这些特征有用，并且学习了这些特征的表示。

应用

输出层结合隐藏层学习到的特征来做出最终推断，比如“世代=3”+“答案需要上一代”=“世代2”。

即使只在部分数据（108）个上面训练，然后在剩下的4个上做测试，也能命中两三个。对这个简单的网络而言，是个不错的成绩。

这说明反向传播可以胜任（A R B）的关系信息。不但可以用来做A R ？的预测，还可以输出A R B的概率。

认知科学之争

这是学术逸话了，浮躁的工程师可以跳过。

概念到底该如何表示呢？

1、特征论：概念由一系列特征表示，便于解释概念之间的相似性、便于将概念表示为向量。

2、结构主义论：概念不是孤立的，是关系图谱中的一个节点，由与其它概念的关系决定。Minsky将感知机的不足作为论据反驳特征论，支持结构主义论。

老爷子认为两者都不对，神经网络可以利用特征向量构成关系图谱。注意，神经网络并没有构造显式的关系图谱或在关系图谱上做显式的推断，而只是将特征一级级传播。

有些人将神经网络想象为一张关系图，每个节点代表一个实体，每条连线代表一种二元关系（父子、夫妻）。事实上这是错误的，神经元之间的权值只代表强度，不代表关系。另外，现实世界中的关系也不限于二元，有可能是多元的，比如A处于B和C之间。

目前依然没有关于“如何表达概念”的定论，但很可能的一种是，许多神经元表达一个概念，一个神经元同时参与很多个概念的表示。这种多对多的表示被称为“distributed representation”。

softmax

squared error的弱点

其一；如果目标值是1，输出很小是0.00000001 的话，那么logistic unit几乎没法得到训练。根据求导公式：

导数几乎为0，权值无法得到多少更新。

其二；输出概率没有归一化。

改进方案是使用softmax强制输出表示一个概率分布，然后使用不同的损失函数。

softmax

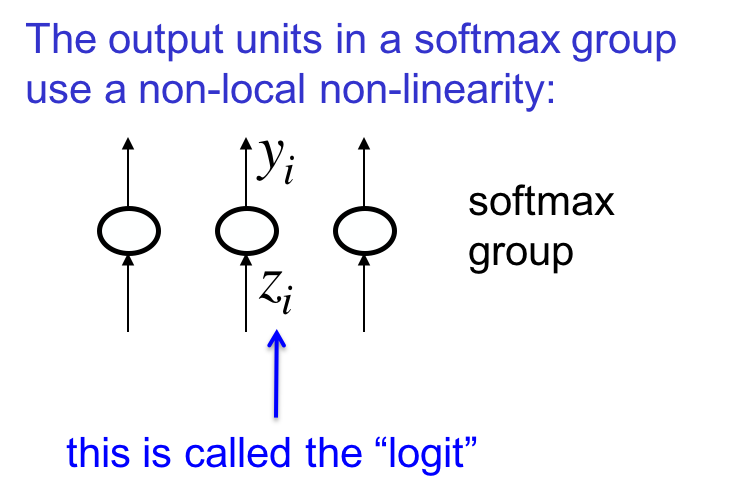
softmax单元的输出并不仅仅取决于输入z_i，而取决于整个分组的输入：

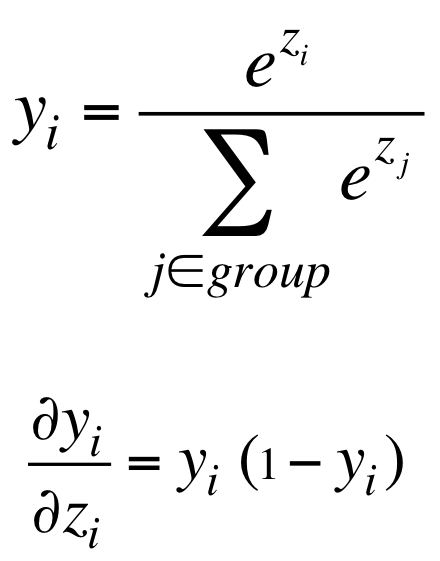
损失函数

right损失函数定义为所有unit输出right的概率的负对数（同理可定义wrong损失函数）。

其中target value仅在输出正确的时候取1，C又称cross-entropy。

所以最小化损失函数就是最大化所有节点输出正确值的概率。

这个损失函数的优点是，在目标值为1，而输出值为0的时候，梯度非常大：

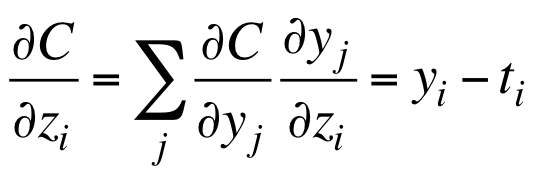
这解决了squared error损失函数的问题。而当目标值与输出值几乎相等的时候，梯度接近0，模型不发生改变，这也是我们所需的。

语音识别中的应用

我们听到we wreck a nice beach的时候，大脑下意识地输出“we recognize a nice speech”。这说明我们是在利用类似的发音对应类似的词语，并且能判断两个句子谁的概率大，也就是能预测接下来出现的词语。

旧方法

旧的语言模型是trigram模型：

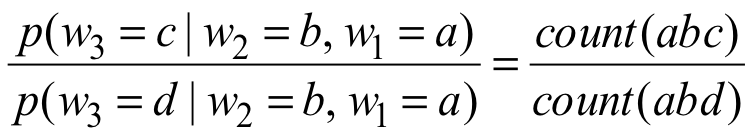
ngram模型受限于计算复杂度，n不可能太大。另外，受限于语料，平滑问题很严峻。这些传统的语言模型不理解词语之间的相似性。

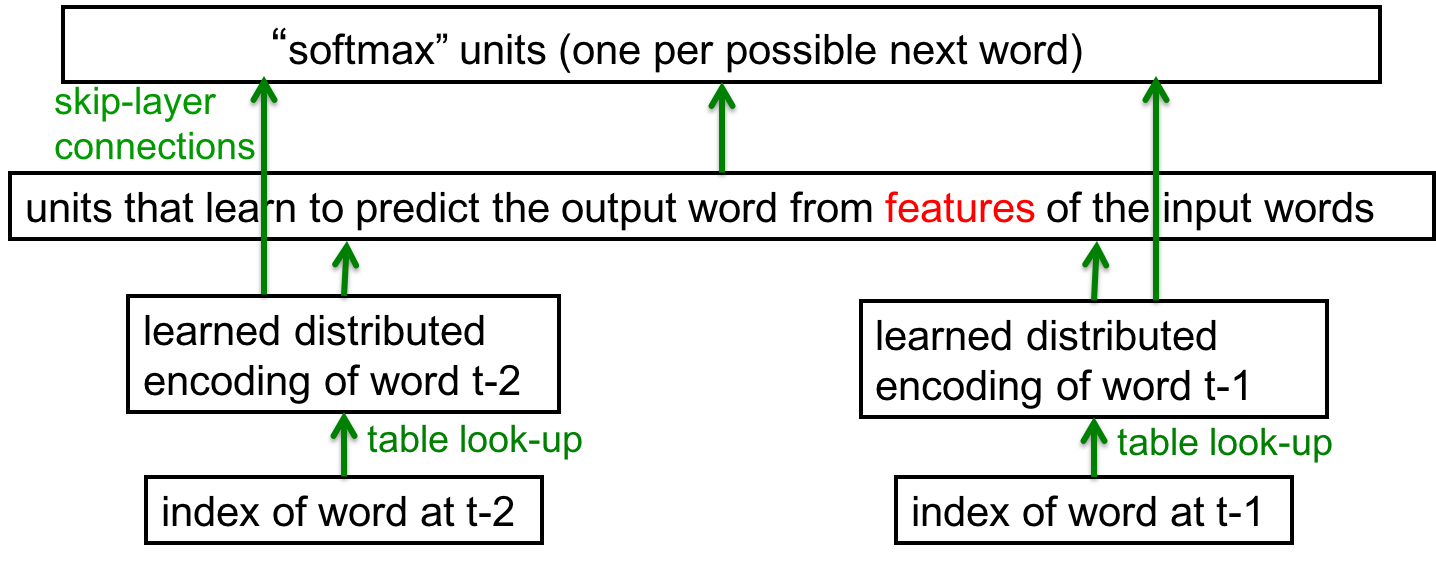
神经网络语言模型

通过词的向量表示，神经网络语言模型可以利用更大的上下文和更丰富的语义信息。一个典型的网络结构如下：

十万词灾难

如果词表太大，最后一个隐藏层会有十万个输出权值，太昂贵了。如果用小一点的隐藏层，则这些输出概率会呈现相关性，并且都很小。下一节会讲解如何解决这个问题。

解决海量输出问题

序列架构

探针法，输出层不再一下子输出十万个词语对应的概率，而只输出待检测的词语对应的概率。

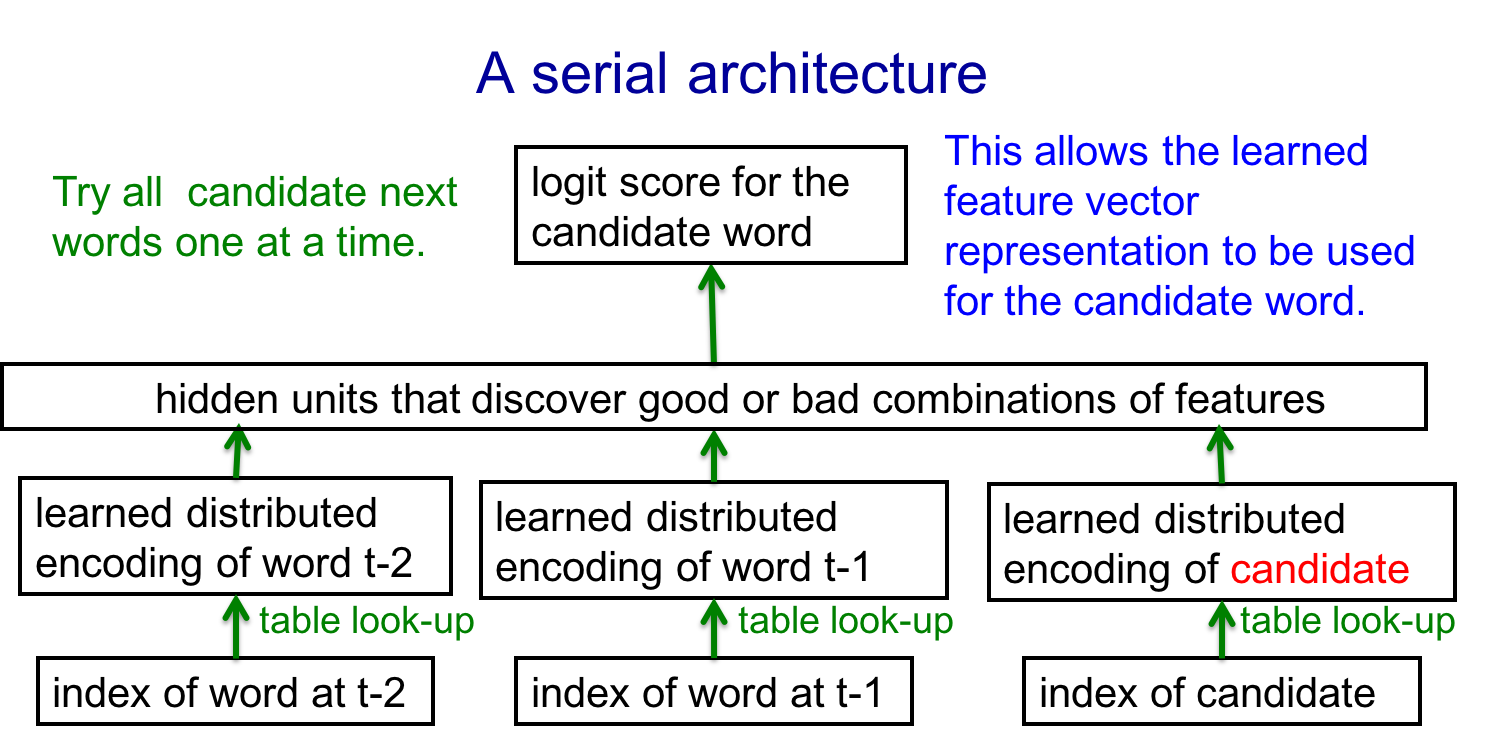
训练方法

• 计算所有候选词的logit score，代入softmax得到概率

• 计算cross-entropy，利用导数更新weights

• 如果有其他predictor提供的小集合的候选词的话，可以省下很多时间

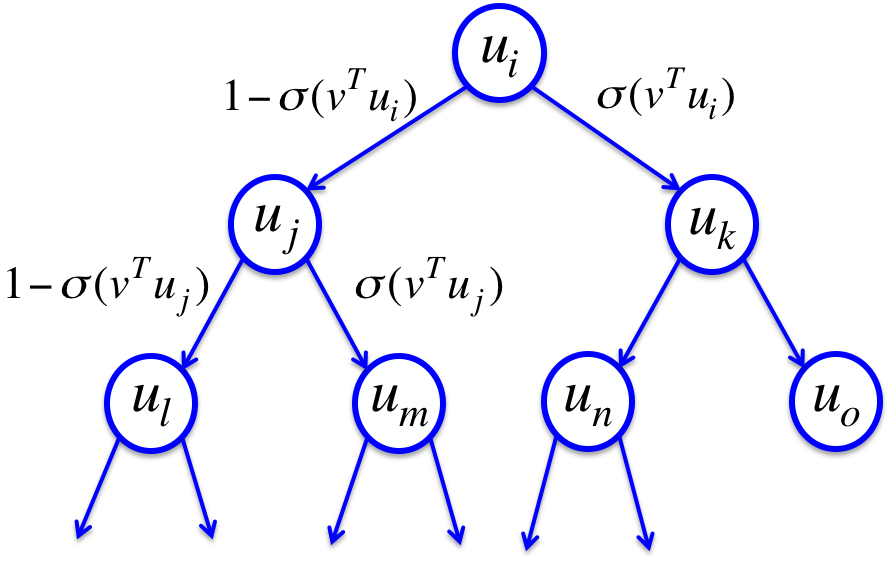
二叉树法

另一种避免十万词灾难的方法是利用二叉树将词语二进制编码

预测

预测方法是利用上下文得到一个预测向量v，与通往正确单词的路径（红色）上的所有节点的对应的向量u作比较：

训练

使用类似的网络得到预测向量v，于是走了下图红色路径：

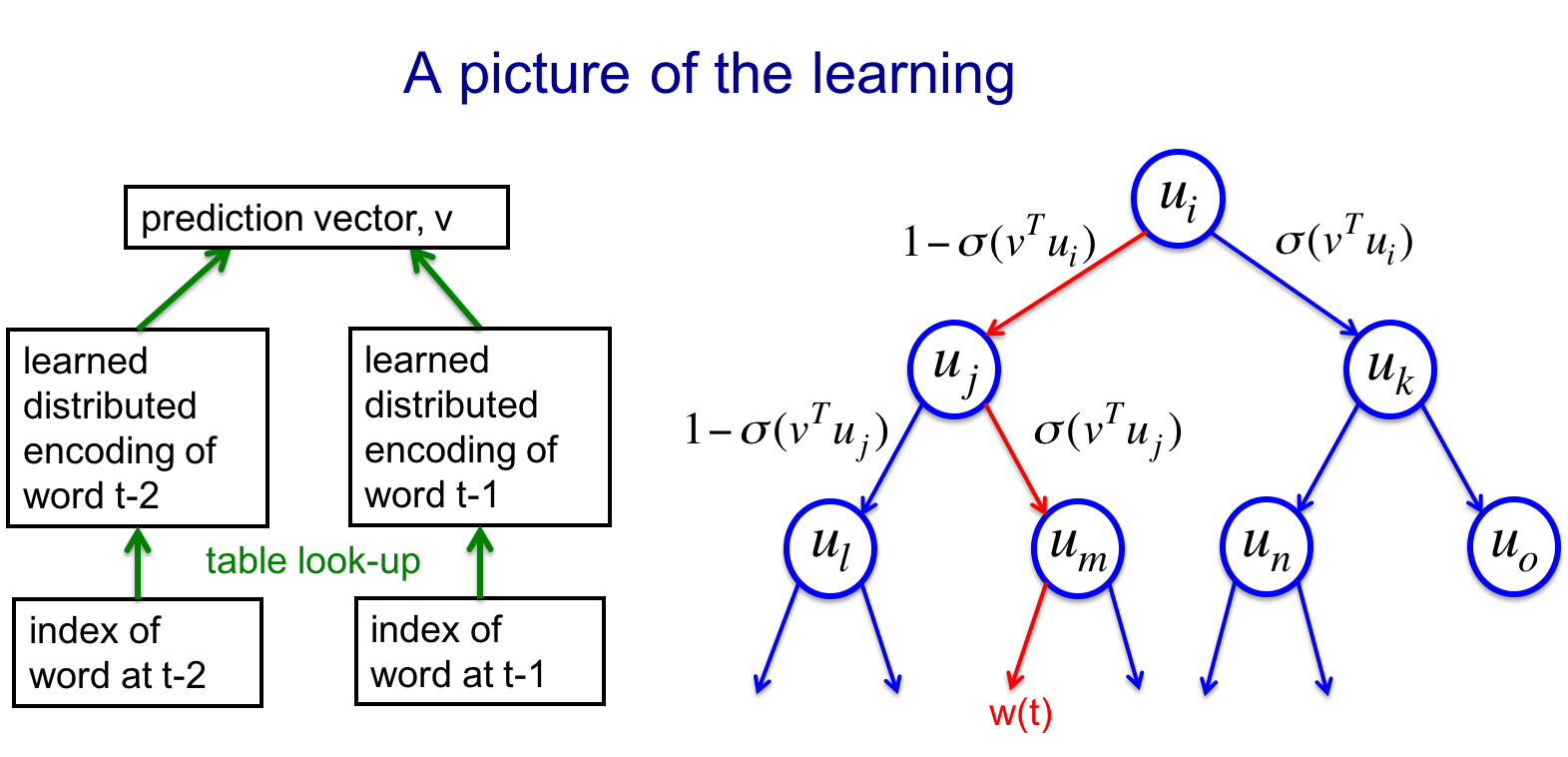
将损失函数定义为w(t)=这些路径的概率的负对数。所以训练的时候只需考虑路径上的有限的log（N）个词语，而不是全集N个词语。并且我们同时得到了prediction vector和node的vector。

但实际上依然很慢，只快了100来倍。因为在预测的时候，还是需要做十万次“探针”。

sliding window法

另一种方法利用了滑动窗口，那就不是预测下一个词了，而是预测中间的词语。输出层要么是正确的词语，要么是一个随机的负例词语（负采样）。这种方法得到的向量效果非常好。

可视化

高维词向量的降维一般用t-sne，下面是一些可视化效果：

关于体育的：

关于地名的：

其他同义词：

 知识共享署名-非商业性使用-相同方式共享：码农场 » Hinton神经网络公开课4 Learning feature vectors for words