Hinton神经网络公开课2 The Perceptron learning procedure

这是多伦多大学Professor Geoffrey Hinton的Neural Networks for Machine Learning公开课笔记，只记录难点，我已经掌握的知识点则不做记录。

Weight space

通常讲解感知机的时候，都是将实例看做多维空间上的一个点，点的坐标为对应的特征向量(data space)。但这里没有进行特征向量->点的转换，而是进行了参数向量->点的转换（weight space）。

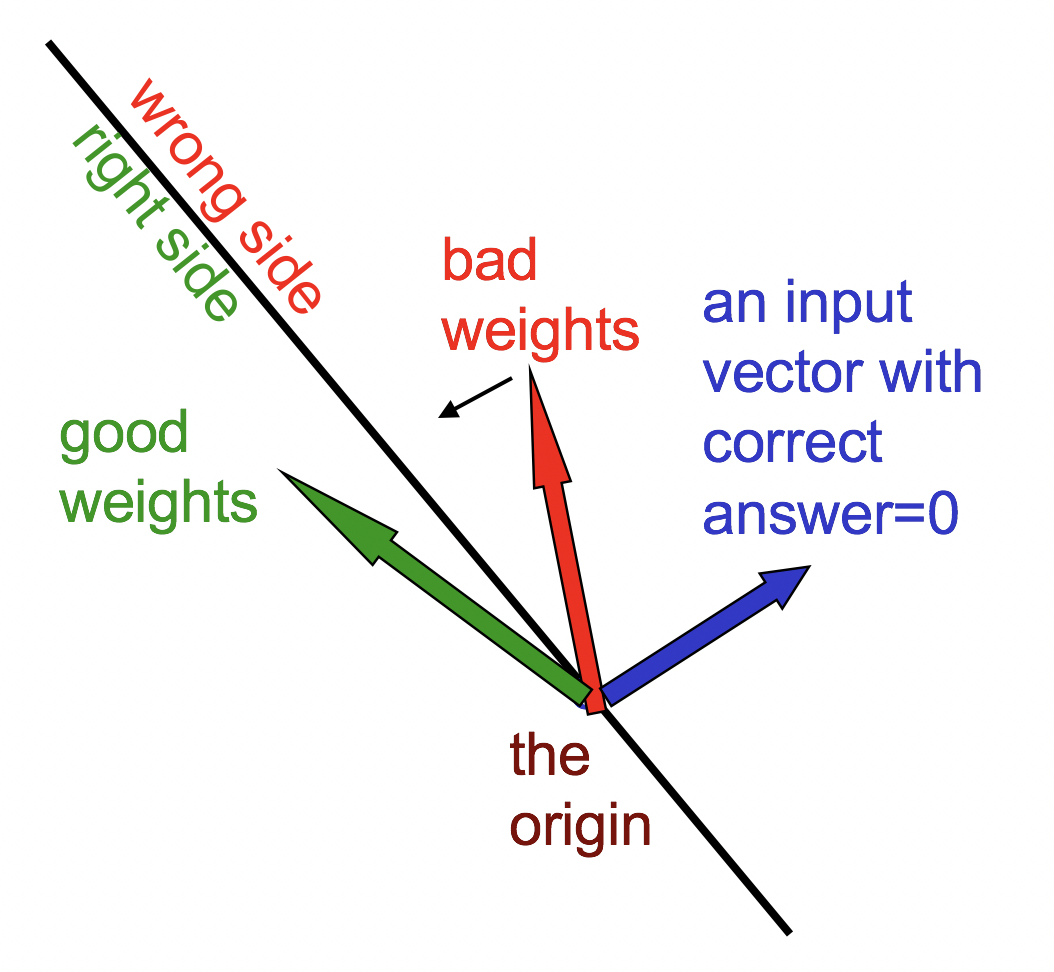
首先理解上图的前提是，要明白特征向量的维度与参数向量、weight space的维度是相同。在weight space中，每个点与原点对应一个确定的参数向量（在下文中，为了表述方便，参数向量指的就是weight space中的一个点）。

先有某个训练实例蓝色的特征向量，将其作为法线确定一个黑色的超平面。超平面对应的向量乘以法线向量等于0，说明落在超平面上的参数向量会让感知机输出0，临界条件很难决策。超平面将空间分为两个部分，落在某一侧的参数向量一定输出错误结果，另一侧输出正确结果（具体来说，y=1时与特征向量在同一侧的参数向量一定输出正确，y=0时与特征向量在不同侧的参数向量一定输出正确）。

每个训练实例对应一个超平面，感知机训练算法就是要找出这些超平面分割出来的一个“夹角”内的某个参数向量。该向量能使感知机对所有训练实例都输出正确结果（至少尽量多的实例）：

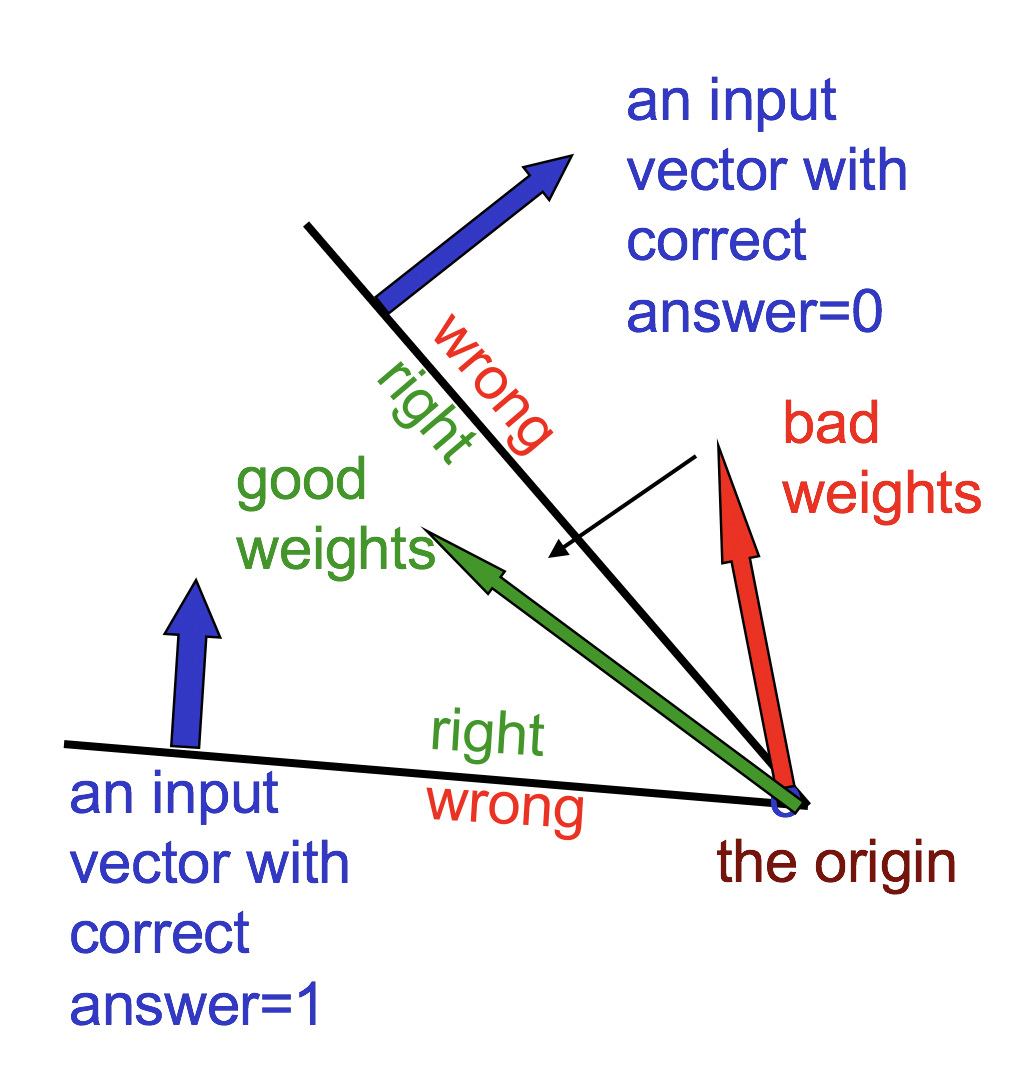
如果两个参数向量是可行，那么夹在它们中间的那些向量一定也可行，说明这是个convex问题。

为什么感知机算法可行

感知机参数向量v训练算法很简单，对任意训练实例(x,y)，其中y=1或0，假设特征向量为f：

若y=1，则v += f

若y=0，则v -= f

形象地说，就是data space中weight plane朝着误分类点移动：

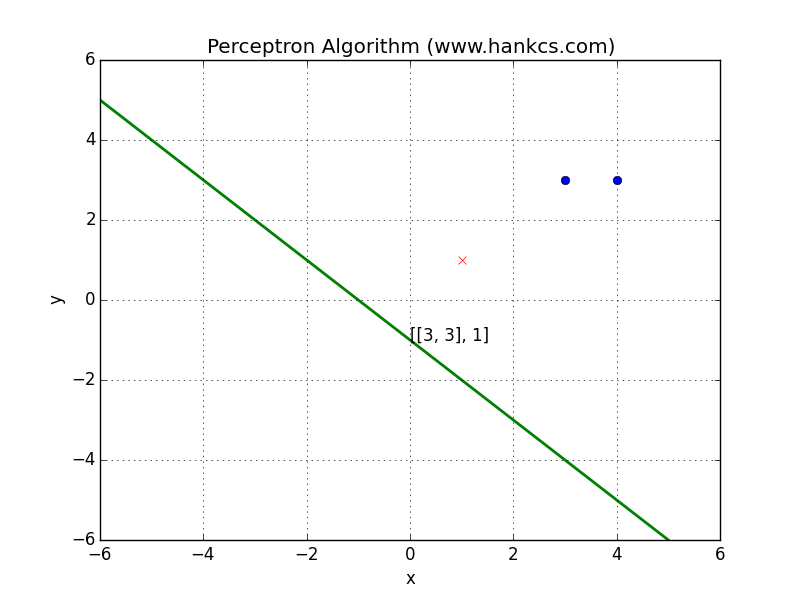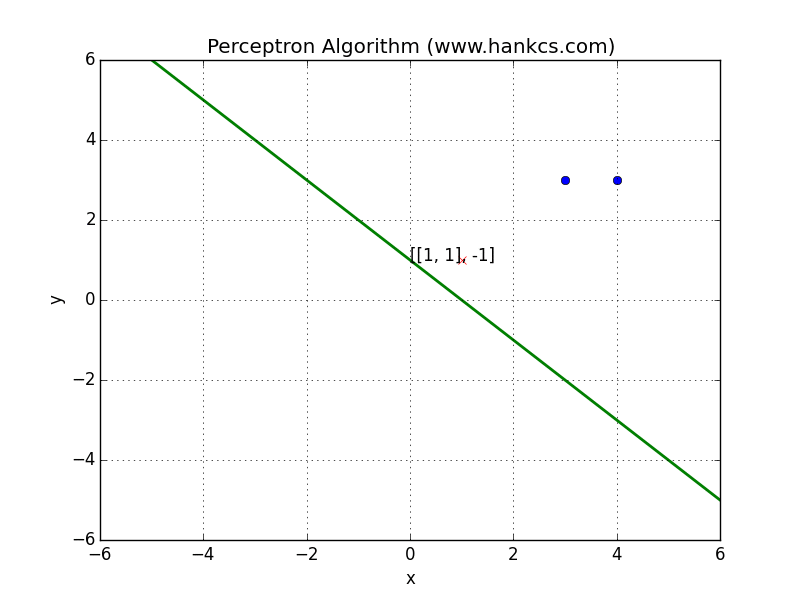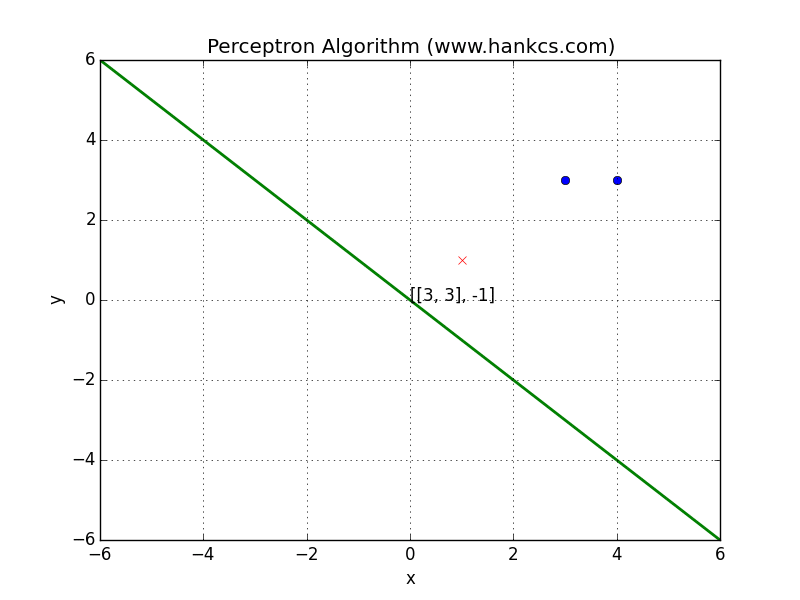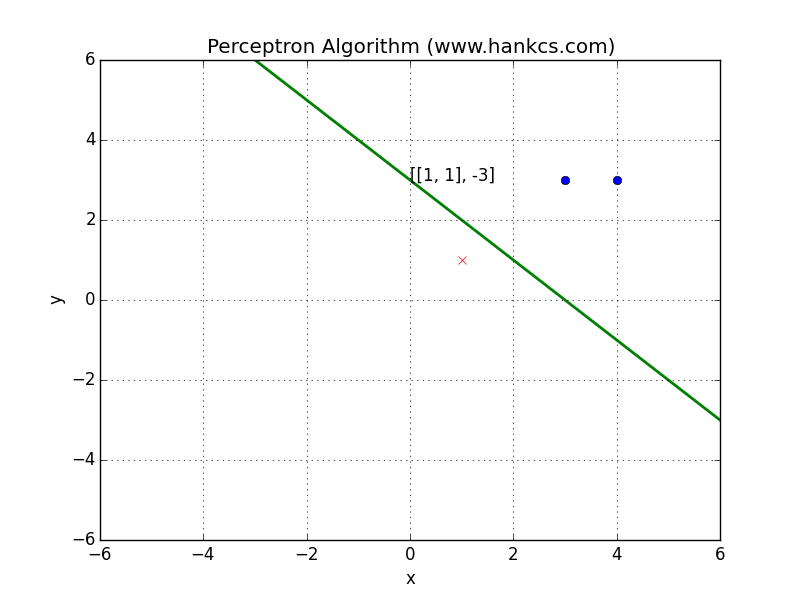
在weight space中的解释如下

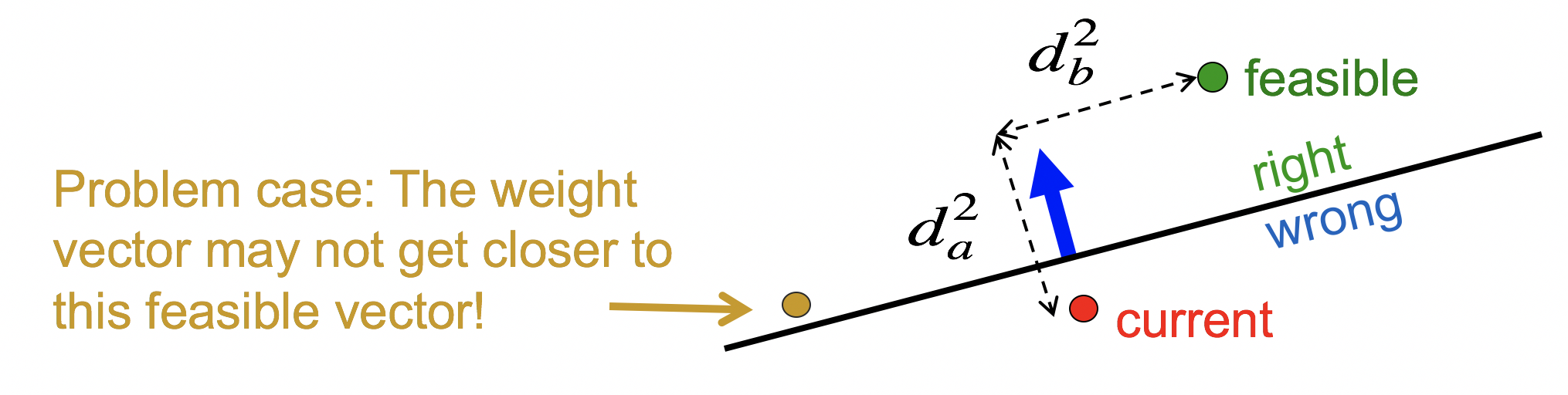
假设绿点为最优的参数向量，红色为当前参数向量，蓝色为特征向量。训练的目标是让红色点尽量接近绿色点，定义目标函数为两者的squared distance。

如果不加限制地随意移动的话，有可能得到新的参数向量橙色点，遗憾的是，虽然橙色点位于正确的一边（是可行的），但离绿点的距离更远了。所以我们需要一个限制，将橙色点排除在外。定义margin=特征向量的长度，限制可行解离超平面的距离必须大于等于margin。于是可行解不再是实线上面的部分，而是虚线上面的部分。

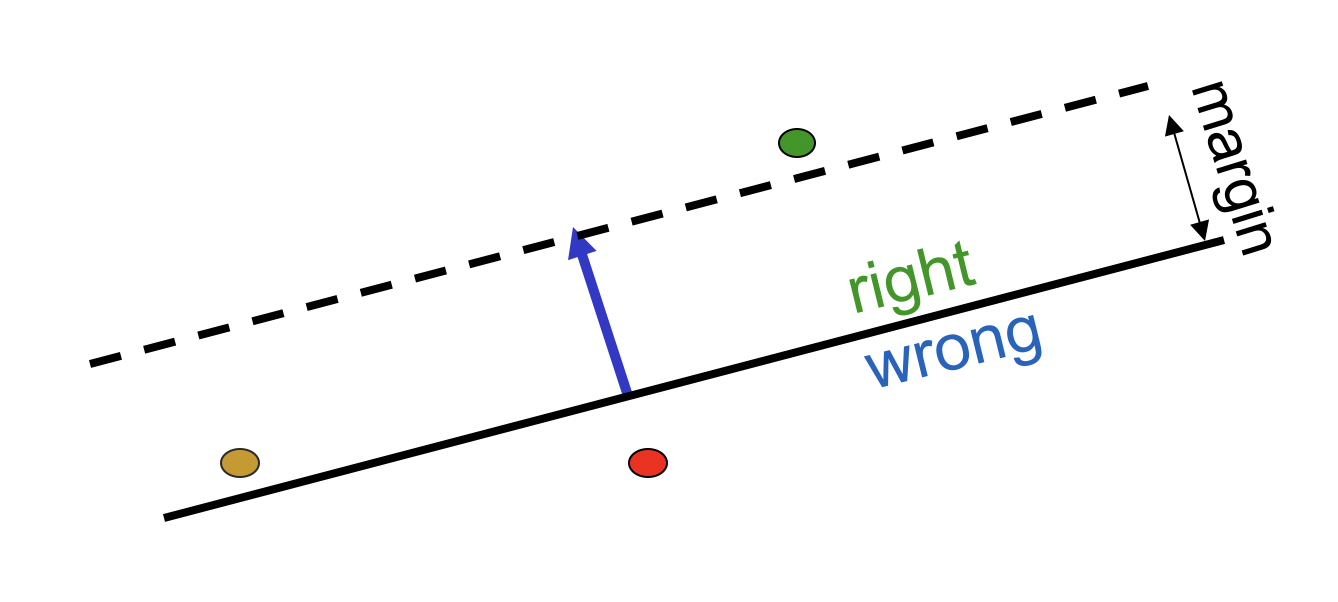
于是就把橙色点排除了。

由于y=1，我们执行v += f，使得红色点沿着蓝色向量移动与其长度等长的距离，square distance恰好减少特征向量长度的平方那么多。由于每次移动离实线的距离都减少了margin，所以总会在有限次移动后到达距离实线margin开外的区域（如果该区域存在）。这个证明怪怪的，老爷子表示你们数学系的肯定有形式化的证明，但我更关心工程上的事情。

感知机的弱点

如果特征选得好，感知机几乎可以做任何事情。但如果特征选得不好，造成数据看上去线性不可分，那么感知机就懵逼了。

比如将一个XNOR门的真值表作为训练数据：

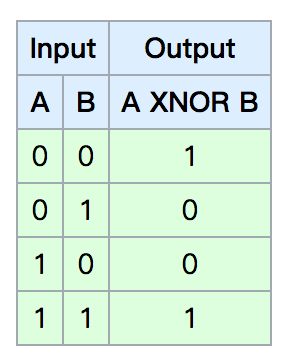
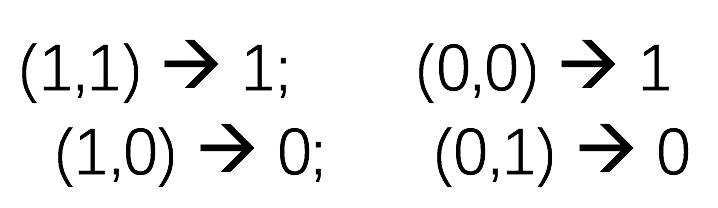
得到参数向量必须满足的方程：

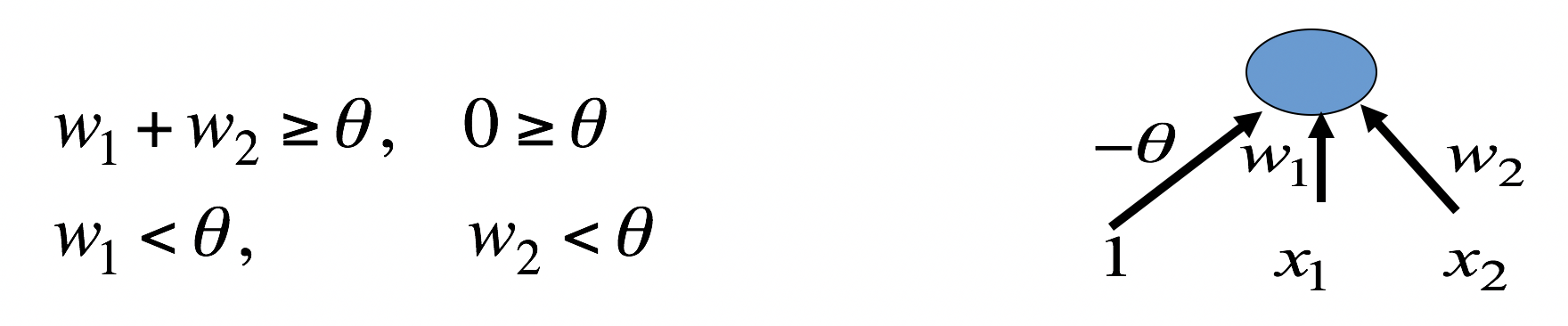
把1和2加起来得到w1+w2>=2theta，把3和4加起来得到w1+w2<2theta，无解。

如果我们将数据放到data space中，会得到如下图像：

data space与weight space恰好是对称的关系，在data space中，数据是点，weight vector对应经过原点的超平面。由于一定经过原点，所以无法区分这四个点。

另一个例子是n*1的图片的模式识别，两种模式分别只有4个像素是黑色，其他都是白色。

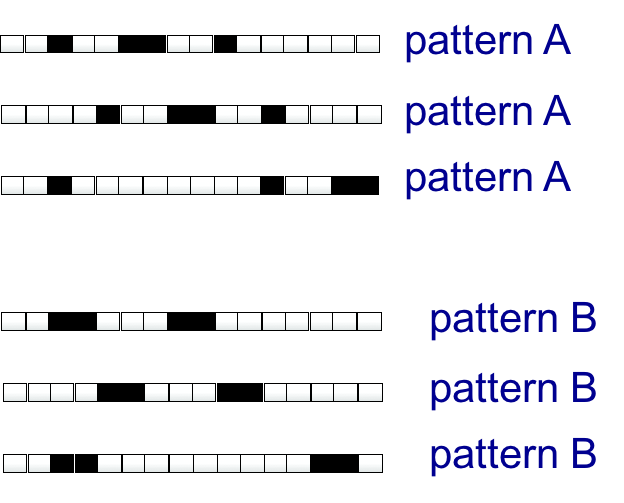
假设在所有可能的rotate transform上训练binary threshold unit，每个像素位置有四种transform是黑色（虽然上图对每个pattern只举了3个例子，但实际上有更多）。假设每个黑色像素对应1，白色对应0。那么unit在pattern A的所有可能的训练实例上得到的输入是4倍的weight向量。有趣的是，unit在pattern B上得到的输入也是4倍的weight向量。既然输入都是一样的，那么unit就无法区分它们了。详细展开说，每次迭代后，特征向量每个维度上增加和减少的总量相等，也就是不发生变化，也即是无法训练。

由于模式识别很关键的一点在于识别同一个pattern的不同transform，所以单个感知机unit不适合学习模式识别。

但如果你手工选取有效的特征的话，感知机框架仍然有效。比如增加一些feature unit识别sub pattern。所以感知机模式识别的关键在于手写特征detector，而不是机器学习。老爷子说这个弱点被过分解读，导致早期很多人认为感知机不好用，那么神经网络也不好用。

如果有办法训练特征识别模块的话，神经网络就好用了。我们不但要学习特征权重，还要学习特征表示。第二代神经网络其实全是关于特征表示的学习（早期的神经网络没有hidden unit层，特征是原始的）。

多个线性的隐藏层无济于事，整个模型依然是线性的。于是怎么有效地训练非线性hidden unit就成为关键问题。学习流入hidden units的weight其实就是学习feature。

 知识共享署名-非商业性使用-相同方式共享：码农场 » Hinton神经网络公开课2 The Perceptron learning procedure