码农场目录
虽然反向传播很简单，但老爷子讲的更本质。另外线性回归→逻辑斯谛回归→反向传播神经网络是很多课程的必经之路。
为什么感知机算法不能用于训练隐藏层
其实前面一次课简单地提了下，说是线性隐藏层构成的模型依然是线性的。这节课展开了讲，感知机算法的迭代目标是使得权值向量更接近“可行”的向量集合（上节课提到的虚线上方），但并不保证输出结果更接近真实结果。而复杂网络中，两个可行的权值向量的平均可能并不可行（非凸）。所以管神经网络叫multi-layer perceptrons（多层感知机）的提法是不对的。
与感知机算法的迭代目标不同，理想算法必须保证输出值更接近真实值。最简单的做法是以squared error为损失函数的linear neuron。补充点私货，这样的linear neuron其实就是线性回归：
假设函数：
损失函数：
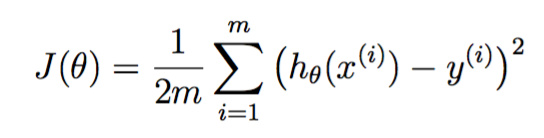
linear neuron
也称linear filters（电子领域），其实就是一条直线，也就是特征向量与权值向量的点积。
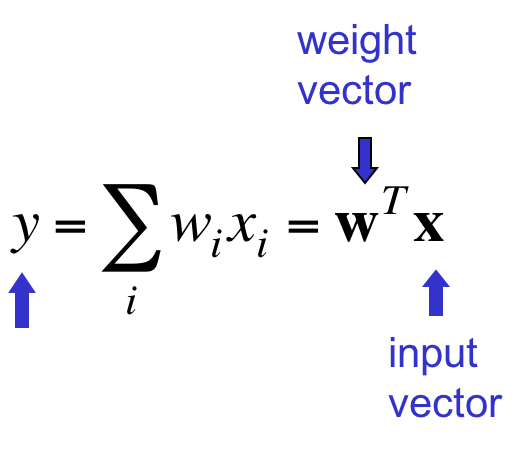
损失函数定义为上述直线方程对每个训练实例的输出与真实y的差值的平方之和。
为什么不用解析法
上述优化问题可以直接解析法解决：
但是1、我们想通过这个简单的例子模拟真实的神经元是如何学习的，它们可不会做矩阵运算；2、我们想要得出一种方法，可以推广到多层、非线性的网络上去。而解析法的前提依赖于squared error，这显然不利于推广。
迭代法解决
举个例子，假设你每天去一家餐馆吃固定的三种食物，但每次吃的数量各不相同。收银员只告诉你总价，但不告诉你每样菜的单价。
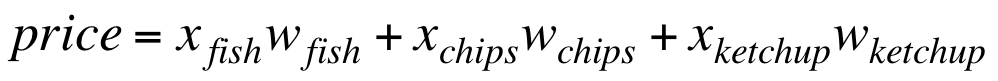
你想通过这几天积累的数据来猜出单价。
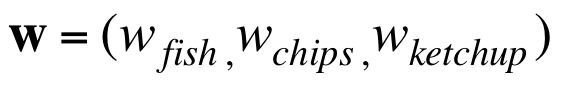
收银员的计算过程正是一个linear neuron：
开始的时候随便猜一个值，假设每样的单价都是50：
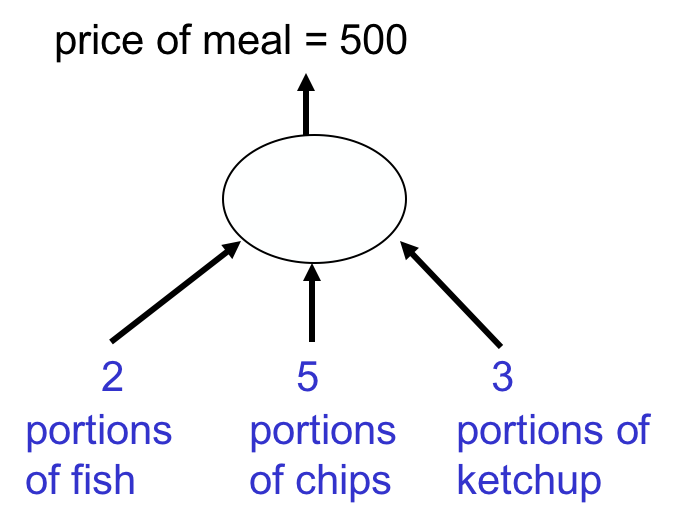
这与正确值之间相差350，使用参数更新公式（所谓的delta rule）
，取学习率epsilon=1/35，那么权值向量的更新量为+20, +50, +30。于是新的权值向量为70, 100, 80。注意chips的权重实际上变差了。
推导参数更新公式
其实就是CS229编程1：线性回归里面讲到的梯度下降：
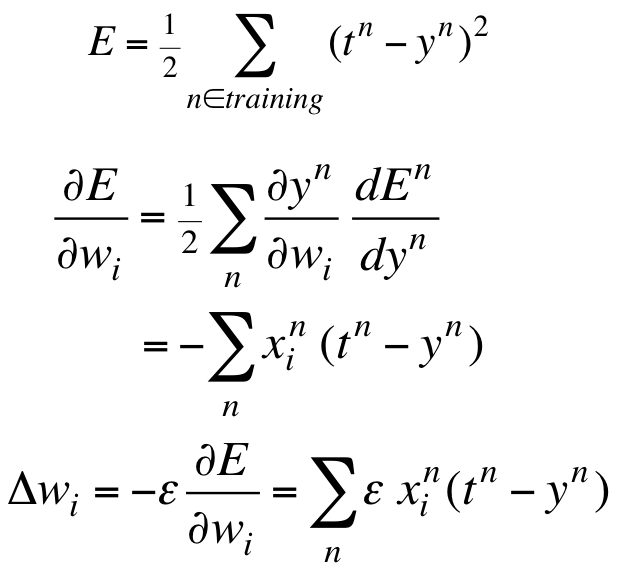
其更新公式与最小二乘法或批梯度下降算法是一致的：
略过。
迭代算法的性质
一定能得到最优解吗？
-
有可能没有最优解
-
将学习率取小一点，总可以得到符合要求的精度
算法收敛速度
如果输入数据的某两个维度紧密相关，比如总是相同的，则很难区分这两个维度对应的权重。
与感知机的类似点
如果使用在线版本的迭代算法的话，则与感知机很像，不同之处在于：
-
上一课的感知机没有学习率
-
感知机只在出错的情况下才更新权值向量，但这里每次都更新
weight space中的error surface
以误差为y轴，每个权值为x轴可以得到多个error surface。对square error的linear neuron 来讲，每个权值与误差的图像一定是下图这样的二次曲线：
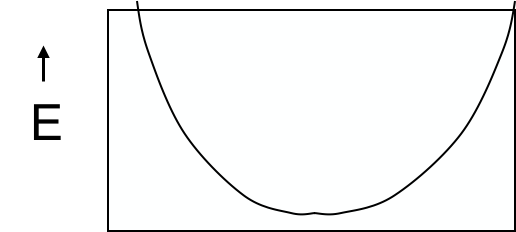
对二维的weight space来讲，则可以做出如下碗状的“等高线”：
Online versus batch learning
一张图说明问题：
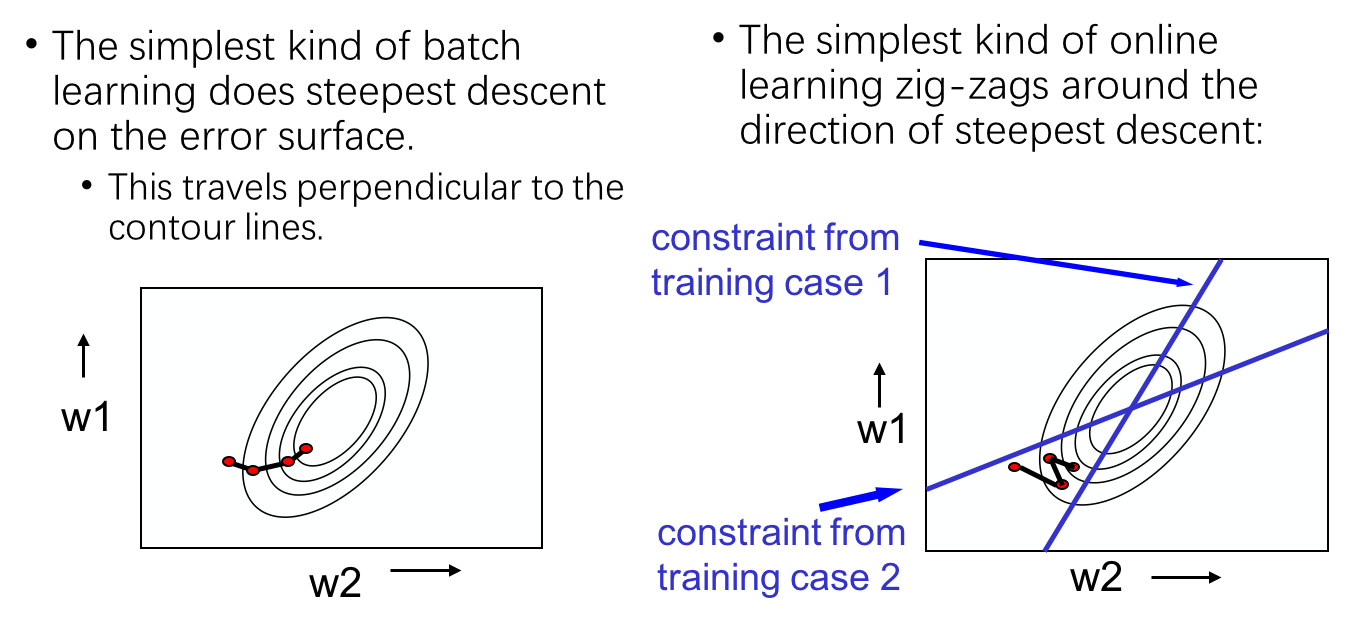
batch learning总是严格沿着梯度的方向走，而online learning并不知道梯度的确切方向，只在训练实例构成的限制线的正确一侧向着最优解z字形移动。因为它每次只知道该实例对应的梯度。
为什么训练速度可能很慢
如果两个特征维度强相关，也就是它们的权重几乎相等，那么这两个维度的权值几乎落在y=x这条线的附近：
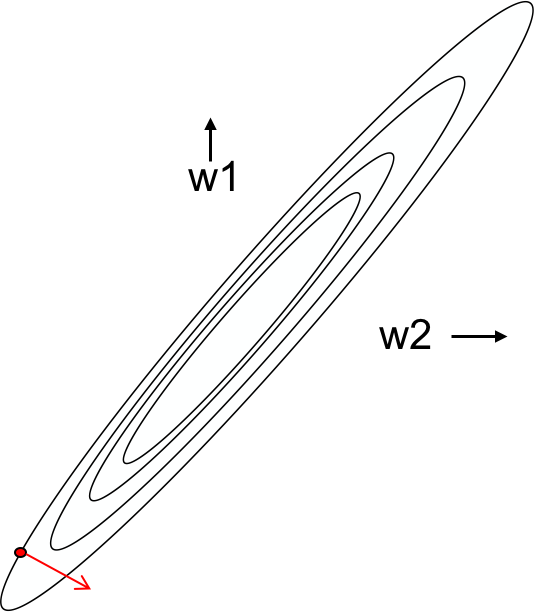
如果我们从红色点出发，会发现这一点的梯度指向了与极值点几乎垂直的方向。其在极值点方向上的分量是非常小的，所以收敛速度非常慢。
从线性到非线性
学习linear neuron只是为了引入“迭代算法”这个知识点，但它依然是个线性模型，处理不了非线性的数据。
非线性的neuron有logistic neuron。
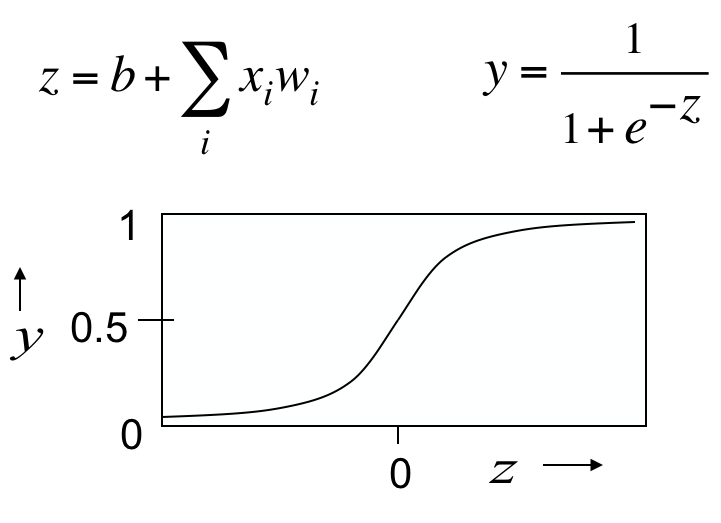
z和y的导数都非常漂亮：
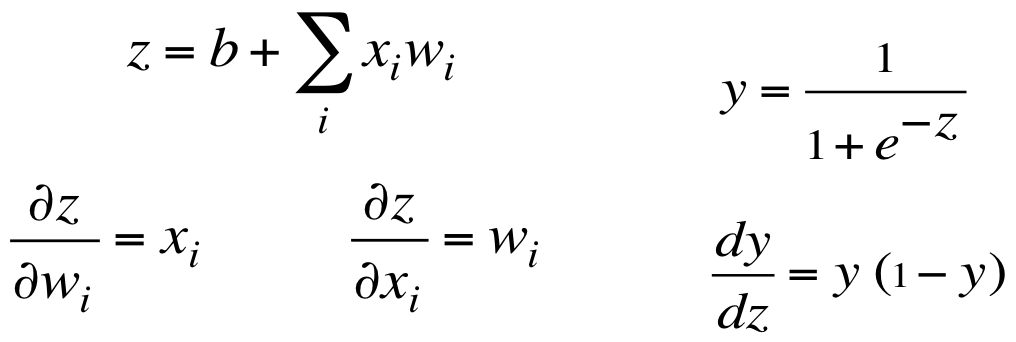
老爷子还耐心地帮我们推导了一下：
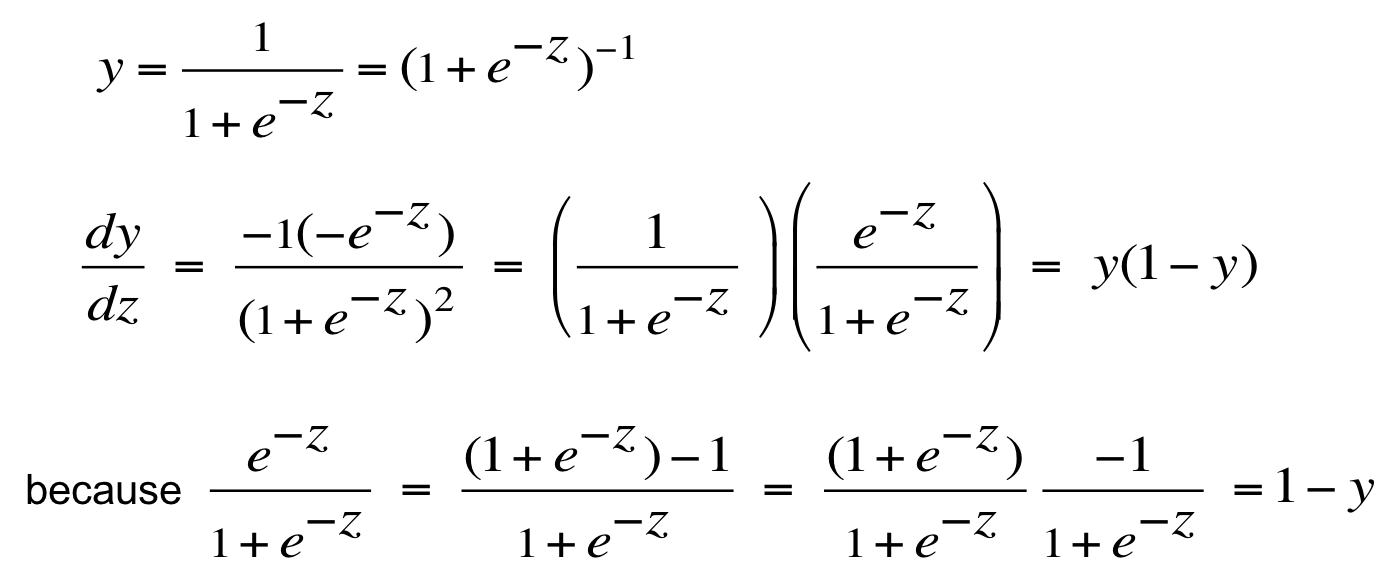
利用求导的链式法则，可以推出平方误差关于某个参数的导数：
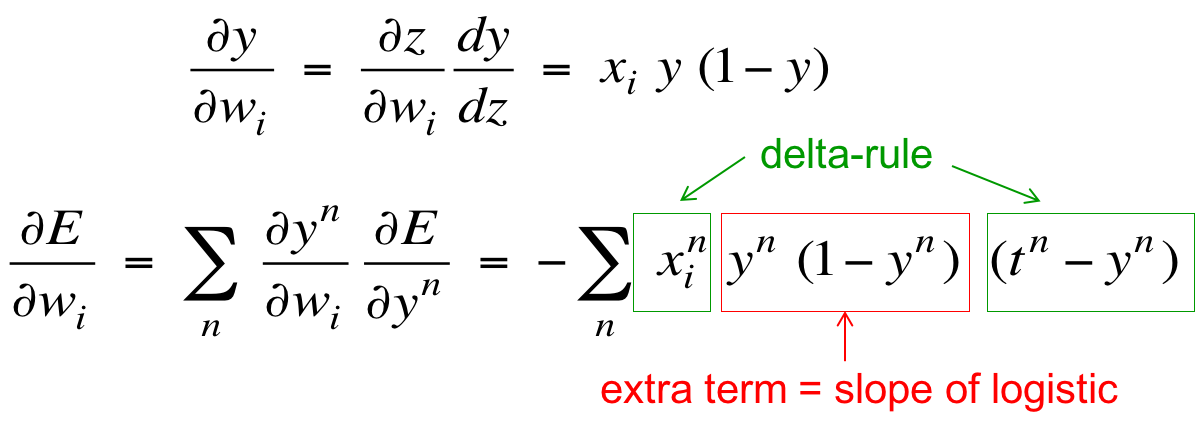
上标n表示训练实例，t表示目标值，y表示输出值。最后一个绿框来自
的导数。
从另一个角度看，绿色部分与delta rule一模一样，而红色部分是sigmoid激活函数的梯度。
学习多层特征
终于进入主题了，前面说过，可以通过人工手写feature来改进感知机的效果，但这样太累了，我们想要自动学习特征表示。
通过试探学习权重
在介绍反向传播前，有种不太实用的算法要介绍。通过随机改变某个权重，如检查误差变小，则保留此改变，如是达到最优化的目的。
-
这其实是一种reinforcement learning
-
非常低效，因为每次改变一个维度的特征，却要在所有的units上执行前向传播
-
对大的权值改变不友好
一种改进方法是同时改变所有的权重，然后检查误差变化。但这无济于事，因为所有改进都是可取的概率实际上比单个的概率更小，我们需要更多的尝试次数。
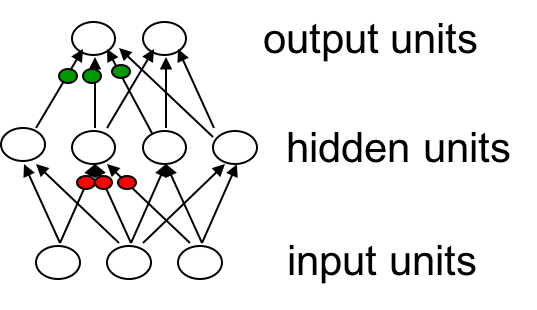
一个好点的主意是随机扰动hidden units的激活值（输入值红色），因为激活值的数量比weights的数量要少很多（有点像dropout trick，老爷子特喜欢捉弄神经网络）。
但这个主意依然比不上反向传播算法，反向传播算法不使用好的的激活值去训练隐藏层（需要所有hidden units执行前向传播才能知道某一个hidden units对应的激活值是否是好的），而是直接利用误差关于激活值的导数去更新权重。我们可以一下子高效地计算出所有hidden units的误差关于激活值的导数，接着可以很简单地求出误差关于流入hidden unit权重的导数，最终就能很高效地更新权重了。
反向传播算法sketch
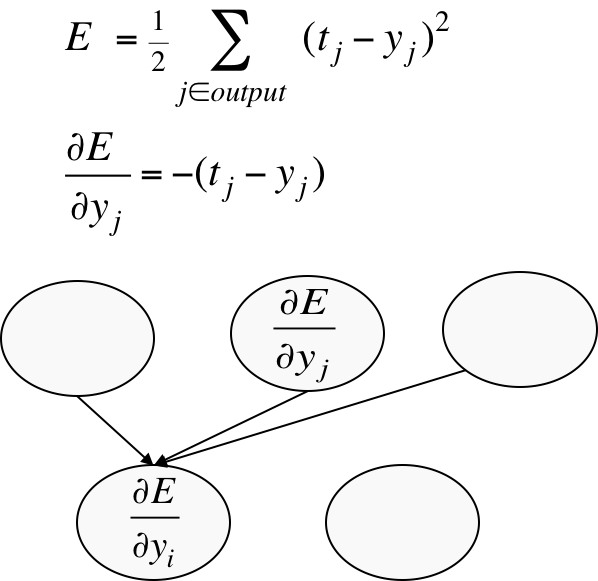
下标表示layer编号，最上面一层是输出层。从输出层开始求导，对某个hidden unit，对与它相连的output unit的导数求加权和（就像前向传播一样）。
还是用图说话吧
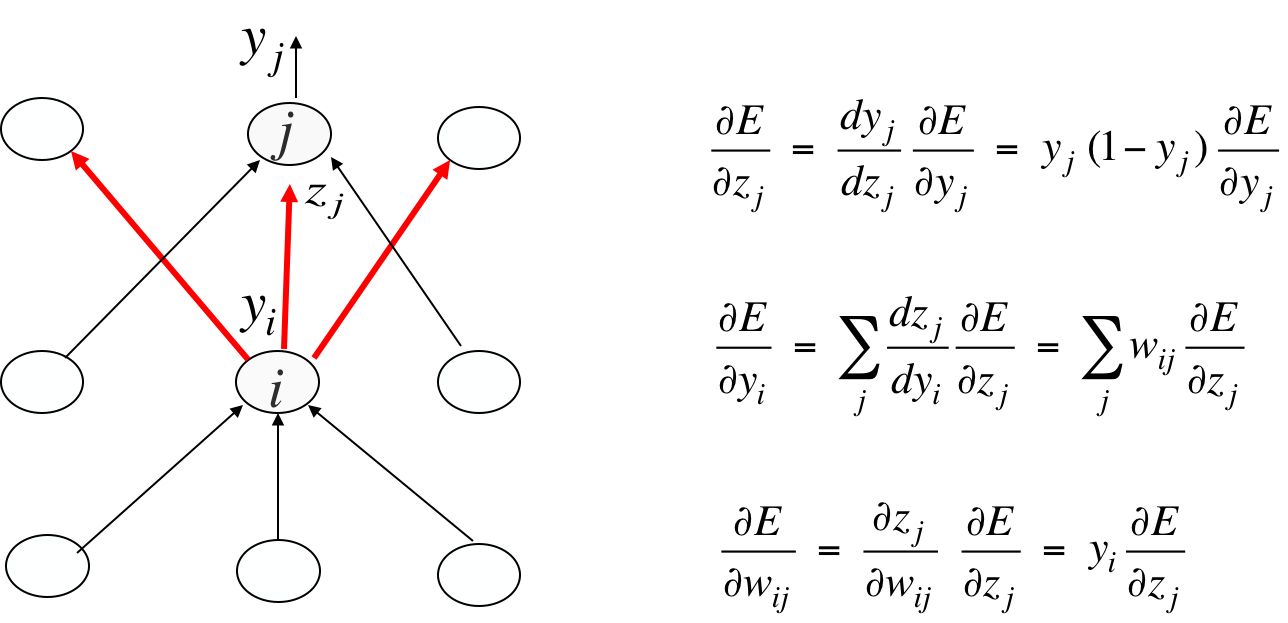
对i来说，误差关于yi的导数来自红线所连接的3个output unit。其他推导前面都有。不要被箭头迷惑，箭头是前向传播的箭头，将其反过来就是误差后向传播的方向，所以i有3个入度。
一旦有了dE/dzj，那么绿线对应的导数都是这个值：
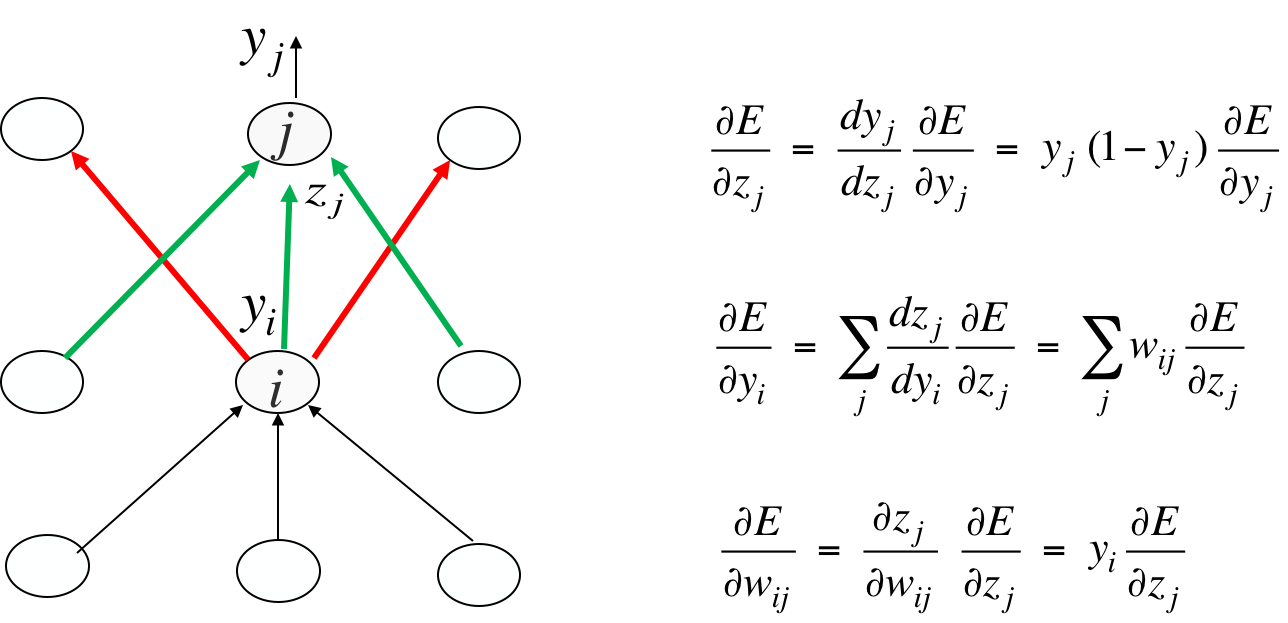
所以说反向传播很快。一旦有了dE/dyi，利用yi=zj，马上就能得到dE/dwij。至此我们就知道应该如何更新wij了，解决了需求。
接下来的课程
不过在实际应用中，还有两类问题要解决：
-
最优化问题：更新频率与幅度究竟应该为多大
频率：Online or Full batch or Mini-batch
幅度：固定学习率？ 全局学习率 ？ 每个connection分别制定学习率 ？ 不严格按梯度来？ -
泛化问题：如何防止过拟合？数据的两种噪音
数据不可靠
数据含有偶然的pattern
过拟合例子
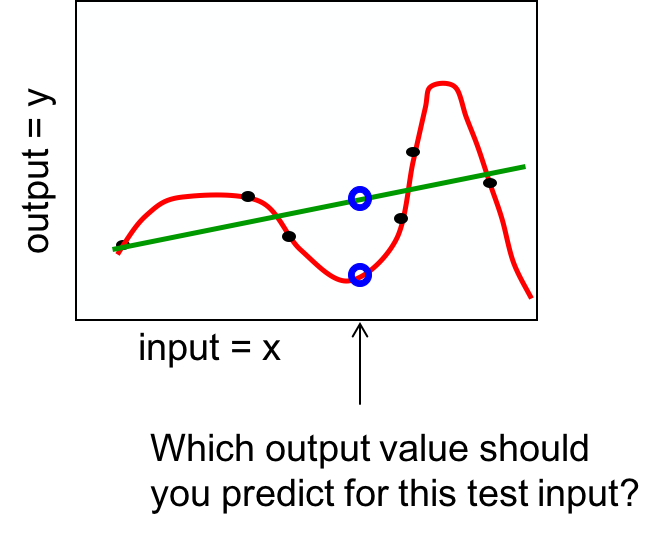
对一个回归问题，红绿两种模型哪种更可信呢？
模型越复杂拟合得越好，但越不容易泛化，越不经济。
几种减少过拟合的方法
-
Weight-decay 权重尽量小
-
Weight-sharing 尽量让多的权重相等
-
Early stopping 在开发集上性能开始变坏就终止训练
-
Model averaging 平均同一个数据集上的不同模型
-
Bayesian fitting of neural nets 另一种fancy的averaging
-
Dropout 随机扰动hidden units
-
Generative pre-training 后面课程再讲
许多知识都会在接下来的课程中讲。
知识共享署名-非商业性使用-相同方式共享：码农场 » Hinton神经网络公开课3 The backpropagation learning proccedure